PTA-7-37 整数分解为若干项之和 (20 分)

最新推荐文章于 2023-03-23 19:36:31 发布

芝士就是菜

最新推荐文章于 2023-03-23 19:36:31 发布

阅读量1.9k

点赞数 12

分类专栏： PTA刷题文章标签： c++

本文链接：https://blog.youkuaiyun.com/weixin_43691984/article/details/120066647

版权

PTA刷题专栏收录该内容

24 篇文章

订阅专栏

本文探讨了一道涉及整数分解的编程问题，通过回溯剪枝优化，解决正整数N的所有整数分解式子。关键在于设置合理的终止条件，避免超时，代码示例及优化后的AC代码展示了如何用C++实现这一过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

综述：

整数分解这题放在这个地方感觉是不大好的有点超纲，这种题常规的循环是很难完成所有正确情况的遍历的，我也是想了好久也没想到常规方法写，后来屈服了，连C都不想用了，最后用C++写了，大致思想是回溯剪枝，总体实现起来倒是不难，但是边界条件的设立，什么时候是终止条件还是挺难搞的，回溯也是递归实现的嘛，终止条件设置不好，一下就超时，下面将详细讲解本题的做法。

题目：

将一个正整数N分解成几个正整数相加，可以有多种分解方法，例如7=6+1，7=5+2，7=5+1+1，…。编程求出正整数N的所有整数分解式子。

输入格式：

每个输入包含一个测试用例，即正整数N (0<N≤30)。

输出格式：

按递增顺序输出N的所有整数分解式子。递增顺序是指：对于两个分解序列N1={n1,n2,⋯}和N2={m1,m2,⋯}，若存在i使得n1=m1,⋯,ni=mi，但是ni+1<mi+1,则N1序列必定在N2序列之前输出。每个式子由小到大相加，式子间用分号隔开，且每输出4个式子后换行。

输入样例：

7

输出样例：

7=1+1+1+1+1+1+1;7=1+1+1+1+1+2;7=1+1+1+1+3;7=1+1+1+2+2
7=1+1+1+4;7=1+1+2+3;7=1+1+5;7=1+2+2+2
7=1+2+4;7=1+3+3;7=1+6;7=2+2+3
7=2+5;7=3+4;7=7

解题思路：

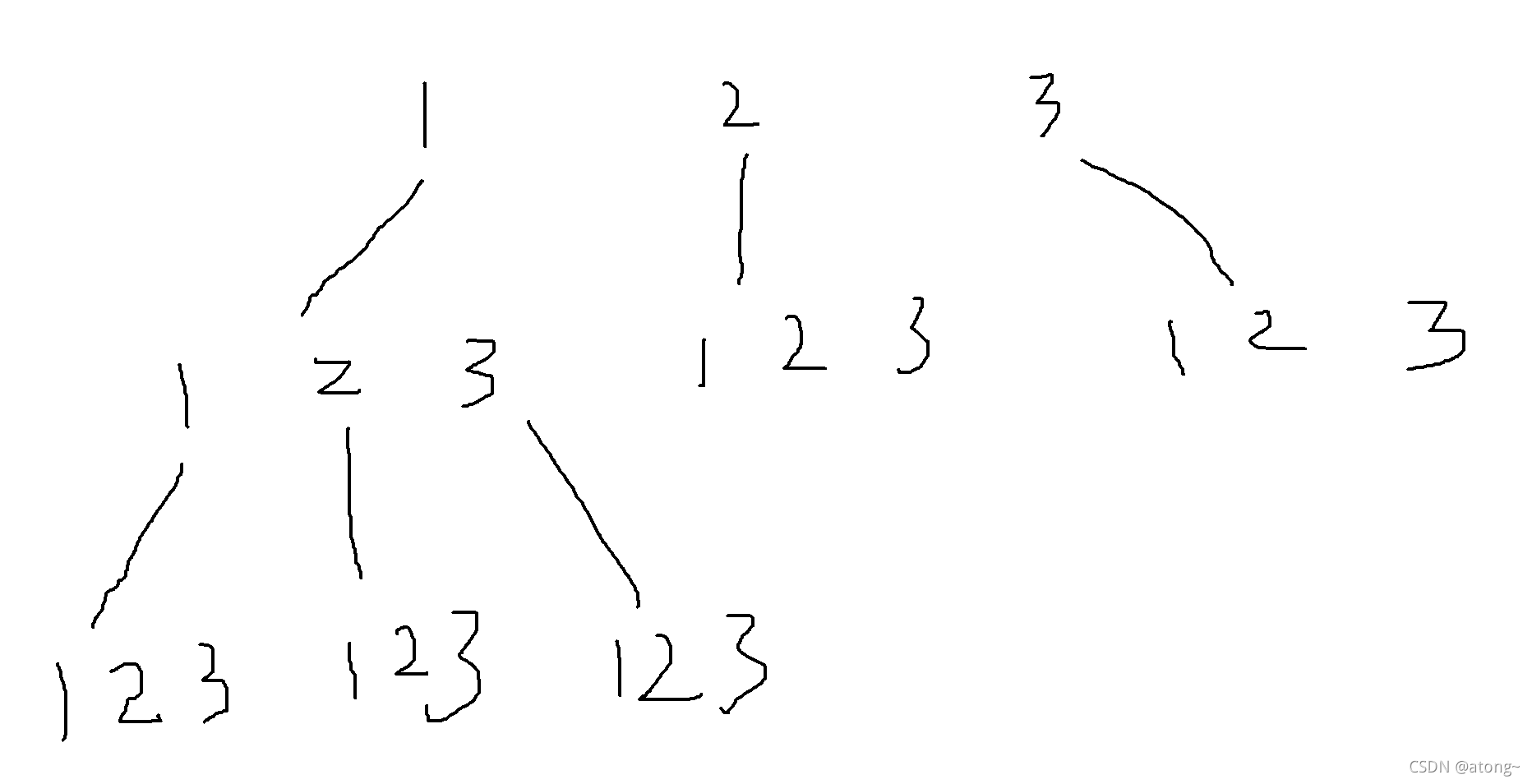
这个题打印部分很简答，难的地方是如何正确的分解这个数，分解完和为这个数的值就进行打印。如果单纯用循环遍历的话是很难完成这个工作的，所以就采用了回溯的方法，本质是递归暴力遍历，这个回溯有点像把一条线的东西变成面的那种树的形式遍历，横向有宽度，纵向有深度，以输入3为例，如下图：

但是如果只是这样遍历，我们会发现有很多的遍历是无用功，比如到了第三层，1之后的2和3是没有必要遍历的，因为和肯定是大于3的，那这个部分需要剪枝操作，减少时间复杂度，如下图：

出了上图这中情况其实还有别的地方需要剪枝操作的部分，也就是函数终止部分的设立，其实比较自然的想法是当纵向的和等于N时return，但是这样时间复杂度会增加，比如说下图情况，3下面的层是没必要遍历的。

由上面分析我们可以得出，在当前层的搜索需要限制条件，在一层往下一层搜索同样需要限制条件。

条件1：在回溯函数的for循环中范围为N-纵向存入数组中的数，这个很好理解，如题输入7，当纵向为7时，横向遍历就需要一次也就是只需要遍历1个1，再往后遍历肯定大于7.

条件2：return 的条件要设置为纵向的和大于N，如果设置等于N会出现上图情况，进行不必要的遍历。

下面是两个代码，并附上提交结果

代码1(终止条件不对超时)：

#include <iostream>
#include <vector>
#include <numeric>

using namespace std;

class Solution
{
private:
	vector<int> tmp;
	vector<vector<int>>result;
	
	void backtracking(int n,int startIndex)
	{
		if (accumulate(tmp.begin(), tmp.end(), 0) == n)
		{
			result.push_back(tmp);
			return;
		}

		for (int i = startIndex; i <= n-tmp.size(); i++)
		{
			tmp.push_back(i);
			backtracking(n, i);
			tmp.pop_back();
		}
	}
	void getnum()
	{
		cin >> n;
	}
public:
	int n = 0;
	int count = 0;
	void show()
	{
		getnum();
		backtracking(n, 1);
		for (vector<vector<int>>::iterator it = result.begin(); it != result.end(); it++)
		{
			cout << n << "=";
			for (vector<int>::iterator tit = it->begin(); tit != it->end(); tit++)
			{
				cout << *tit;
				if (tit < it->end() - 1)
				{
					cout << "+";
				}
			}	
	
			count++;
			if (count < 4 && it<result.end()-1)
			{
				cout << ";";
			}
			if (count == 4)
			{
				cout << endl;
				count = 0;
			}
		}
	}
};
int main()
{
	Solution s;
	s.show();
	return 0;
}

终止条件设立不好时运行时间

代码2（AC）:

#include <iostream>
#include <vector>
#include <numeric>

using namespace std;

class Solution
{
private:
	vector<int> tmp;
	//vector<vector<int>>result;
	int count = 0;
	void backtracking(int n, int startIndex)
	{
		if (accumulate(tmp.begin(), tmp.end(), 0) == n)
		{
			//result.push_back(tmp);

			cout << n << "=";
			for (vector<int>::iterator it = tmp.begin(); it != tmp.end(); it++)
			{
				cout << *it;
				if (it < tmp.end() - 1)
				{
					cout << "+";
				}
			}
			count++;
			if (count < 4 && tmp.size()>1)
			{
				cout << ";";
			}
			if (count % 4 == 0)
			{
				cout << endl;
				count = 0;
			}
		}

		if (accumulate(tmp.begin(), tmp.end(), 0) > n)
		{
			return;
		}
		for (int i = startIndex; i <= n - tmp.size(); i++)
		{
			tmp.push_back(i);
			backtracking(n, i);
			tmp.pop_back();
		}
	}


	void getnum()
	{
		cin >> n;
	}


public:
	int n = 0;

	void show()
	{
		getnum();
		backtracking(n, 1);
	}
};
int main()
{
	Solution s;
	s.show();
	return 0;
}

提交结果：