KZG批量验证方案--shPLONK

本文前序博客有
KZG承诺(1)–预备知识
KZG承诺(2)–方案构建流程
KZG承诺(3)–批量验证方案

SHPlonk–Efficient polynomial commitment schemes for multiple points and polynomials是2021年提出的批量KZG多项式承诺方案，针对多个多项式在多个评估点打开的情景下的方案进行优化。文中提出了两种优化的批量证明方案，第一个方案多个多项式的开放证明仅为一个元素，且每个多项式在不同的任意点子集上进行评估。第二个方案多项式的开放证明为两个个元素，但验证效率高于其他方案。

虽然SHPlonk的效率表现很优异，但是核心思想还是我们之前使用的两个基础工具——零点证明+随机线性化组合。先回顾一下前面的内容，我们再继续下面的学习。

第一个方案

进入正题，依旧采用多个多项式在多个点打开和验证的例子，在采用零点证明将验证等式转换为以下等式的形式，（注意：这里的推理过程在上一节中，这里就不重复叙述）
$$\begin{gathered} f(r)-g(r)=h(r)(r-z_1)(r-z_2) \\ {f}^{\prime }(r)-g^{\prime }(r)=h^{\prime }(r)(r-z_3)(r-z_4) \end{gathered}$$
在KZG的多对多的批量验证我们已经介绍了采用随机线性化组合合并验证等式，但遗憾的是，和证明相关的项无法进行合并，因此无法缩小证明的大小。此时，为了缩小证明大小（或者说合并证明项），可以将等式其写成以下形式。
$$\begin{gathered} \frac{f(r)-g(r)}{z(r)}=h(r) \\ \frac{f^{\prime }(r)-g^{\prime }(r)}{z^{\prime }(r)}=h^{\prime }(r) \end{gathered}$$
其中，将$(r-z_1)(r-z_2)$表示成多项式形式$z(r)=r^2-(z_1+z_2)r+z_1{z}_2$，$(r-z_3)(r-z_4)$表示成多项式$z^{\prime }(r)=r^2-(z_3+z_4)r+z_3{z}_4$。
此时，验证者选择一个随机数$\xi$进行随机线性化组合合并验证等式为
$$\frac{f(r)-g(r)}{z(r)}+\xi \frac{f^{\prime }(r)-g^{\prime }(r)}{z^{\prime }(r)}=h(r)+\xi h^{\prime }(r)$$
因为$r$是密文，依据原有的$srs=([1{]}_1,[x{]}_1,[x^2{]}_1,\cdots ,[x^n{]}_1,[1{]}_2,[x{]}_2)$是无法计算$[z(r{)}^{-1}{]}_2,[z^{\prime }(r{)}^{-1}{]}_2$，因为无法得到$[r^{-1}{]}_2,[r^{-2}{]}_2$。此时一个简单的方法是等式两边同时乘值$Z_T(r)=z(r)z^{\prime }(r)$，此时需要验证的多项式为
$$(f(r)-g(r))z^{\prime }(r)+\xi (f^{\prime }(r)-g^{\prime }(r))z(r)=(h(r)+\xi h^{\prime }(r))Z_T(r)$$
，则对应的验证等式为
$$e([f(r)-g(r){]}_1,[z^{\prime }(r){]}_2)\cdot e(\xi [f^{\prime }(r)-g^{\prime }(r){]}_2,[z(r){]}_2)=e([h(r)+\xi h^{\prime }(r){]}_1,[Z_T(r){]}_2)$$
，这是的评估证明为$[h(r)+\xi h^{\prime }(r){]}_1$，整体流程如图所示。

此时，根据以上例子，我们假设有$m$个多项式，分别在集合$S_1,S_2,...,S_m$上打开和验证，其中 m a x = m a x { ∣ S 1 ∣ , ∣ S 2 ∣ , . . . , ∣ S m ∣ } max=max{\{|S_1|,|S_2|,...,|S_m|\}} max=max{∣S1​∣,∣S2​∣,...,∣Sm​∣}，$T=S_1\bigcup ...\bigcup S_m$，这种情况下的证明开销与KZG的批量证明对比如表所示。

$m$个多项式在多个评估点	srs	证明验证开销	证明大小
批量验证	$n+2+max$	$(max+1)P+(3m-2)M$	$m$
SHPlonk1	$n+2+	T	$

从对比来看，SHPlonk第一个方案的证明大小仅需一个群元素，但验证开销和srs的开销都增加了。因此这种方案更适用于对通信开销要求较为严格的方案。

第二个方案

虽然第一种方案在证明大小上已经达到了最优，但增加了验证开销。众所周知，ZK-SNARK对验证效率要求高，因此，SHPlonk在第一个方案的基础上进行了优化，减少验证开销。

接着上节的内容，我们基于方案一考虑如何优化验证开销。我们依旧从熟悉的两种工具开始考虑如何优化验证开销。

首先，思考一下随机线性化组合可以优化等式 (36) 吗？很遗憾，随机线性组合只对多个验证等式合并有用，此时仅为一个验证等式，这并不适合此种方式优化。

然后，考虑一下零点证明好像可以在此处使用，我们进行一下尝试，首先将多项式的右侧移到左侧，可看作一个多项式$F(x)$在$r$点为零，即
$$(f(r)-g(r))z^{\prime }(r)+\xi (f^{\prime }(r)-g^{\prime }(r))z(r)-(h(r)+\xi h^{\prime }(r))Z_T(r)=0$$
。注意，这个等式不是只在$r$点为零，在任意点上均成立（原等式是随机选择一个点证明等式两边成立）。但因为$r$是密文，证明人无法计算此次零点证明的多项式$H(x)$。因此，验证者可以重新选择一个点$\theta$来确保等式两边成立，因此转换为证明$F(\theta )=0$，运用零点证明，再转换为证明存在多项式$H(x)$使得以下验证等式成立。
$$(f(x)-g(x))z^{\prime }(x)+\xi (f^{\prime }(x)-g^{\prime }(x))z(x)-(h(x)+\xi h^{\prime }(x))Z_T(x)=H(x)(x-\theta )$$
此时验证等式等同于
$$(f(x)-g(\theta ))z^{\prime }(\theta )+\xi (f^{\prime }(x)-g^{\prime }(\theta ))z(\theta )-(h(x)+\xi h^{\prime }(x))Z_T(\theta )=H(x)(x-\theta )$$
，这个转换如果大家有疑问可以看**补充知识点**，设左边等式为$L(x)$，此时，随机选取一个点$r$检查两边等式是否相等。则此时评估证明除了$[h(r)+\xi h^{\prime }(r){]}_1$，还需$[H(r){]}_1$，此时完成流程如下所示。

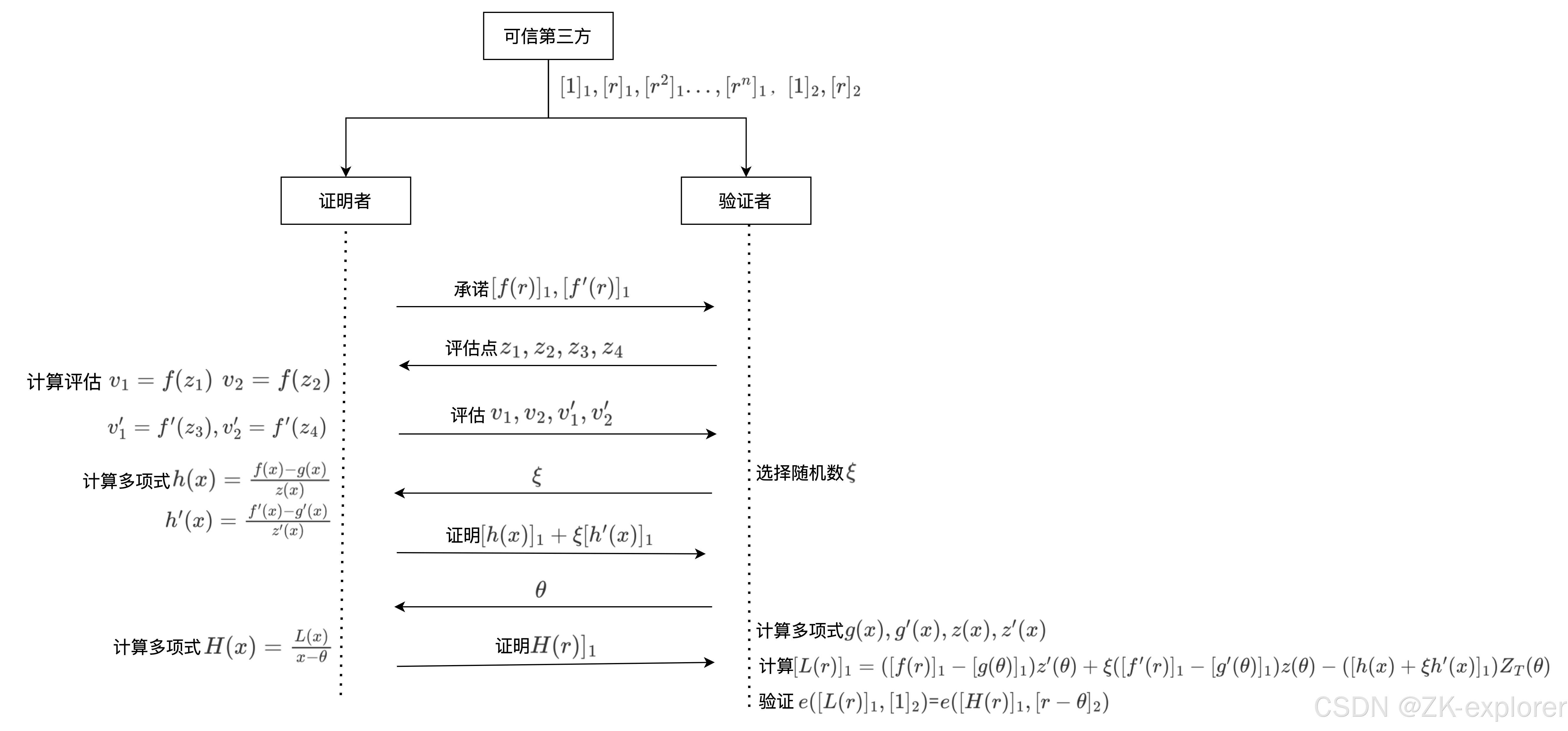
此时，根据以上例子，我们假设有$m$个多项式，分别在集合$S_1,S_2,...,S_m$上打开和验证，其中 m a x = m a x { ∣ S 1 ∣ , ∣ S 2 ∣ , . . . , ∣ S m ∣ } max=max{\{|S_1|,|S_2|,...,|S_m|\}} max=max{∣S1​∣,∣S2​∣,...,∣Sm​∣}，$T=S_1\bigcup ...\bigcup S_m$，这种情况下的证明开销与KZG的批量证明对比如表所示。

$m$个多项式在多个评估点	srs	证明验证开销	证明大小
批量验证	$n+2+max$	$(max+1)P+(3m-2)M$	$m$
SHPlonk1	$n+2+	T	$
SHPlonk2	$n+3$	$2P+(	S_1

可以看出SHPlonk的第二个方案验证开销非常小，特别是最耗时的双线性配对操作仅需2次，与多项式个数和评估点的个数无关，且证明大小也是常数级的，因此在大多情况下采用SHPlonk的第二个方案都是比较好的选择。

看到此处，恭喜你已经掌握了批量证明方案的构建和适用场景。注意本文的KZG协议都是交互式，但在实际运用中，例如在Plonk论文中，可运用Fait-Shamir启发式讲上述交互式方案转换成非交互式方案。

补充知识点

我们运用零点证明去证明$f(z)-g(z)=0$，常常我们去证明多项式$f(x)-g(x)$在点$z$为零。即证明存在$h(x)$使得等式$f(x)-g(x)=h(x)(x-z)$成立。其实我们还可以证明多项式$f(x)-g(z)$在点$z$为零。即证明存在$h(x)$使得等式$f(x)-g(z)=h(x)(x-z)$成立。当然，也可证明多项式$f(z)-g(x)$在点$z$为零。即证明存在$h(x)$使得等式$f(z)-g(x)=h(x)(x-z)$成立。