网络流最大流最小费用流

最新推荐文章于 2020-12-22 18:30:36 发布

是哆啦D梦

最新推荐文章于 2020-12-22 18:30:36 发布

阅读量1.3k

点赞数 1

文章标签：网络

本文链接：https://blog.youkuaiyun.com/weixin_43602607/article/details/110135388

版权

网络流学习

一.最大流
二.最小费用最大流
- 模板
- 最大费用最大流
三.二分图最大匹配训练
四.最小割训练
上下界最大流
- - 例题1：无源汇上下界可行流

一.最大流

模板题
题目描述： 给定一个网络图，及其源点和汇点，和点的连接关系，以及边的容量限制，求出其网络最大流。
问：什么是最大流？？？
答：源点无限制向外流水，但由于边的容量限制，只有一部分留到汇点，流入汇点的最大流量就是网络最大流）
算法：常见的算法有EK，dinic，isap。下面只学dinic+弧优化

dinic算法学习

基本思路：重复不断的从残余网络中寻找增广路来增广流量。

观察下图：
在这里插入图片描述
怎么找增广路？？？dfs大胆找就行，我们先不管正确性
假设找的增广路是1-2-3-4，该增广路为汇点贡献了1的流量。此时1-2,2-3,3-4这三条路的容量均达到的上限，不能再继续增广。但显然1不是最优答案，2才是。
为什么错了？？是因为我们没有给程序一个反悔的机会。
回溯的时候反悔？？那样程序的时间复杂度就升成指数级了
怎么反悔？？反向+flow，看下图
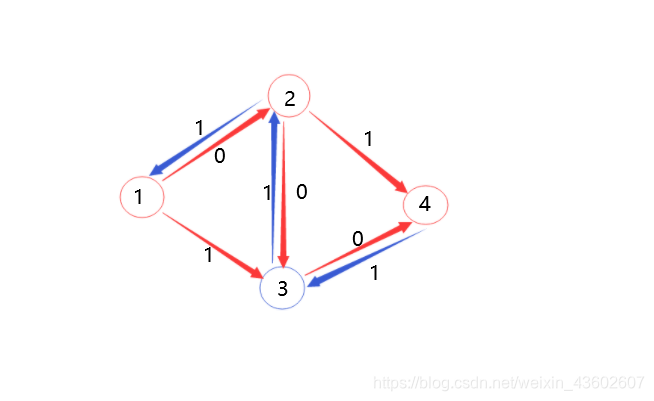
在这里插入图片描述
该图S到T再增广一条1-3-2-4为汇点再贡献1的流量。答案为2正确。

正确性：当我们第二次的增广路走3-2这条反向边的时候，就相当于把2-3这条正向边已经用了的流量给”退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流量。
这就是这个算法的精华部分，利用反向边，使程序有了一个后悔和改正的机会。

效率提升：为使跑残余网络时少走重复的路，每次用bfs为残余网络建立分层图。dfs求增广路的时候，我们只会从分层图中层次低的点走到层次高的点。总时间复杂度为O(n²m)。对于二分图，总时间复杂度为O(msqrt(n))，比匈牙利还快。

当前弧优化
对于每一个点，都记录上一次检查到哪一条边。因为我们每次增广一定是彻底增广（即这条已经被增广过的边已经发挥出了它全部的潜力，不可能再被增广了），下一次就不必再检查它，而直接看第一个未被检查的边。实现方法：用一个temp数组复制链式前向星的head数组（我这里是用vex），用到哪个temp[u]，就用temp[u]=i。

模板

#include<bits/stdc++.h>
using namespace std;
const int N=205;
const int M=50005;
const long long inf=1e15;
struct ppp {
	int u,v,next;
	long long f;
} e[M];
int vex[N],k=-1,dis[N];
int temp[N];
int S,T,n,m;
queue<int>q;

void init() {
	k=-1;
	for(int i=1; i<=T; i++)vex[i]=-1;
	//因为边的编号从0开始，所以点遍历的结束条件就不能是i==0了
	//所以我们给vex附上初始值-1，则i==-1为其结束条件
}
void add(int u,int v,long long f) {
	k++;
	e[k].u=u;
	e[k].v=v;
	e[k].f=f;
	e[k].next=vex[u];
	vex[u]=k;
}
int bfs() { //bfs将残余网络分层
	memset(dis,-1,sizeof(dis));
	q.push(S);
	for(int i=1; i<=T; i++)temp[i]=vex[i];
	dis[S]=0;
	while(!q.empty()) {
		int u=q.front();
		for(int i=vex[u]; i!=-1; i=e[i].next) {
			int v=e[i].v;
			if(dis[v]==-1&&e[i].f>0) {
				dis[v]=dis[u]+1;
				q.push(v);
			}
		}
		q.pop();
	}
	return dis[T]!=-1;//判断残余网络是否能连通到 T点
}
long long dfs(int u,long long exp) { //exp经过u点时当前流量
	if(u==T)return exp;//能留到汇点的流量即为增广流量
	long long flow=0; //定义flow为在u点所增广的流量总和
	for(int i=temp[u]; i!=-1; i=e[i].next) {
		temp[u]=i;
		int v=e[i].v;
		if(dis[v]==dis[u]+1&&e[i].f>0) {
			long long tmp=dfs(v,min(exp,e[i].f)) ;
			if(tmp==0)continue;
			exp-=tmp;//流量限制
			flow+=tmp;//从v点增广的流量加入u中
			e[i].f-=tmp;//这条路容量限制-=tmp
			e[i^1].f+=tmp;//允许反悔，反向边+=tmp
			if(exp==0)break;//流量不够，无法继续增广了
		}
	}
	if(flow==0)dis[u]=-1;
	//重要的优化条件！！！
	//我顺着残量网络，与终点不连通
	//上一层的点请别再信任我，别试着给我流量
	return flow;
}
void Dinic() {
	long long ans=0;
	while(bfs())ans+=dfs(S,inf);//每次都从残余网络中找增广路
	cout<<ans;
}
int main() {
	int u,v;
	long long f;
	cin>>n>>m>>S>>T;
	init();
	for(int i=1; i<=m; i++) {
		scanf("%d%d%lld",&u,&v,&f);
		add(u,v,f);//因为要用到反向边，所以建边的编号从0开始
		add(v,u,0);//因为后面要用到反向边加流量
	}
	Dinic();
	return 0;
}

无向图

直接正反两边都建一条 f 边就可以了。

for(int i=1; i<n; i++) {
	scanf("%d%d%lld",&u,&v,&f);
	add(u,v,f);
	add(v,u,f);
}

拆点

网络流的模板都是针对边的容量限制来写的最大流，而对于点的使用次数限制，我们可以通过拆点来写。

二.最小费用最大流

模板

模板题

题目描述： 给定一个网络图，及其源点和汇点，和点的连接关系，边的容量限制，以及每条边单位流量的花费，求出最大流时的最小花费。

方法： 将 dinic 求最大流时的 bfs 分层改为 spfa 即可，增广的时候只增广这条增广路。看注释

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+100;
const int M=2e5+100;
const long long inf=1e15;
struct ppp {
	int u,v,next;
	long long f,w;
} e[M];
long long vex[N],k=-1;
long long dis[N],vis[N];//spfa模板 
long long flow[N],pre[N],pos[N];//存储路径上的限制流，最短路径v的前一个结点u，u到v这条边的编号 
long long maxflow,mincost;//最大流，最小费用 
int temp[N];//当前弧优化 
int S,T,n,m;
queue<int>q;

void init() {
	k=-1;
	for(int i=1; i<=n; i++)vex[i]=-1;
}
void add(int u,int v,long long f,long long w) {
	k++;
	e[k].u=u;
	e[k].v=v;
	e[k].f=f;
	e[k].w=w;
	e[k].next=vex[u];
	vex[u]=k;
}
int spfa() { //spfa将残余网络分层
	memset(pre,-1,sizeof(pre));
	memset(vis,0,sizeof(vis));
	for(int i=1; i<=n; i++)temp[i]=vex[i];
	for(int i=1; i<=n; i++)dis[i]=inf;
	
	q.push(S);
	dis[S]=0;
	flow[S]=inf; 
	while(!q.empty()) {
		int u=q.front();
		vis[u]=0;
		for(int i=vex[u]; i!=-1; i=e[i].next) {
			int v=e[i].v;
			if(e[i].f>0&&dis[v]>dis[u]+e[i].w) {
				dis[v]=dis[u]+e[i].w;
				pre[v]=u;
				pos[v]=i;
				flow[v]=min(flow[u],e[i].f);//限制流的大小等于最短路径上的最小容量 
				if(vis[v]==0) {
					q.push(v);
					vis[v]=1;
				}
			}
		}
		q.pop();
	}
	return pre[T]!=-1;//判断残余网络是否能连通到 T点
}
void MCMF() {//沿着最短路增广
	int	v=T;
	while(v!=S){//从T到S倒着来 
		mincost+=flow[T]*e[pos[v]].w; 
	    e[pos[v]].f-=flow[T];
	    e[pos[v]^1].f+=flow[T];
		v=pre[v];
	}
	maxflow+=flow[T];
}
void Dinic() {
	while(spfa())MCMF();//每次都从残余网络中找增广路
	cout<<maxflow<<" "<<mincost;
}
int main() {
	int u,v;
	long long f,w;
	cin>>n>>m>>S>>T;
	init();
	for(int i=1; i<=m; i++) {
		scanf("%d%d%lld%lld",&u,&v,&f,&w);
		add(u,v,f,w);//因为要用到反向边，所以建边的编号从0开始
		add(v,u,0,-w);//因为后面要用到反向边加流量
	}
	Dinic();
	return 0;
}

最大费用最大流

只需将费用w取相反数，最后将最小费用mincost也取相反数就可以了。

三.二分图最大匹配训练

网络流求二分图最大匹配

套路

建模： 构建一个源点 S 和汇点 T ，源点向二分图的每个左部点连一条容量为（该点可使用次数）的边，左部点向右部点连一条容量为 1 的边（表示该匹配只发生一次），右部点向汇点连一条容量为（该点可使用次数）的边。跑最大流模板即可。
输出匹配方案： 如果左部点与连向右部点的边容量为 0 ，则表示发生了匹配。

Code

int main(){
	for(int u=1;u<=n;u++){
		for(int i=vex[u];i!=-1;i=e[i].next){
			if(e[i].f==0){
				cout<<u<<" "<<e[i].v<<endl;
			}
		}
	}
}

例题1：网络流求二分图最大匹配（左右部点单次匹配）

例题链接

题目描述： 有 n 个外籍飞行员和 m 个英国飞行员，每架飞机需要一个外籍飞行员和一个英国飞行员，但前提是他们合作融洽。每个外籍飞行员与若干个英国飞行员合作融洽，题目会给出所有的合作融洽关系。求最多能派出多少架飞机。
问题分析： 外籍飞行员与英国飞行员就相当于二分图的左右部点，直接建图跑最大流即可。

例题2：网络流求二分图最大匹配（右部点允许两次匹配）

例题链接

题目描述： 已知车上有 N 排座位，有 $N\times 2$ 个人参加省赛，每排座位只能坐两人，且每个人都有自己想坐的排数，问最多使多少人坐到自己想坐的位置。
建模： 人与作为就相当于二分图的左右部点。源点与所有人连接一条容量为1的边（因为每个人只能算一次），将每个人与自己想坐的排数建一条容量为1的边（保证最多发生一次匹配）。所有排数与汇点连接一条容量为 2 的边（因为每排最多坐两个人）。这样最大流就是所求的答案了。

例题3：网络流求二分图最大匹配（右部点允许多次匹配）

题目描述：给定n个男生，m个女生，并给出所有相互喜欢的关系，即 u 与 v 可以匹配。男生只能匹配一个女生，女生可以匹配最多 k 个男生。求最大匹配。
建模：男生与女生就相当于二分图的左右部点。源点向男生连一条容量为1的边（每个男生只能算一次），男生向女生连一条容量为1的边（保证最多发生一次匹配），女生向汇点连一条容量为 k 的边（每个女生可以算 k 次），跑最大流即可。

例题4：网络流求二分图最大匹配（左右部点均允许多次匹配）

例题链接

题目描述： 有 n 个单位，每个单位 ri 人。有 m 个餐桌，每个餐桌 ci 人。是否可以达到下面这个目标：来自同一个的单位的人不在同一张作为吃饭。如果可以，请输出座位方案（第 i 行有 ri 个数，表示每个人在哪个餐桌吃饭）；如果不可以，则输出 0
建模： 单位与餐桌就相当于二分图的左右部点。源点向每个单位连一条容量为 ri 的边（表示第 i 个单位有 ri 个人可用），每个单位向所有餐桌都连一条容量为 1 的边（表示每个人只能坐一个位置，且不会有两个人去了同一张餐桌），每个餐桌向汇点连一条容量为 ci 的边（表示这张桌子只能坐 ci 人），跑最大流即可。若最大流等于总人数，则可以达到目标，输出一下方案。

网络流矩阵建模求二分图最大匹配

套路

通常： 物品的影响范围为其所在行和所在列，求物品之间没有互相影响（影响范围覆盖到其他物品）的情况下物品最多放置的数量。
建模：
题目限制条件等价于： 同一行只能放置一个炸弹，同一列只能放置一个炸弹。第 i 行第 j 列放置了一个炸弹等价于第 i 行与第 j 列发生了一个匹配。
将所有的行和列都定义上一个编号。将行当成左部点，列当成右部点，让源点向行连一条容量为 1 的有向边，列向右部点连一条容量为 1 的有向边（表示每行每列只能放置一个炸弹）。如果该点有可能放置物品，就让其所在行向其所在列连容量为 1 的有向边（表示该匹配最多发生一次）。跑最大匹配后得到的就是物品放置的最大数量。

例题1：炸弹摆放

例题链接

题目描述： n 行 m 列。上面有空地：可放置炸弹；有软石头：不可放置炸弹，炸弹可穿透软石头；有硬石头：不可放置炸弹，不可穿透软石头。一个炸弹的范围为其所在行和所在列的全部。求最多可以放置多少个炸弹，使得炸弹之间不会互相到。 $n,m\in[1,50]$
问题分析： 将所有的连续可炸到范围行和列都编上号，作为二分图左右部点，出现可以放置炸弹的点时，让其所在行向其所在列连一条容量为 1 的有向边即可。

int main() {
	cin>>n>>m;
	for(int i=1; i<=n; i++)cin>>s[i]+1;
	
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
			if((s[i][j]=='*'||s[i][j]=='x')&&(s[i][j-1]=='#'||j==1))cnt++;
			if(s[i][j]=='*')x[i][j]=cnt;
		}
	}	
	for(int j=1; j<=m; j++) {
		for(int i=1; i<=n; i++) {
			if((s[i][j]=='*'||s[i][j]=='x')&&(s[i-1][j]=='#'||i==1))top++;
			if(s[i][j]=='*')y[i][j]=top;
		}
	}	
	init();
	for(int i=1;i<=cnt;i++)add(S,i,1),add(i,S,0);
	for(int i=1;i<=top;i++)add(cnt+i,T,1),add(T,cnt+i,0);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(s[i][j]=='*')add(x[i][j],y[i][j]+cnt,1),add(y[i][j]+cnt,x[i][j],0);
		}
	}
	Dinic();
}

二分图的构造

套路

有些图匹配看似是个有向图，实际上点集可以分为两类，而匹配只会发生在两类之间。

例题1：有关数学的二分图构造，最大费用流

例题链接

题目描述： n 个数 $a_i$ ，每个数分别有 $b_i$ 个，点权为 $c_i$ 。两个数可以发生匹配当且仅当 $a_i/a_j$ 的结果是个质数的时候， $a_i$ 可以与 $a_j$ 发生匹配，得到的价值为 $c_i\times c_j$ 。求价值总和不小于 0 的情况下，可以进行的最多匹配次数。 $n\in[1,200],a_i\in[1,1e9],b_i\in[1,1e5],c_i\in[-1e5,1e5]$ 。
问题分析： 每个数字 $a_i$ 都有一个质因子数量，按照质因子的奇偶性拆分成两个部分。 $a_i/a_j$ 的结果为质数，那么该匹配只会发生在奇偶性不同的两部分中。

四.最小割训练

最小割点与最小割边模板

前言

定义最小割（边）： 选择一个边集，使得去掉这些边之后 S 与 T 不连通。求这个最小边权和。
定义最小割点： 选择一个点集，使得去掉这些点之后，S 与 T 不连通。求这个最小点权和。
结论： 最大流等于最小割边。直接用 Dicnic 跑最大流即可。

求解最小割点方法：

将一个点 i 拆成 i 和 i+n ，然后按下图

i 和 i+n 之间连了一条等于点权值的边，由于原有边只起到连接作用，不应该限制流量，故与原有的其他点连了一条 inf 边。这样就将最小割点的问题转化为了最小割边问题

例题1：最小割点板子

例题链接

题目描述： 给定一个无向连通图，求最少删除多少个点，使得删除这些点之后，起点到终点不连通。
问题分析： 无向图记得连反向边，然后按照上面那个图建即可。注意起点和终点是不能被删除的，因此我们可以定义起点和终点拆成的两个点中间边权为 inf ，这样这条边就永远不会被删除了。然后跑最大流即可。

for(int i=1;i<=n;i++){
	if(i==S||i==T){
		add(i,i+n,inf);
		add(i+n,i,inf);
		continue;
	}
	add(i,i+n,1);
	add(i+n,i,1); 
}
for(int i=1; i<=m; i++) {
	scanf("%d%d",&u,&v);
	add(u+n,v,inf);//因为要用到反向边，所以建边的编号从0开始
	add(v,u+n,inf);
	add(v+n,u,inf);
	add(u,v+n,inf);//因为后面要用到反向边加流量
}

例题2：最小割边并求割边数

例题链接

题目描述： 一张无向连通图，起点为 1 和终点为 n ，有边权 $w_i$ 。求最小割边以及最小割边的边数。
问题分析： 前一个问题可以直接求最大流解决，但是求边数不好办。
get 新技能： 想要在求解最大流时，附带边数。可以考虑将边权 $(x)$ 暂时转化为 $(x t + 1)$ ，其中 $t > M$ ，（ $M$ 为最大边数），得到最大流 $a n s$ 。那么 $a n s / t$ 即为最小割边， $ans\%t$ 即为最小割边的边数

void Dinic() {
	long long ans=0;
	while(bfs())ans+=dfs(S,inf);//每次都从残余网络中找增广路
	cout<<ans/t<<" "<<ans%t;
}
int main() {
	int u,v;
	long long f;
	cin>>n>>m;
	init();
	for(int i=1;i<=m;i++){
		cin>>u>>v>>f;
		add(u,v,f*t+1);
		add(v,u,0);
	}
	Dinic();
}

最小割建模1

套路

模型： n 对个物品，每对物品的两个物品权值分别为 $a_i,b_i$ ，每对物品

上下界最大流

例题1：无源汇上下界可行流

题目描述： 给定一张 n 个点 m 条边的有向图，每条边有容量上界 $(u, v)$ 和容量下界 $r (u, v)$ 。求一种可行方案使得在所有点满足流量平衡条件的前提下， $l (u, v) < = f (u, v) < = r (u, v)$
问题分析： 不妨设每条边已经流了 $b (u, v)$ 的流量，表示初始流，同时我们在新图中加入 u 连向 v 的容量为 $r (u, v) - b (u, v)$ 的边

例题2：最大流建模

建模： 源点向byx的第 i 点连一条 lifei 边，表示可以使用第 i 个点 lifei次。诗乃酱的第 i 个点向汇点连一条 lifei 边，表示可以使用第 i 个点 lifei 次。每对人之间只能比一次，所以如果能赢，就建一条 1 边，表示他们之间可以比一次。由于YYY会为J加生命，所以每个J的生命都要加上YYY的个数。再让T与T+1建一条m边，表示最多进行m场，然后跑S到T+1的最大流就ok了

例题3：最小费用流求二分图最小权匹配

题目描述： 给定n个男生和n个女生，以及每对男女的 $a_{ij}$ 和 $b_{ij}$ ，求出一个n对男女的匹配方案，使得所选的 $\frac{\sum ai}{\sum bi}$ 最大。
建模： 将源点与每个男生连一条流量为1，费用为0的边；将每个女生向汇点连一条流量为1，费用为0的边；根据分数规划，让每个男生向每个女生连一条容量为1，费用为 $a_{ij}-b_{ij}\times mid$ 的边。二分跑费用流模板即可。
建模含义： 易知该图的最大流为n，最小费用流一定会跑出最大流为n时的最小费用，即组合这n对关系后的最小费用。

例题4：拆点求网络流

题目描述： 给定一个数组a，设maxlen为其最长不下降子序列的长度。1：求在不重复使用点的情况下，子序列长度为maxlen的序列数量。2：求不限制使用第1个元素和第n个元素的情况下，子序列长度为maxlen的序列数量。
建模： 由于有点的使用次数的限制，故拆点 i 变为 i 和 i+n ，并从 i 向 i+n 连一条容量为1的边，表示只能使用一次。若 j <i 且 a[j]<=a[i] 且f[j]+1=f[i]，则从 j 向 i 连一条容量为1的边。若 f[i] = 1，则从 S 向 i 连一条容量为1的边，若 f[i] = k ，则从 i+n 向T连一条容量为1的边。
建模含义： 由于每次S都会从 f[i]=1 的点开始，以 f[i] 递增流，经过 f[i]=k 的点到达T结束，才会得到一条流量为1的流量，则这条流必然经过了maxlen个点，并使用了maxlen个点。