参考:算法导论中文第三版 p148
乘法散列法的基本定义如下,(书上说的很清楚,大家认真看下就行)
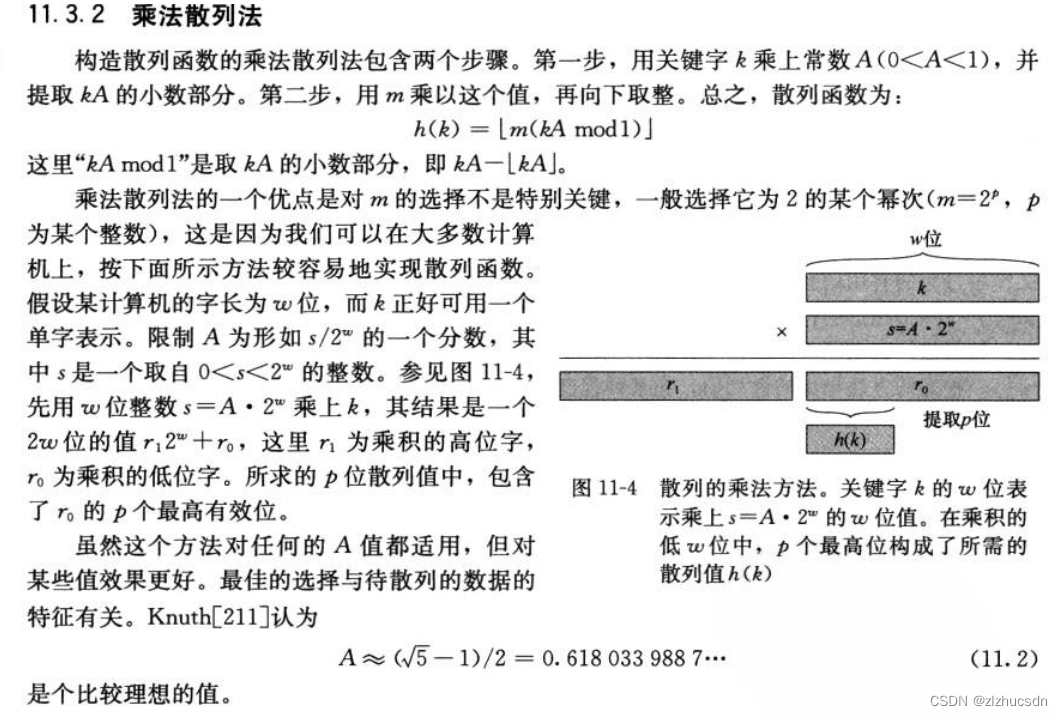
可能有同学疑问,当m = 2 ^ p 时,为什么 h(k) = r0 的二进制高p位?
下面,跟随一个例子,详细解析这个过程。

首先,常规乘法散列算法计算,h(k) = floor(m * ((k * A) mod 1)) 。

证明:当字长为w, m = 2^p, s = A * 2^w, 时,h(k) = floor[((s * k)& (2^w-1))>>(w-p)].也即使用了位运算,提高了计算速度。
证明过程如下,
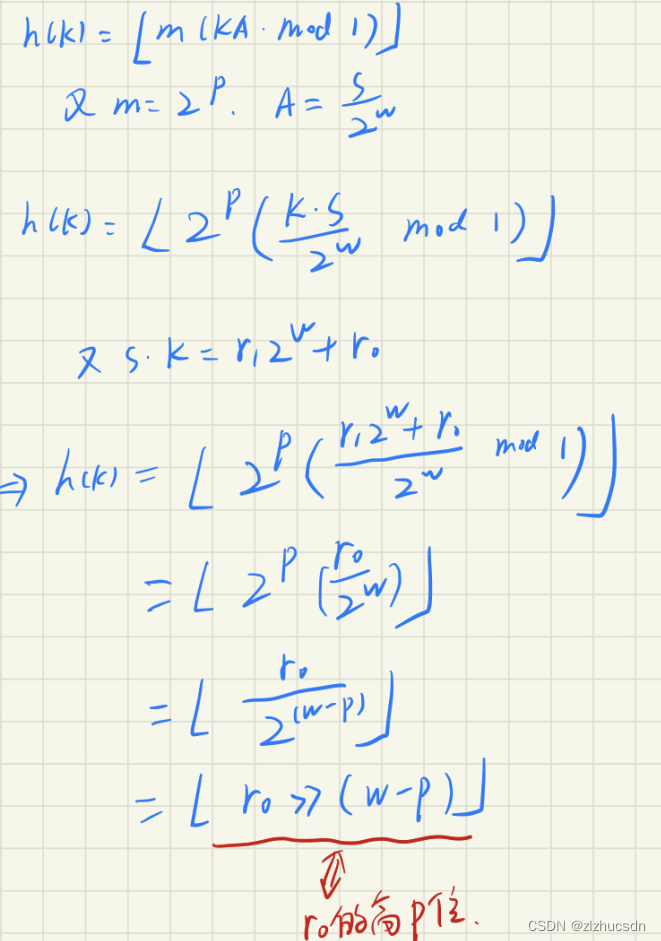
利用位运算,简化运算,提高运算速度。
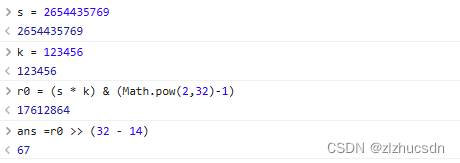
基于乘法散列法,也有斐波那契散列法,感兴趣的朋友,可以进一步了解一下。
本次写的博客有些匆忙,如果疏漏,欢迎同仁们批评改正!








 文章详细解释了乘法散列法中,当模数m为2的幂时,如何通过取k乘以A的高p位来计算h(k)的过程。通过位运算的使用,证明了这种方法能提高计算效率。此外,文中提及了与乘法散列法相关的斐波那契散列法,鼓励读者进一步探索。
文章详细解释了乘法散列法中,当模数m为2的幂时,如何通过取k乘以A的高p位来计算h(k)的过程。通过位运算的使用,证明了这种方法能提高计算效率。此外,文中提及了与乘法散列法相关的斐波那契散列法,鼓励读者进一步探索。
















 6
6

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








