线性回归与最小二乘法

欢迎关注”生信修炼手册”!

线性回归模型是使用最广泛的模型之一，也最经典的回归模型，如下所示

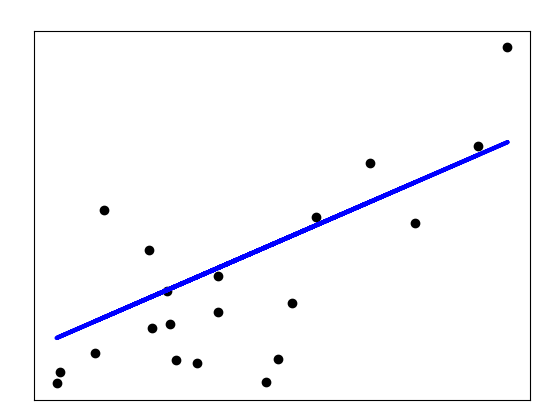
x轴表示自变量x的值，y轴表示因变量y的值，图中的蓝色线条就代表它们之间的回归模型，在该模型中，因为只有1个自变量x,所以称之为一元线性回归，公式如下

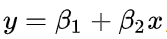
我们的目的是求解出具体的参数值，可以穿过这些点的直线可以有多条，如何选取呢？此时就需要引入一个评价标准。在最小二乘法中，这个评价标准就会误差平方和，定义如下

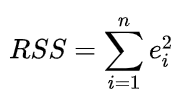
其中e表示通过回归方程计算出的拟合值与实际观测值的差，通过维基百科上的例子来看下实际的计算过程

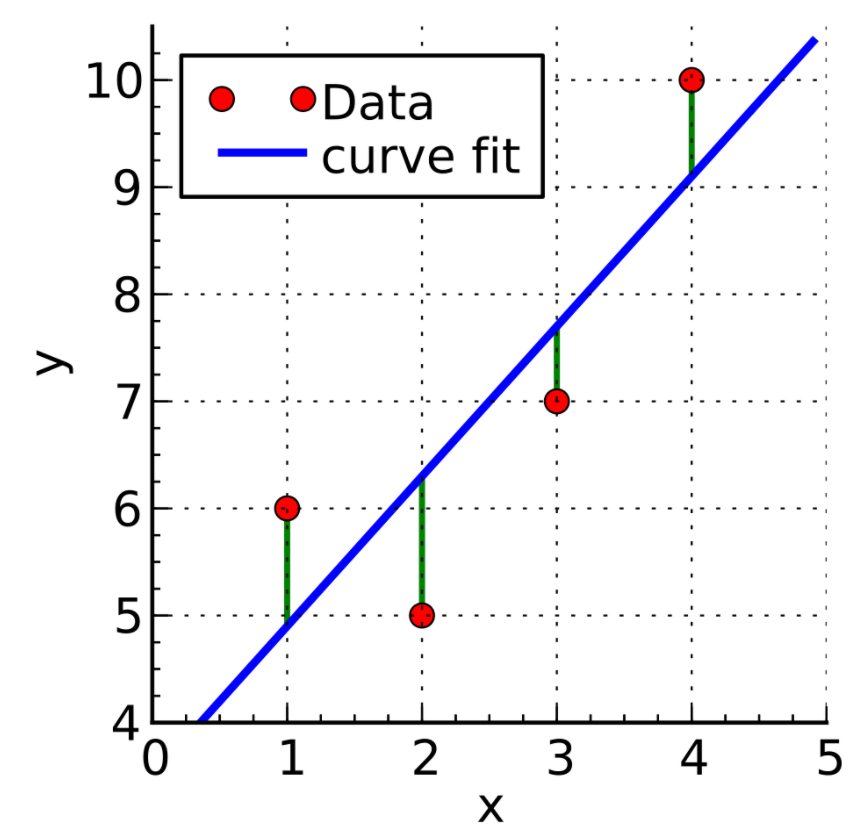
如上图所示，有4个红色的采样点，在每个点都可以得到(x, y)的观测值，将4个采样点的数据，带入回归方程，可以得到如下结果

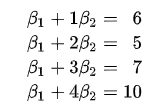
计算全部点的误差平方和，结果如下

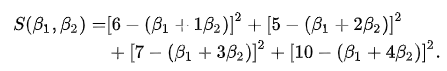
对于上述函数，包含了两个自变量，为了求解其最小值，可以借助偏导数来实现。通过偏导数和函数极值的关系可以知道，在函数的最小值处，偏导数肯定为0，所以可以推导出如下公式

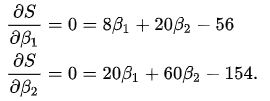
对于上述两个方程构成的方程组，简单利用消元法或者代数法就可以快速求出两个参数的值

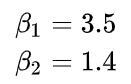
实际上，更加通过的方法是通过矩阵运算来求解，这种方法不仅适合一元线性回归，也适合多元线性回归，其本质是利用矩阵来求解以下方程组

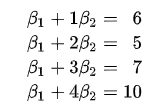
计算过程如下

>>> data = np.array([[1, 1], [1, 2], [1, 3], [1, 4]])
>>> data
array([[1, 1],
       [1, 2],
       [1, 3],
       [1, 4]])
>>> target = np.array([6,