目标跟踪PCRLB（后验克拉美罗下界）MATLAB仿真实现

UltraMan之神

已于 2024-11-29 23:52:39 修改

阅读量1.7k

点赞数 11

文章标签：目标跟踪 matlab 人工智能

于 2024-03-23 11:39:37 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_43475160/article/details/136963517

版权

PCRLB（后验克拉美罗下界）具有预测能力，能够通过递推的形式进行计算，能为下一时刻的目标状态估计误差提供下界，因此常被用作运动目标跟踪误差的评价准则。

用量测信息 $z_k^q$ 对目标状态向量 $x_k^q$ 进行估计时，其无偏估计量 $\hat{x}_{k|k}^{q}(z_k^q)$ 与目标状态向量间必须满足：

$J^{-1}(x_k^q)$ 表示 k 时刻目标 q 的 PCRLB，即关于 $x_k^q$ 的Fisher 信息矩阵(FIM, Fisher Information matrix)的逆。 FIM 可计算如下：

$P(z_k^q,x_k^q,)$ 表示状态向量与量测向量的联合 PDF：

k 时刻关于目标 q 的 FIM 的递推式可计算为：

这部分的参考文献如下：

本博客通过MATLAB对上述过程进行代码实现，通过UKF（无迹卡尔曼滤波）对目标状态进行跟踪滤波，并从仿真图中可以看到目标跟踪的位置RMSE与速度RMSE能够逐渐收敛到跟踪的PCRLB。仿真结果分别如下：

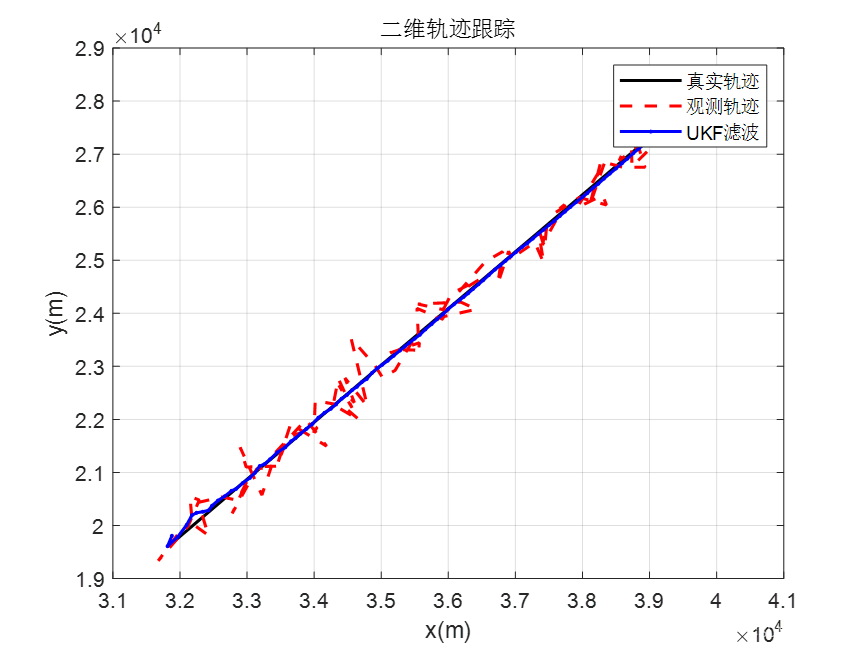
主要代码如下：

%% 参数定义
sV=zeros(n,N,MC,1); % 真实状态
eV=zeros(n,N,MC,chan); %状态估计
PV=zeros(n,n,N,MC,chan);
rV=zeros(3,N,MC,M); 
for i=1:MC

    x=[30000,80,20000,80]'; %初始状态变量
    P_0=diag([1e6,1e2,1e6,1e2]); %初始方差
    %滤波器初始化
    xk_UKF=x;   Pk_UKF=P_0;   % UKF单雷达滤波
    x0=mvnrnd(x,P_0); % 初始状态
    %x0=(x+normrnd(0,0.001)')';
    x=x0';
    for k=1:N
        %% 目标运动学模型，匀速运动CV模型
        w=sqrtm(Qk)*randn(4,1);%过程噪声
        x=Fk*x+Gk*w;
        sV(:,k,i,1)=x;
        %% radar measuremnt
        for m=1:M
            v=normrnd(v_mu,[sigma_r(m); sigma_b(m);sigma_d(m)]);
            % 两个雷达测量
            [r,b,d] = measurements3(x,xp(:,m)); %rm=距离，bm=角度 dm=多普勒速度
            rm=r+v(1);
            bm=b+v(2);
            dm=d+v(3);
            rV(:,k,i,m)=[rm,bm,dm]';  
        end
        % UKF
        [xk_UKF,Pk_UKF] = fun_3UKF(xk_UKF,Pk_UKF,Fk,Gk,rV(:,k,i,1),Qk,sigma_r(1),sigma_b(1),sigma_d(1),xp(:,1));
        PV(:,:,k,i,1)=Pk_UKF;%滤波方差
        eV(:,k,i,1)=xk_UKF;%滤波估计值， 1表示滤波结果
        % PCRLB
        [d11,d12,d22] = fun_pcrlbfusion(x,Fk,Gk,Qk,sigma_r,sigma_b,sigma_d,xp);
        d11_pcrlb(:,:,k,i)=d11;
        d12_pcrlb(:,:,k,i)=d12;
        d22_pcrlb(:,:,k,i)=d22;
    end
end

%雅可比矩阵
 Hk= [H11  0  H12  0 ;
      H21  0  H22  0 ;
      H31 H34 H32 H35 ];

%Fisher信息矩阵分量
-----------------此处省略-------------------

如有代码问题，请加V（UltraNextYJ）交流。