推荐系统XDeepFM模型--DeepFM和DCN升级版

目标：

学习模型xDeepFM模型,包含我个人的一些理解。深入理解模型。结合卷积神经网络CNN理解模型原理。昨晚想了一晚上才想通，都失眠了。
微软亚洲研究院2018年提出xDeepFM模型，可以理解为对DeepFM和DCN升级版。

• 相对于DeepFM，升级为自动构建高阶交叉特征
• 相对于DCN，从bit级别的交叉升级vector级别的交叉特征。

缺点：

• 计算量（时间复杂度）比前两者高。

---

引言：

xDeepFM模型，论文地址为：https://arxiv.org/abs/1803.05170

预测性系统，特征工程至关重要。特征工程中，挖掘交叉特征是至关重要的。交叉特征指的是两个或多个原始特征之间的交叉组合。例如，在新闻推荐场景中，一个三阶交叉特征为AND(user_organization=msra,item_category=deeplearning,time=monday_morning),它表示当前用户的工作单位为微软亚洲研究院，当前文章的类别是与深度学习相关的，并且推送时间是周一上午。

传统的推荐系统中，挖掘交叉特征主要依靠人工提取，这种做法主要有以下三种缺点：

• 1）重要的特征都是与应用场景息息相关的，针对每一种应用场景，工程师们都需要首先花费大量时间和精力深入了解数据的规律之后才能设计、提取出高效的高阶交叉特征，因此人力成本高昂；
• 2）原始数据中往往包含大量稀疏的特征，例如用户和物品的ID，交叉特征的维度空间是原始特征维度的乘积，因此很容易带来维度灾难的问题；–embeding技术不可少。
  3）人工提取的交叉特征无法泛化到未曾在训练样本中出现过的模式中。–不自动化。

因此自动学习特征间的交互关系是十分有意义的。目前大部分相关的研究工作是基于因子分解机的框架，利用多层全连接神经网络去自动学习特征间的高阶交互关系，例如FNN、PNN和DeepFM等。其缺点是模型学习出的是隐式的交互特征，其形式是未知的、不可控的；同时它们的特征交互是发生在元素级（bit-wise）而不是特征向量之间（vector-wise），这一点违背了因子分解机的初衷。
来自Google的团队在KDD 2017 AdKDD&TargetAD研讨会上提出了DCN模型，旨在显式（explicitly）地学习高阶特征交互，其优点是模型非常轻巧高效，但缺点是最终模型的表现形式是一种很特殊的向量扩张，同时特征交互依旧是发生在元素级（bit-wise）上。
我们用下图来回顾一下DCN的实现：

元素级（bit-wise）和特征向量（vector-wise）的意思

• bit-wise VS vector-wise
  假设隐向量的维度为3维，如果两个特征(对应的向量分别为$X1=[a1,b1,c1]$和$X2=[a2,b2,c2]$的话）在进行交互时:
  • bit-wise 的交互，比如DCN，基本上就是把$X1，X2$直接展平，拼接层一个一维的更长的向量，具体就是$[a1,b1,c1,a2,b2,c2]$,然后再进行特征的高阶交互时，也是基于$[a1,b1,c1,a2,b2,c2]$这个长向量进行的。所以叫基于位的高阶交互。
  • vector-wises是以向量为单位进行的交互，比如DeepFm就是人为的把$X1，X2$进行点积，产生如下的效果$[X{1}^T,X{2}^T]=[[a1,b1,c1],[a2,b2,c2]]$
    , 如果特征交互形式类似于 $f(w_1\ast a_1\ast a_2,w_2\ast b_1\ast b_2,w_3\ast c_1\ast c_2)$这样的效果，那么我们认为特征交互是发生在特征向量级（vector-wise）。

explicitly VS implicitly

• 显式的特征交互和隐式的特征交互。以两个特征为例$x_i$和$x_j$，在经过一系列变换后，我们可以表示成$w_{i,j}\ast (x_i\ast x_j)$的形式，就可以认为是显式特征交互，否则的话，是隐式的特征交互。

微软亚洲研究院社会计算组2018年提出了一种极深因子分解机模型（xDeepFM），不仅能同时以显式和隐式的方式自动学习高阶的特征交互，使特征交互发生在向量级，还兼具记忆与泛化的学习能力。是对Wide&Deep模型的升级。

xDeepFM模型介绍：

Compressed Interaction Network（CIN）

为了实现自动学习显式的高阶特征交互，同时使得交互发生在向量（vector）级上，文中首先提出了一种新的名为压缩交互网络（Compressed Interaction Network，简称CIN）的神经模型。在CIN中，隐向量是一个单元对象，因此我们将输入的原特征和神经网络中的隐层都分别组织成一个矩阵，记为$X_0$ 和 $X_k$ 。CIN中每一层的神经元都是根据前一层的隐层以及原特征向量推算而来，其计算公式如下：

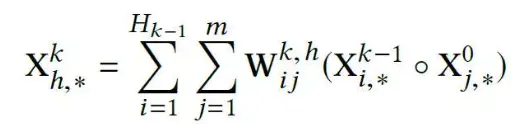
其中点乘的部分计算如下：

怎么理解这个公式，特别是$X_0$的作用是啥？这里的$X_0$再乘以$w_{Hi}$得到的$w_{Hi}\ast X_0$可以看做是一个$D\ast 1$维的卷积核，类比CNN模型中，我们一般采用2X2的卷积核，分别对图片进行扫描，这里也可以类似的理解。
看下卷积升级网络的操作：

类比：

这里详细详细展示了，用$w_{Hi}\ast X_0$当卷积核，产生最后的高阶向量。其中，$X_0$的每一列和$X_{k-1}$的每一列相乘，都采用了不同的权重$w_{Hi，m}$，所以权重向量还是比较大的，这个可以考虑类似于CNN卷积神经网络的共享权重，进行简化好，后续在探究。
作者原文中画的图太难看懂了，这里就不贴了，还是这个哥们帮忙理解的。

CIN的宏观框架可以总结为下图：

可以看出，它的特点是:

• 最终学习出的特征交互的阶数是由网络的层数决定的。因为每一层都是和$X_0$做卷积，所以每增加一层，就相当于$X_0$的阶数增加1。
• 每一层隐层都通过一个池化操作连接到输出层，从而保证了输出单元可以见到不同阶数的特征交互模式。
• 同时不难看出，CIN的结构与循环神经网络RNN是很类似的，即每一层的状态是由前一层隐层的值与一个额外的输入数据计算所得。不同的是，CIN中不同层的参数是不一样的，而在RNN中是相同的；RNN中每次额外的输入数据是不一样的，而CIN中额外的输入数据是固定的，始终是$X_0$。----RNN也能帮忙理解。

可以看到，**CIN是通过（vector-wise）**来学习特征之间的交互的，还有一个问题，就是它为什么是显式的进行学习？我们先从$X_1$ 来开始看，$X_1$ 的第$h$个神经元向量$x_h^1$可以表示成 ：

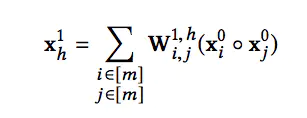
$X_1$ 可以看成是$X_0$自己跟自己做卷积。然后把$m$个向量的乘积全部相加。
进一步，$X_2$ 的第$h$个神经元向量可以表示成：

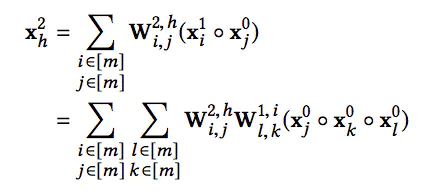
最后，第k层的第h个神经元向量可以表示成：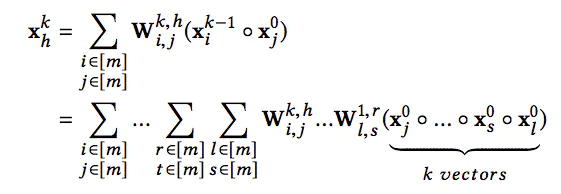
因此，我们能够通过上面的式子对特征交互的形式进行一个很好的表示，它是显式的学习特征交叉。即对每个特征都进行了高阶的相互组合再乘积。

xDeepFM

将CIN与线性回归单元、全连接神经网络单元组合在一起，得到最终的模型并命名为极深因子分解机xDeepFM，其结构如下图：

• 集成的CIN和DNN两个模块能够帮助模型同时以显式和隐式的方式学习高阶的特征交互
• 集成的线性模块LR和深度神经模块DN也让模型兼具记忆与泛化的学习能力。

值得一提的是，为了提高模型的通用性，xDeepFM中不同的模块共享相同的输入数据，这点在DCN模型中已经有过讨论。至少Wide变种模型和Deep模型输入相同，可以提升模型的学习速度。
而在具体的应用场景下，其他模块可以接入各自不同的输入数据，例如，线性模块中依旧可以接入很多根据先验知识提取的交叉特征来提高记忆能力，而在CIN或者DNN中，为了减少模型的计算复杂度，可以只导入一部分非稀疏的数值特征。

---

复杂度分析

假设CIN和DNN每层神经元/向量个数都为$H$ ，网络深度为$T$。那么CIN的参数空间复杂度为$O(mT{H}^2)$，普通的DNN为 $O(mDH+T{H}^2)$ ，CIN的空间复杂度与输入维度$D$无关，此外，如果有必要，CIN还可以对权重矩阵$W$进行 $L$ 阶的矩阵分解，从而能降低空间复杂度。

CIN的时间复杂度就不容乐观了，按照上面介绍的计算方式为 $O(m{H}^{2}DT)$ ，而DNN为 $O(mDH+T{H}^2)$ ，时间复杂度会是CIN的一个主要痛点。

Experiment

数据集原文

• 公开数据集 Criteo 与 微软数据集 BingNews
• DianPing 从大众点评网整理的相关数据，收集6个月的user check-in 餐厅poi的记录，从check-in餐厅周围3km内，按照poi受欢迎度抽取餐厅poi作为负例。根据user属性、poi属性，以及user之前3家check-in的poi，预测用户check-in一家给定poi的概率。
  

产出：

充分理解XDeepFM模型的原理，他的近亲是：DeepFM和DCN升级版
升级：
1、 思想上，采用了DCN（Deep&Cross）模型的特征自动交叉的，得到高阶特征。
2、特征交叉方式采用了DeepFM中FM的处理方式，不再是DCN中以位为单位，进行交叉，而是以向量为单位进行交叉。
3、 模型最后还添加了一个线性模型。

Conclusion

• 1. xDeepFM将基于Field的vector-wise思想引入Cross，并且保留了Cross的优势，模型结构也很elegant，实验效果也提升明显。如果说DeepFM只是“Deep & FM”，那么xDeepFm就真正做到了”Deep” Factorization Machine。
• 2. xDeepFM的时间复杂度会是其工业落地的一个主要性能瓶颈，需要重点优化

参考资料：

https://www.jianshu.com/p/b4128bc79df0
https://zhuanlan.zhihu.com/p/57162373