#2674. 「NOI2012」美食节

最新推荐文章于 2021-02-05 22:22:51 发布

Joker & Liar

最新推荐文章于 2021-02-05 22:22:51 发布

阅读量301

点赞数

CC 4.0 BY-SA版权

分类专栏：网络流文章标签：费用流

本文链接：https://blog.youkuaiyun.com/weixin_43209425/article/details/105369113

网络流专栏收录该内容

5 篇文章

订阅专栏

本文探讨了在解决大规模网络流问题时，如何通过动态添加边来优化最大流最小费用算法，以降低内存消耗和提高运行效率。文章详细介绍了算法的具体实现过程，包括SPFA最短路径算法的应用和关键代码解析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

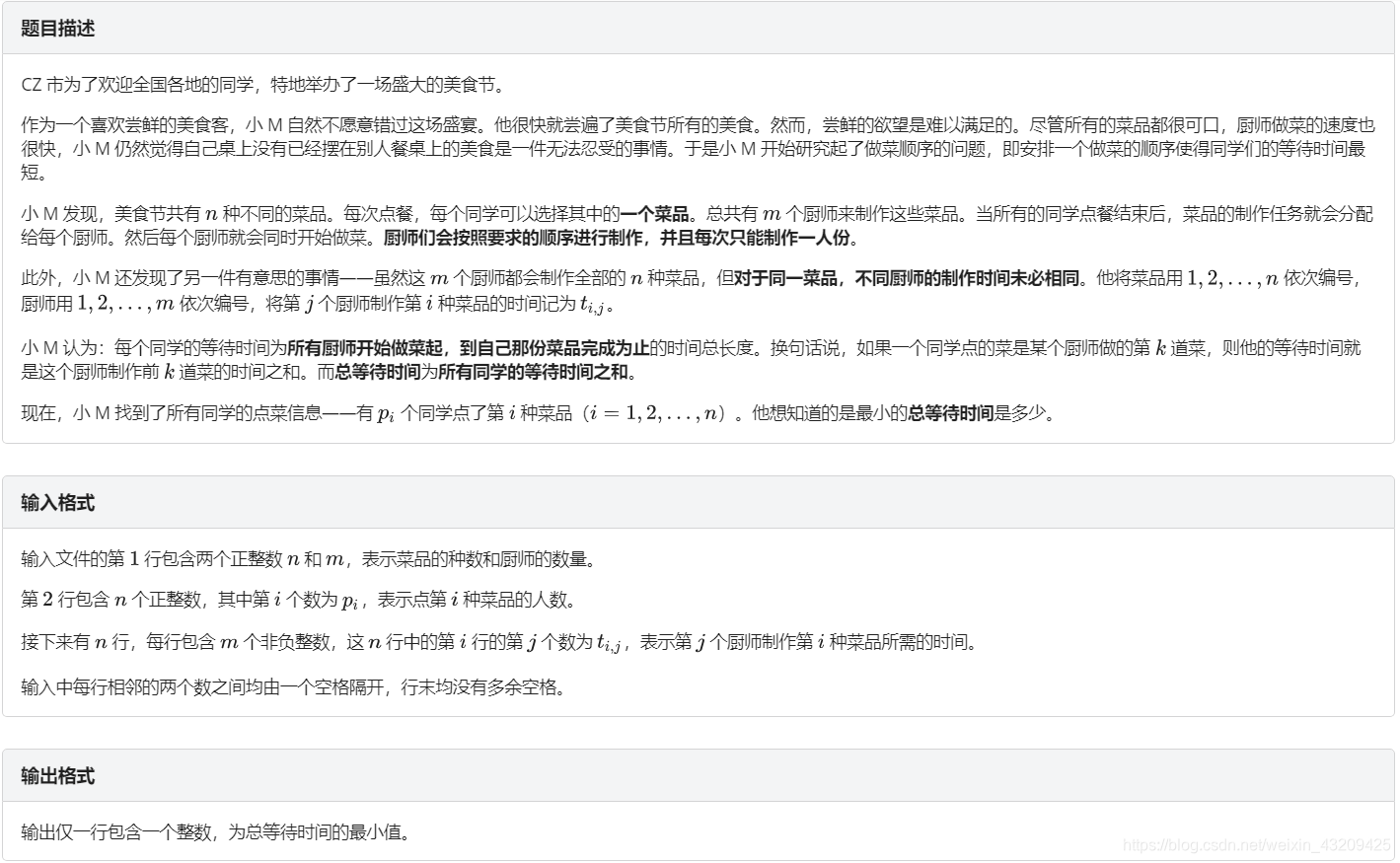
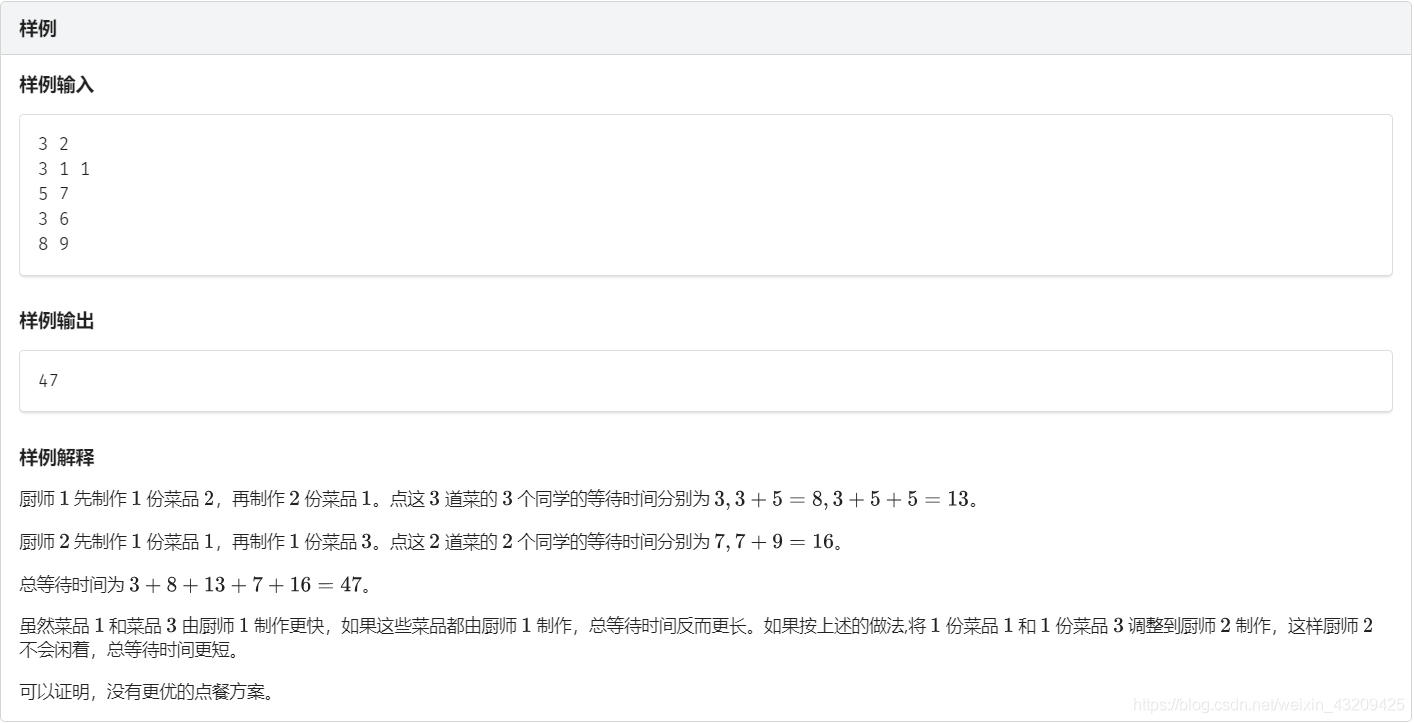
在这里插入图片描述

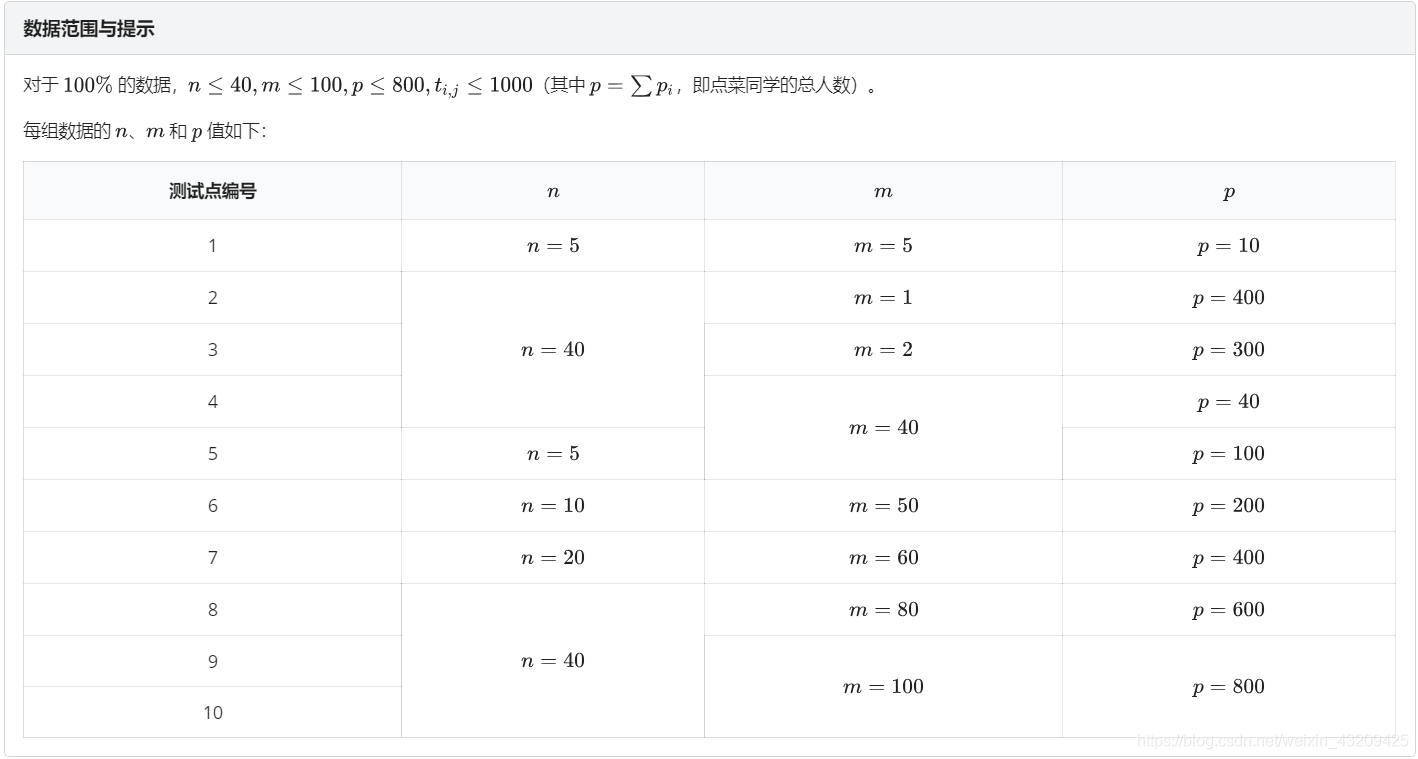
分析：

这题和 P2053 [SCOI2007]修车想法一样，把每个厨师拆成 p 个点按要求连边求最大流最小费用，但是拆点后最大有80000多个点，边都存不下(而且很多边完全用不到)，存下了直接求也肯定 T ，需要优化。
我们知道每次增广只求出一条增广路，那么就可以每次根据求出的增广路去添加相关的边。

代码：

#include<bits/stdc++.h>

#define rg register
#define I inline
using namespace std;

I int rd(){
    int x=0,f=0; char c=getchar();
    while(c<'0'||c>'9'){f|=c=='-';c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-48);c=getchar();}
    return f?-x:x;
}

const int N = 8E4+100;
const int M = 8E5+100;
const int INF = 1E9+1;

int lnk[N],ter[M],nxt[M],cap[M],cost[M],tot=1;
int n,m,dis[N],fa[M],id[M],flow[M];
bool vis[N];
int t[201][201],p[50],sum;

I void add(int u,int v,int w,int c){
    ter[++tot] = v,
      nxt[tot] = lnk[u],
      cap[tot] = w, 
     cost[tot] = c,
	    lnk[u] = tot;
}
I void addedge(int u,int v,int w,int c){   
    add(u,v,w, c), 
    add(v,u,0,-c);
}

int q[M],ANS,RET,S,T;

I bool spfa(){
	for(rg int i=0;i<=T;i++) dis[i]=INF,vis[i]=0;
   
    int l=0,r=0;q[0]=S;
    dis[S]=0,vis[S]=1,fa[S]=0,flow[S]=INF;
    while(l<=r)
	{
        int u=q[l++]; vis[u]=0;
        for (rg int i=lnk[u];i;i=nxt[i]){
            int v=ter[i];
            if(cap[i]>0&&dis[v]>dis[u]+cost[i])
			{
				fa[v]=u;
				id[v]=i;
				flow[v]=min(cap[i],flow[u]);
                dis[v]=dis[u]+cost[i];
                if(!vis[v]) q[++r]=v,vis[v]=1;
			}
        }
    }
    return dis[T]!=INF;
}

I void mcmf(){
    while(spfa())
	{
        int k = T;
        while(k!=S)
        {
        	cap[id[k]]  -= flow[T];
        	cap[id[k]^1]+= flow[T];
        	k=fa[k];
		}
        ANS+=flow[T];
        RET+=flow[T]*dis[T];
        int x=fa[T];
        addedge(x+1,T,1,0);
        for(rg int i=1;i<=n;i++){
        	addedge(i+sum*m,x+1,1,t[i][x/sum+1]*(x%sum+1));
        }
    
	}
}

int main() 
{
    n=rd(),m=rd(); 
    for(rg int i=1;i<=n;i++) p[i]=rd(),sum+=p[i];
    
	S=0,T=n+m*sum+1;
	for(rg int i=1;i<=n;i++)
	{
		addedge(S,sum*m+i,p[i],0);
	    for(rg int j=1;j<=m;j++)
	    {
	    	t[i][j]=rd();
	    	addedge(sum*m+i,sum*(j-1)+1,1,t[i][j]);
		}
	}  
	for(rg int i=1;i<=m;i++) addedge((i-1)*sum+1,T,1,0); 
	mcmf();
    printf("%d",RET);
    return 0;
}