概述
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
概率密度函数
若随机变量X服从一个数学期望为μ,标准差为σ的高斯分布,记为:
X
∼
N
(
μ
,
σ
2
)
X \sim N(\mu,\sigma^2)
X∼N(μ,σ2)
则其概率密度函数为:
f
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
2
σ
2
f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
f(x)=σ2π1e−2σ2(x−μ)2
高斯分布的期望值
μ
\mu
μ决定了其位置,标准差
σ
\sigma
σ决定了分布的概率。
(e是一个无理数,即无限不循环小数,e≈2.71828……)当x=μ时,函数达到峰值。
整个函数在x=
μ
\mu
μ左右两侧是对称的,x在
μ
−
σ
\mu-\sigma
μ−σ和
μ
+
σ
\mu+\sigma
μ+σ之间的样本数量占整个样本数量的68.2%,x在
μ
−
2
σ
\mu-2\sigma
μ−2σ和
μ
+
2
σ
\mu+2\sigma
μ+2σ之间的样本数量占整个样本数量的95.4%,x在
μ
−
3
σ
\mu-3\sigma
μ−3σ和
μ
+
3
σ
\mu+3\sigma
μ+3σ之间的样本数量占整个样本数量的99.6%。
μ
\mu
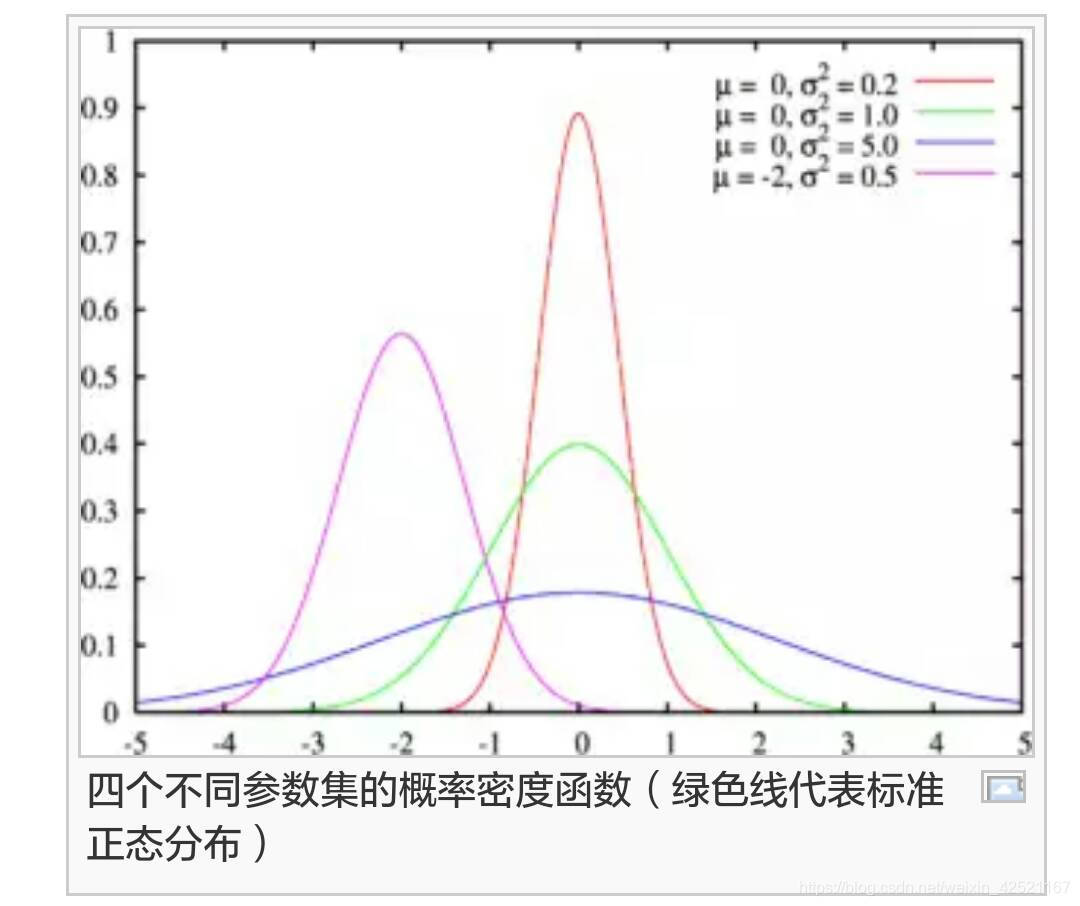
μ较大,则整个函数图像的中轴向右挪动比较多。
μ
\mu
μ较小,则整个函数图像的中轴向左挪动比较多。
σ
\sigma
σ较大,则整个曲线绵延比较长,整个坡度显得平缓。
σ
\sigma
σ较小,整个曲线窄而立陡。
因其曲线呈钟型,所以人们又称之为钟型曲线。
我们通常所说的标准正太分布是
μ
=
0
\mu=0
μ=0,
σ
2
=
1
\sigma^2=1
σ2=1的正太分布。
 深入理解高斯分布与正态分布
深入理解高斯分布与正态分布





 这篇博客详细介绍了高斯分布,又称正态分布,它在统计学中具有重要地位。文章涵盖概率密度函数,指出期望值μ决定分布的位置,标准差σ影响分布的形状。对于标准正态分布,其μ=0,σ=1,形成的钟型曲线是统计学中的基本概念。
这篇博客详细介绍了高斯分布,又称正态分布,它在统计学中具有重要地位。文章涵盖概率密度函数,指出期望值μ决定分布的位置,标准差σ影响分布的形状。对于标准正态分布,其μ=0,σ=1,形成的钟型曲线是统计学中的基本概念。
















 3443
3443

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








