二阶齐次线性微分方程的通解公式_一阶非齐次线性微分方程求解及应用举例

本文主要内容：介绍一阶非齐次线性微分方程的通解的应用、特解求解举例，以及二阶微分方程可用该通解求解的情形。

一、方程通解公式

一阶非齐次线性微分方程的解析式为：y'+p(x)=q(x),

则其通解表达式如下：y=e^[-∫p(x)]dx{∫q(x)*e^[∫p(x)dx]dx+c}.

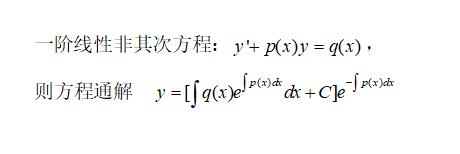
二、通解公式的实际应用

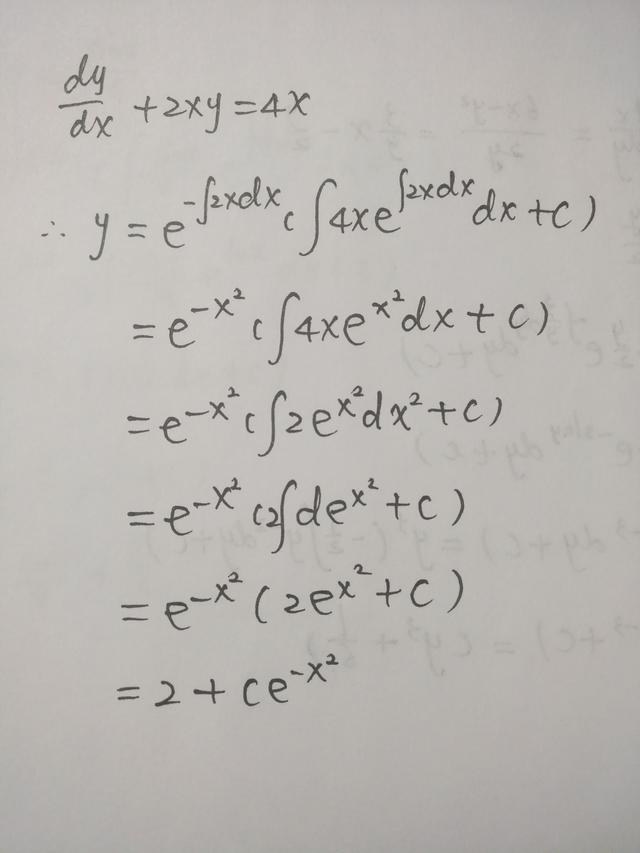
本例中，p(x)=2x，q(x)=4x.

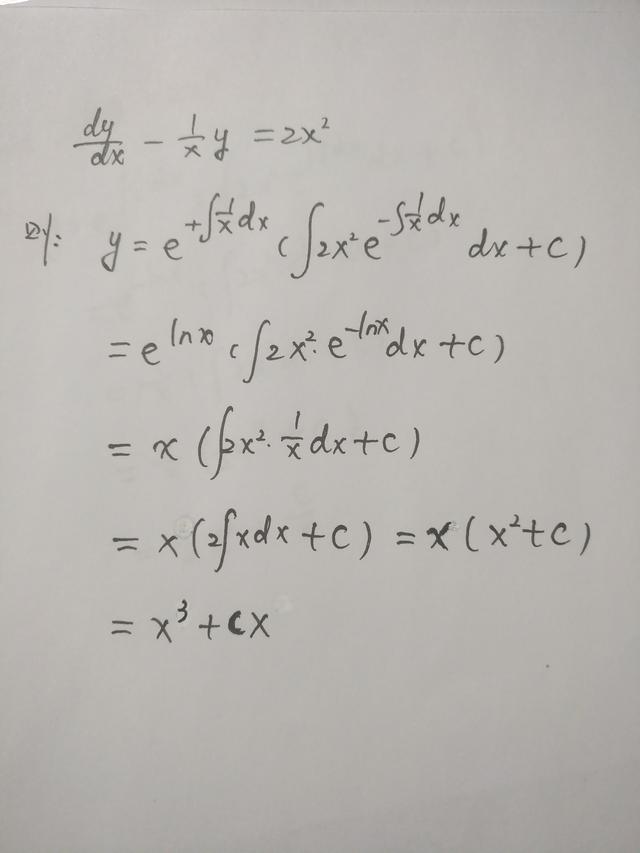
本例中，p(x)=-1/x，q(x)=2x^2.

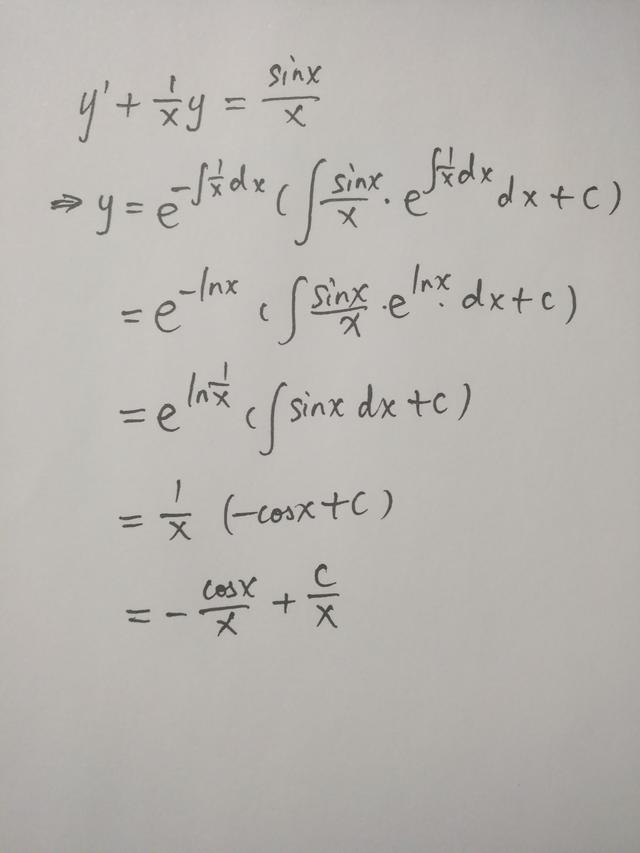
本例中，p(x)=1/x，q(x)=sinx/x.

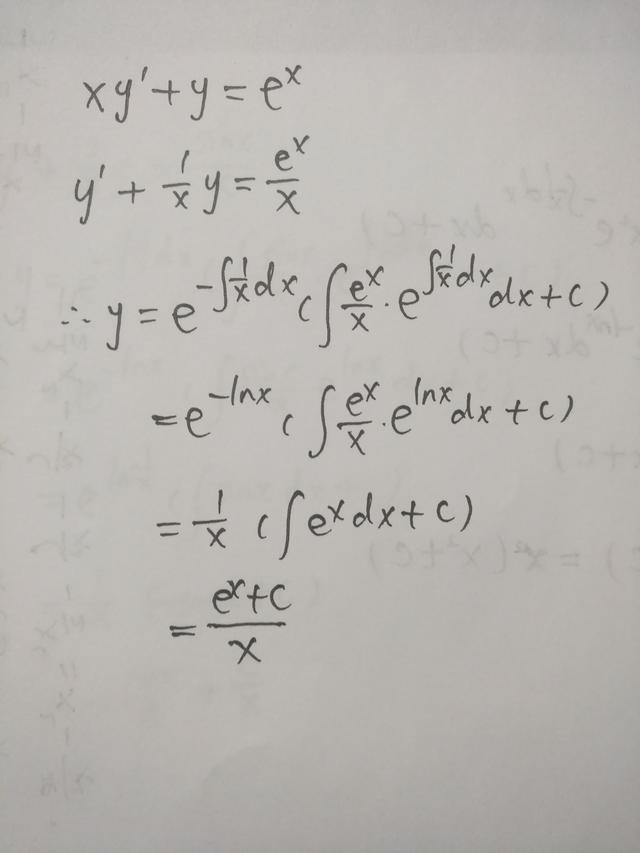
本例中，先要将y'前面的系数x变形除后，得到：p(x)=1/x，q(x)=e^x/x.

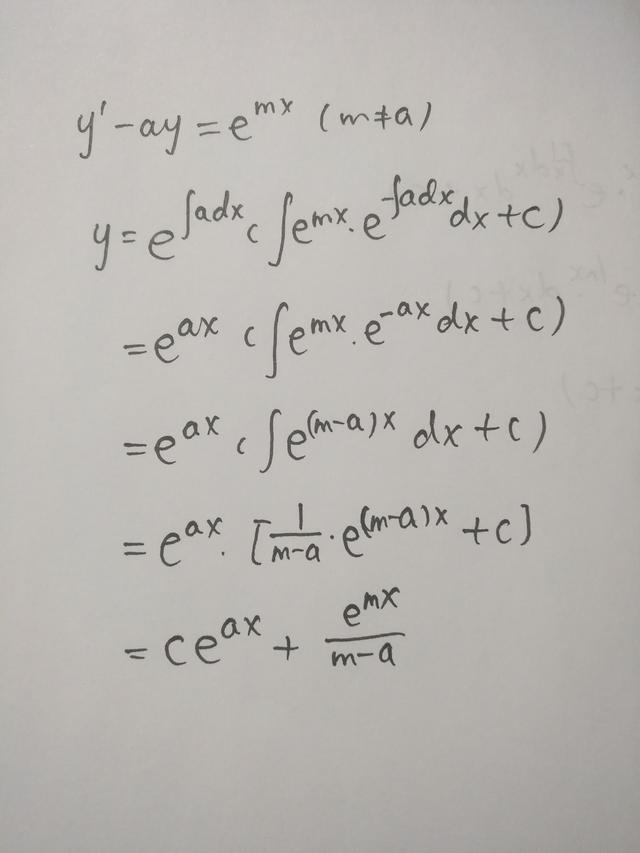
本例中，p(x)=-a，q(x)=e^mx.

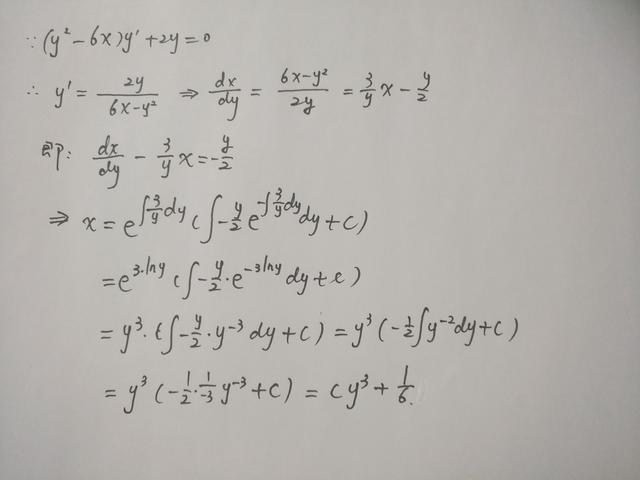
此例中，要反过来用一阶非齐次线性微分方程的通解公式，其中：p(y)=-3/y，q(y)=-y/2.

三、用公式求特解情况举例

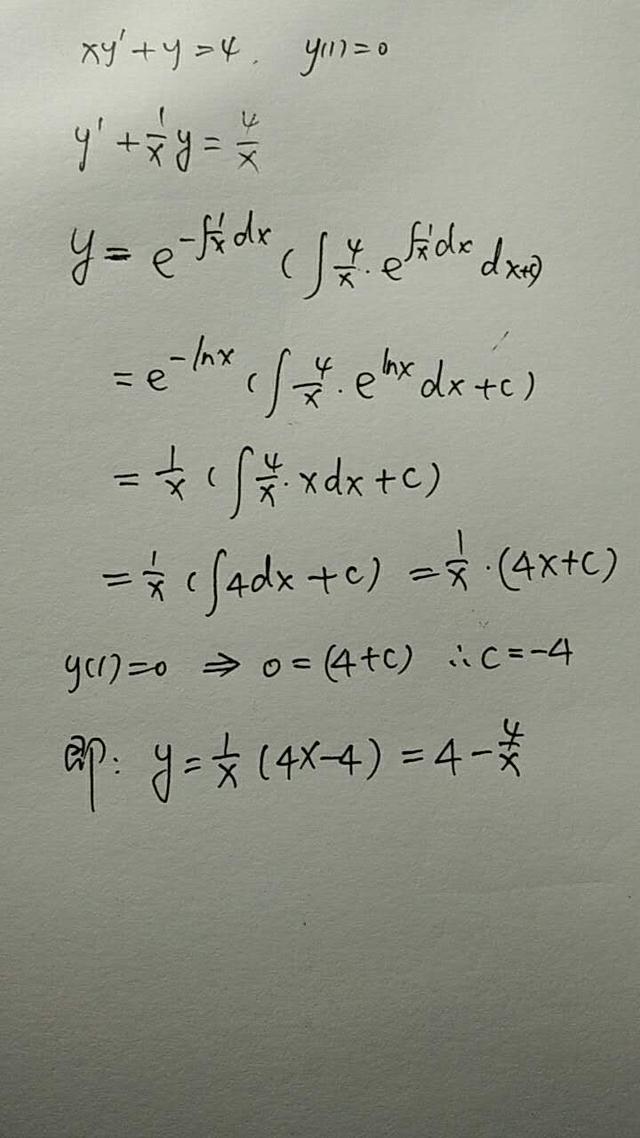
本例中p(x)=1/x，q(x)=4/x，求满足y(x=1)=0时的特解。

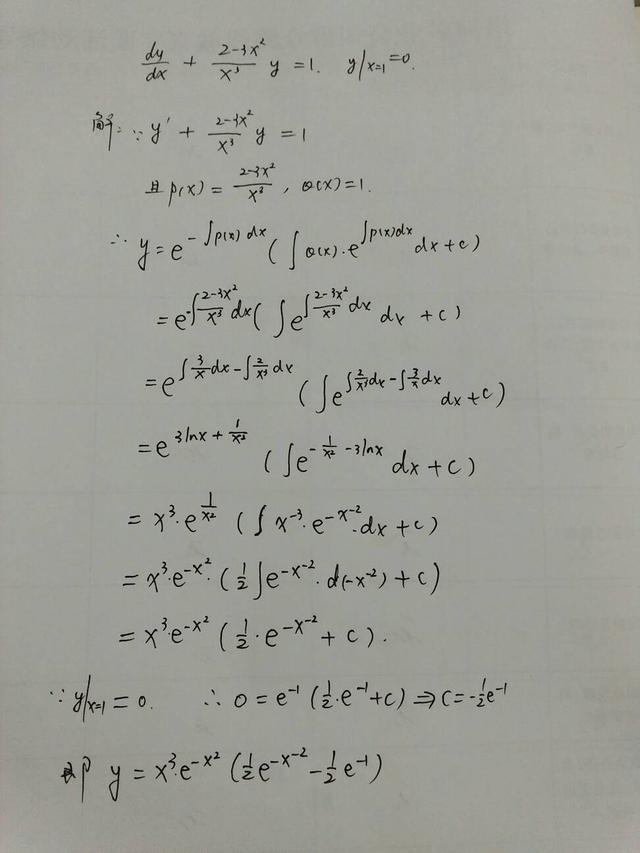
本例中p(x)=(2-3x^2)/x^3，q(x)=1，求满足y(x=1)=0时的特解。

四、二阶微分方程可使用通式求解举例

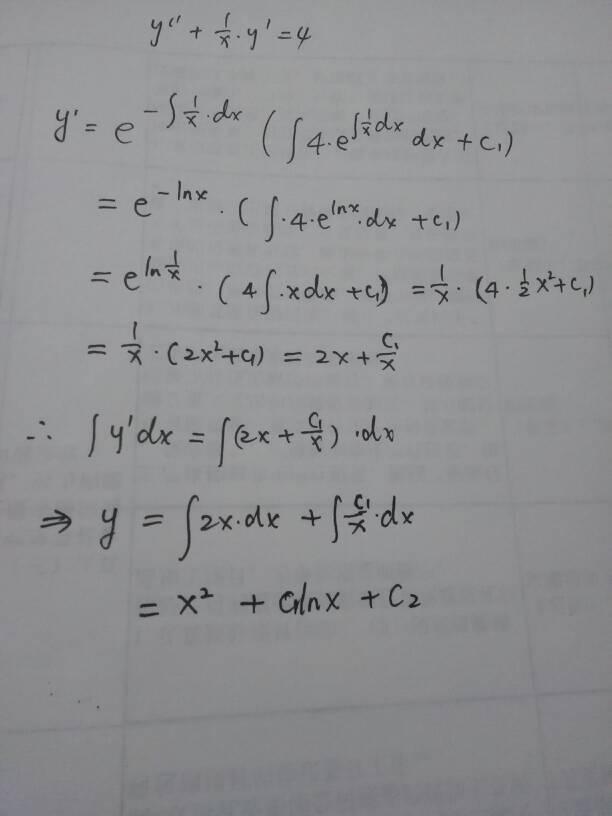
y''+y'/x=4，此时先对y'按照通式公式来求解，再对y'积分求解得到y，通解中含有两个常数系数c1和c2，此时P=1/x，Q=4。

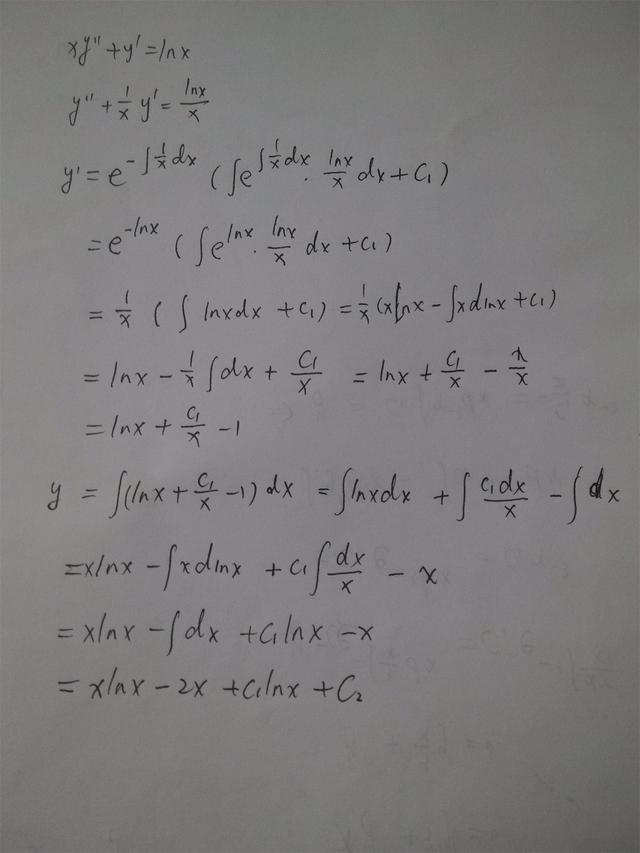
y''=y'+x，此时先对y'按照通式公式来求解，再对y'积分求解得到y，通解中含有两个常数系数c1和c2，此时P=-1，Q=x。

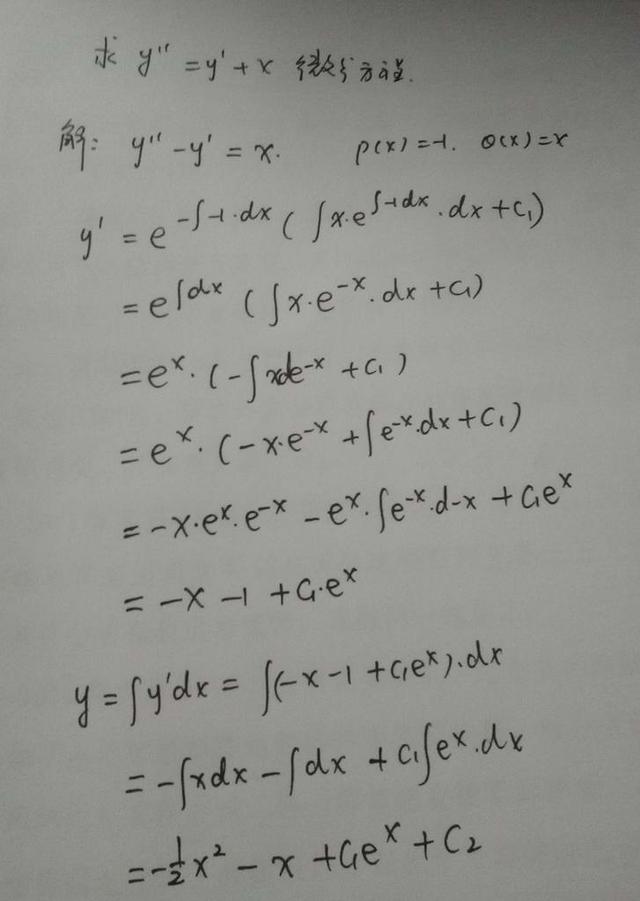
xy''+y'=lnx，此时先对y'按照通式公式来求解，再对y'积分求解得到y，通解中含有两个常数系数c1和c2，此时P=1/x，Q=lnx/x.