c++红黑树（小白慎入）

最新推荐文章于 2025-04-15 18:14:25 发布
最新推荐文章于 2025-04-15 18:14:25 发布
阅读量955 收藏 2
点赞数
分类专栏： C++ 算法 树 文章标签： 算法 c++ 二叉树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_42421684/article/details/106021982
版权
本文介绍了C++实现红黑树的详细过程，包括查找、插入和删除操作。通过实例解析了红黑树的性质和平衡调整策略，如左旋、右旋和颜色调整。并提供了相关操作的代码实现，帮助读者理解红黑树的运作机制。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

这一次我改用c++了，因为我嫌弃java没有指针。。。
写在前面，网上有红黑树插入删除可视化模拟器，可以插入删除规定范围内的数，可以感受感受，尤其是删除

  1. https://sandbox.runjs.cn/show/2nngvn8w
    对于这个网址，亲测无效，不知道你读这篇文章的时候有没有效。
    在这里插入图片描述

  2. 链接：https://pan.baidu.com/s/1_c7juIdNxjBPBSqHDPT7uA
    提取码：4jcn
    这个是我自己上传的，也是从网上找到的，如果有差池，那可能是我上传的出错了。亲测有效。

哈哈，红黑树，听起来好难得样子，其实呢？其实也很难！
啊？！？！
废话不多说，入主题。
您需要准备以下知识点：
二叉搜索树
指二叉树满足：
左子树小于根
右子树大于根
左右子树都是二叉搜索树
示例：
bst
更严格的定义，二叉搜索树的中序遍历是升序的。（其实大家都知道这个，没几个人提到？）
二叉平衡树
满足：
左子树和右子树高度差的绝对值不大于1
左右子树都是二叉平衡树
以下这一棵树严重畸形（不平衡）：
畸形树
对于二叉搜索树，我原来就有一点不太明白。比如当b>a时，b是当a的右子节点还是a当b的左子节点？对效率有影响吗？（这里先埋一个伏笔，很深）
有时候有。如果正好形成了一颗畸形树，将会非常非常慢，退化成链，当搜索的时候，一点一点爬，比蜗牛还慢。。。。
如果能保持平衡，那基本就是O(logn)的复杂度。
怎么保持平衡呢？红黑树登场了。
红黑树应满足：

  1. 每一个节点非黑即红。
  2. 黑土种的树，树根是黑的。
  3. 每一个节点的空子位置都挂着虚拟节点NULL，虚拟节点也是黑的。说明一下，下面画的图大部分没有画出虚拟节点，请打开脑洞，想象那里有一个虚拟节点。
  4. 红节点的每一个孩子必须是黑的（虚拟节点也算孩子呵呵呵）。推论：如果这个节点是红的，它的父亲必定不是红的（否则这个节点就是黑的），说明它的父亲必定为黑色，即父子不能都是红的，不代表黑色不行。
  5. 对于任意一个节点，它到任意一个后代叶子节点的路线中黑色节点相同。
  6. 红黑树是二叉搜索树，接近二叉平衡树。
  7. 有黑子，必有两个子。

好复杂鸭鸭！！怎么那么难？？嘿嘿(●ˇ∀ˇ●)，还没到最难的地方呢。。。
啥？！？！
举个栗子吧
我举个例子
栗子

到这里了，大家应该了解红黑树的性质了吧，现在我们就要鼓捣鼓捣各种操作了。。。
哦！！对了，还有“伏笔”呢，这里说明一下吧：
其实在二叉搜索树里，a的右子节点是b，而变成b的左子节点是a的这一步，叫做对a节点左旋
那这下子b原来的左子节点c交给谁管呢？那就交给a管吧，当它的右子节点。
其实可以想象为c先连接a，然后断开和b的连接，提起来b，就完成左旋了。这时候你会发现左旋并不破坏原有的搜索树性质，只会更改平衡性质（可能是变好也可能是变坏）。
上图吧：
左旋
右旋就是正好反过来，对于左旋，一切“左”变成“右”，一切“右”变成“左”，（连名字都遵循这规矩），就是右旋了。
以下段落为替换出来的结果：

其实在二叉搜索树里，a的左子节点是b，而变成b的右子节点是a的这一步，叫做对a节点右旋
那这下子b原来的右子节点c交给谁管呢？那就交给a管吧，当它的左子节点。
其实可以想象为c先连接a，然后断开和b的连接，提起来b，就完成右旋了。这时候你会发现右旋并不破坏原有的搜索树性质，只会更改平衡性质（可能是变好也可能是变坏）。

哈哈，其实我也挺懒的，直接替换就行了（顺便提一下，这里替换是有技巧的，三变量交换。左替换成哈喽，右替换成左，哈喽替换成右哈哈哈）
又跑题了。右旋也上个图吧：
右旋
还有一种叫变色，就是把颜色变一下（变成你想要的颜色），很容易理解吧。。。

现在鼓捣操作：

操作

查找

查找其实和二叉搜索树一样：

注意！这些函数都是在类Node里面的！

T find(K ky){
   if(key==ky)return data;//命中目标 
   else if(ky<key && left != NULL)return left->find(ky);
   else if(ky>key && right != NULL)return right->find(ky);
   else return NULL;//失败 
  }

因为红黑树是平衡的，所以复杂度也就差不多lgn，不会太慢，这背后的一切……
都是插入删除在不停的维护平衡啊！！！

插入

插入首先要找到要插入的位置。
和查找差不多。

void InsFix(Node* n){
   
  }
  bool insert(Node* node){
   if(key==node->key){//更新 
    data=node->data;
    return true;
   }
   bool res=false;
   if(node->key < key){//实际比当前小，往左走 
    if(left != NULL)res=left->insert(node);
    else{
     left=node;node->fa=this;
    }
   }else{//实际比当前大，往右走 
    if(right != NULL)res=right->insert(node);
    else{
     right=node;node->fa=this;
    }
   }
   InsFix(node); 
   return res;
  }

要插入什么颜色呢？当然是红色，因为红色不会太破坏平衡，能不破坏就不破坏。相反地，黑色特别容易破坏平衡，怪不得是黑色呢（联想一下黑客，就知道为什么是黑色了）。
InsFix是什么呢？就是要修补不平衡的情况：
其实这些情况是在插入函数内完成的：

1.树是空树：

设为根节点，并把颜色设为黑色
其实呢，这一种情况没有显式地表现出来。
调用insert的时候，必须有一个节点（有一个节点就不是空树了！！），使用它来调用insert，在子树插入。
此时，其实树不是空树。
那什么时候会出现这一种情况呢？
在这时：
Node* node;
默认就是黑色的（你可以指定它是黑色的，到文末代码部分时就会明白），所以它还是隐式地体现的。

2.节点已存在：

刷新数据

3.父节点为黑色（默认）：

插入。

接下来要在InsFix实现：

4.父节点是红节点：

现在已经明显不符合性质4（红之子必黑）了。就需要修补了：

4.1.叔叔有并为红色：

4.1这是其中一种情况，还有的其实都一样，叔叔和爸爸变黑，爷爷变红。

这下得麻烦祖辈搞一搞平衡的事情了。。。
上面有个问题，如果爷爷是根肿么办？
那就把他的颜色硬拉回黑的呗，也不会破坏平衡，为什么？
假设会，说明是对于太爷爷，左子方向多了一个黑，右子没多黑，就不平衡了。
嗯？？？不是说好的爷爷就是首代了吗，还有爹？这个爷爷已经是女娲捏出来的了，真的不存在所谓的“太爷爷”了！
所以矛盾（在反证的时候最喜欢说矛盾二字了哈哈哈）
哈哈，不用管喽！！！😜○( ＾皿＾)っHiahiahia…

4.2.叔叔无或为黑：

为了精简，以下4.2.n为：
说明
上面一个标号的节点表示当前插入后的节点，它的标号n代表这个位置会在4.2.n说到

4.2.0

4.2.0
爹变黑，爷爷变红，对爷爷右旋。
其实自己（刚插入的节点）变黑在右旋也行，只不过不想在找祖辈麻烦了~~
如果麻烦了，等着T飞就对了<(￣︶￣)↗[GO!]

4.2.1

4.2.1
其实后面的部分是Ctrl+CV过来的，添加了点东西而已ο(=•ω＜=)ρ⌒☆
对b左旋，InsFix(b)就OK了。

4.2.3

啊啊啊啊？？？？怎么0，1，蹦到3了？？应该是2吧。难道是打错了？？
NO！因为4.2.2是基于4.2.3的，所以先来这个(✿◕‿◕✿)
(⊙_⊙)？
(⊙﹏⊙)
没见过数数这么数的鸭。。。
0，1，3？？？！！！！！！
Pia!(ｏ ‵-′)ノ”(ノ﹏<。)
4.2.3
爸爸变黑，爷爷变红，对爷爷左旋。

4.2.2

呵呵，这回回到2了。
4.2.2
对b右旋，InsFix(b)，OK。
插入情景完~~
．<{=．．．．
灵魂拷问，你真的理解了吗？
来一道题吧。。。加深印象

do{
	读一遍所有插入情景;
}while(!会做题);

习题
答案
最后贴上代码：

void leftturn() {
		Node* myfa = fa;
		Node* rl = right->left;
		fa = right;
		right->left = this;
		right->fa = myfa;
		if (myfa != NULL) {
			if (myfa->left == this)myfa->left = right;
			else myfa->right = right;
		}
		right = rl;
		if (rl != NULL)right->fa = this;
	}
	void rightturn() {
		Node* myfa = fa;
		Node* lr = left->right;
		fa = left;
		left->right = this;
		left->fa = myfa;
		if (myfa != NULL) {
			if (myfa->left == this)myfa->left = left;
			else myfa->right = left;
		}
		left = lr;
		if (lr != NULL)left->fa = this;
	}
	void InsFix(Node* n) {
		if (n->fa->color == true) {
			Node* l = n->fa->fa->left;
			Node* r = n->fa->fa->right;
			Node* uncle = (l == n->fa ? r : l);
			if (uncle == NULL || uncle->color == false) {//叔叔黑 
				int c = ((n->fa->fa->right == n->fa) << 1) + (n->fa->right == n);//判断情况
				switch (c) {
				case 0:
					n->fa->color = false;//爸爸变黑
					n->fa->fa->color = true;//爷爷变红
					n->fa->fa->rightturn();//爷爷右旋
					break;
				case 1:
					n->fa->leftturn();//爸爸左旋
					InsFix(n->left);//再做case0处理
					break;
				case 2:
					n->fa->rightturn();//爸爸右旋
					InsFix(n->right);//再做case3处理
					break;
				case 3:
					n->fa->color = false;//爸爸变黑
					n->fa->fa->color = true;//爷爷变红
					n->fa->fa->leftturn();//爷爷左旋
					break;
				}
			}
			else if (uncle->color == true) {//叔叔是红的
				n->fa->fa->left->color = false;
				n->fa->fa->right->color = false;//把爷爷的两个孩子（必有一个爸爸和一个叔叔）都设成黑色的
				if (n->fa->fa->fa != NULL)
				{

					n->fa->fa->color = true;
					InsFix(n->fa->fa);
				}

			}
		}
	}
	bool insert(Node* node) {
		if (key == node->key) {//更新 
			data = node->data;
			return true;
		}
		bool res = false;
		if (node->key < key) {//实际比当前小，往左走 
			if (left != NULL)res = left->insert(node);
			else {
				node->color = true;
				left = node; node->fa = this;
				InsFix(node);
			}
		}
		else {//实际比当前大，往右走 
			if (right != NULL)res = right->insert(node);
			else {
				node->color = true;
				right = node; node->fa = this;
				InsFix(node);
			}
		}
		return res;
	}

如果你跳出来了那个dowhile循环（见上文），恭喜你，你将会迎来新的循环（在后面），但保证新的循环是最后一个了。。。
插入是不是很复杂？哈哈哈，还有更难的。但别跑哦
别跑
，胜利就在前方！！

删除

这将会是全文最难的部分，各位看官要留一留神了，一不小心就会晕倒（难晕了(((φ(◎ロ◎;)φ)))），注意休息。。
网上都这么说：

删除节点就相当于删除替代节点

我看了差不多可以说是一脸懵？？？一会又后继节点，一会又不后继节点的，真的好晕乎啊。。。(⊙﹏⊙)
梳理一下吧：

  1. 为什么要替代节点？
    想一下就知道，如果把一个上有老下有小的中年油腻男给干掉了，老和小怎么连接吧？？

  2. 谁来替代？
    别人说的后继节点替代，我就想知道难道要删孙子爷爷来替代？？？
    所以！更确切地来说，是这样找替代的（有点复杂呦呦呦）：
    case 1:没有子节点
    平衡一下，就扔掉节点就完了。
    case 2:一个子节点
    用子节点替代
    然后让它找替代。
    case 3:两个子节点
    右节点替代。如果右节点有左子节点，一直向左找，找到尽头。
    找到替代节点后把数据拷过来，然后在让它自己去找替代，找不着就是自爆。

这个涉及到递归，真的好复杂。。。╯︿╰
这个是一个很容易。。。。。。。出错的部分，也许本小白也出错了。。。

bool DelFix() {

	}
	bool remove() {
		Node* r = this;
		int counter = 0;
		int wh = 0;
		if (left != NULL)counter++, wh++;
		if (right != NULL)counter++, wh += 2;
		switch (counter) {
		case 0:
			if (fa == NULL) { return true; }//NP
			DelFix();
			if (this == fa->left)fa->left = NULL;
			else fa->right = NULL;
			//(this == fa->left ? fa->left : fa->right) = NULL;
			//为何还认原来的爹是因为很可能需要用这个节点找根节点，如果要插入到其他地方爹会改的。。。
			break;
		case 1:
			r = (wh == 1 ? left : right);
			//if (r == NULL)throw "12345";
			key = r->key;
			data = r->data;
			r->remove();
			break;
		case 2:
			r = right;
			while (r->left != NULL)
			{
				r = r->left;
			}
			key = r->key;
			data = r->data;
			r->remove();
			break;
		}
		return false;
	}
	
	Node *del(K ky,bool &dd) {
		dd = false;
		if (key == ky) {
			dd=remove();
			return this;
		}//命中目标 
		else if (ky < key && left != NULL)return left->del(ky,dd);
		else if (ky > key&& right != NULL)return right->del(ky,dd);
		else return NULL;//失败 
	}

好了，希望大家能够理解吧（确实有点难o_o …）
下面正式进入各种情景部分。

1.删除红色节点

四个字：运气太好！恭喜你，复杂情况暂时告别你了○( ＾皿＾)っHiahiahia…直接删除就行liao！

2.删除黑色节点

这才是正常情况，运气一般般。

2.1删除节点是长子
2.1.1 兄弟是红色的

2.1.1

把兄弟变成黑色，爸爸变成红色，对爸爸左旋，得到后面情景。
这里是其中一种，其实不确定到底后面哪一个情况。。。
对于这一种，这里有一个问题。a如果是虚拟的怎么办？其实不标红就行了。为啥？如果原来这里就不存在，你会发现把要删除的节点直接删除了就可以了。这时实际上（指不算虚拟节点），原来删除节点的爸爸已经没有子节点了，此时啥都完事了。从祖辈到那个爸爸就是头了，已经下不去了，所以就完了。

嗯？(⊙o⊙)？这个。。。不平衡鸭鸭鸭！！
你忘啦？不是一会要删除的嘛嘛，怎么就不算帐了额。。
如果删了，你会发现恢复了平衡。
如果不删，那就是不删的问题了。

2.1.2 兄弟是黑的
2.1.2.1 右侄子红色

2121
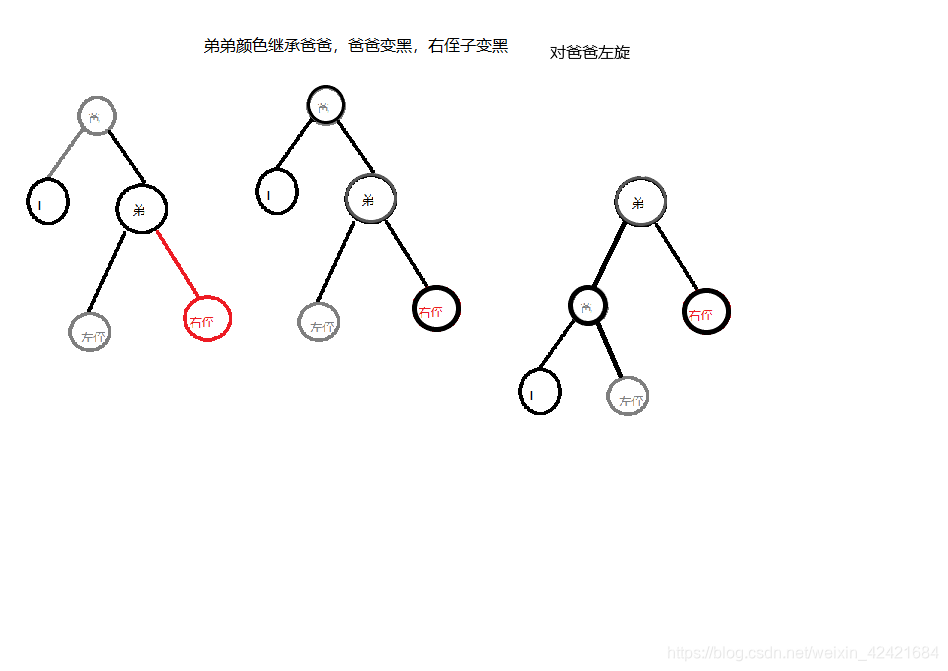
弟弟颜色变成爸爸的，爸爸变黑，右侄子变黑。对爸爸左旋。

2.1.2.2 右侄子黑色，左侄子红色。

2.1.2.2
这个只需要把左侄子变黑，弟弟变红，然后对弟弟右旋，得到上一个情景。

2.1.2.3侄子全是黑的

这下怎么办呢？有一点复杂，又分出岔路来了。
首先左边少了一个黑的，右边也该少一个吧，先把弟弟涂红。

2.1.2.3.1 爸爸是红色的

这个其实就是上面所谓的“后面情景”。当然了。。也可能不是这个情景(￣▽￣)"。别看情景号码长，这个甚至可以号称黑色最简情景！根本用不着旋转。其实麻烦的在后面呢，
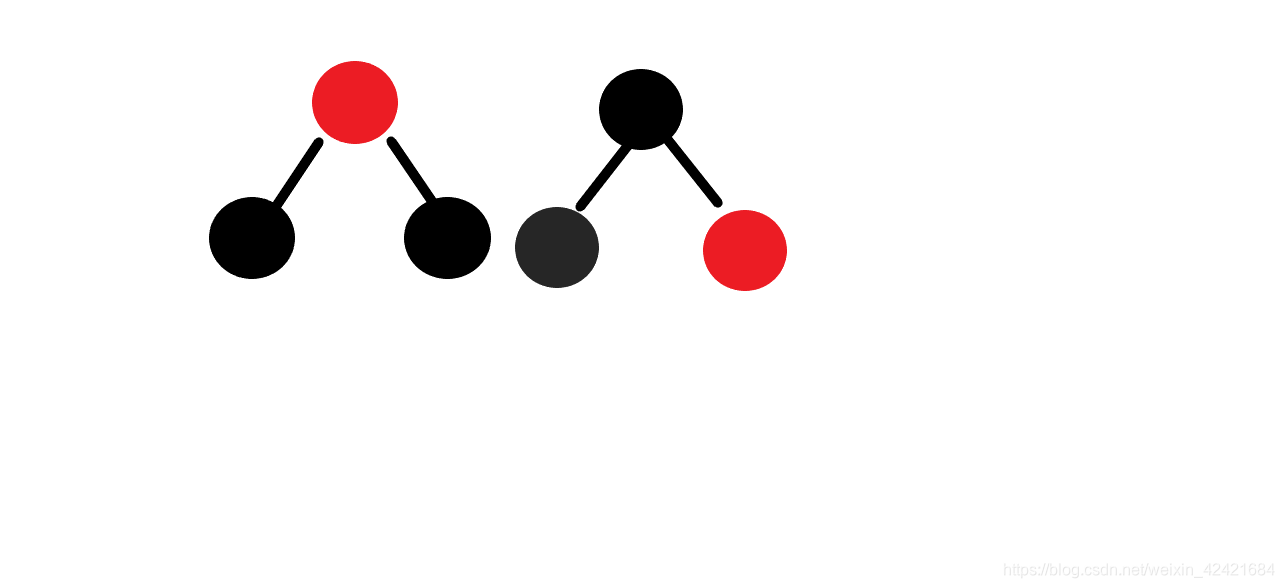
2.1.2.3.1
想一想，当兄弟涂红后，左边消失后，谁来继承黑色大业（否则爸爸这一边少了个黑色）？只能爸爸反继承了。所以要把爸爸标黑。此时就完了。（￣︶￣）↗

2.1.2.3.2 爸爸是黑色的

此时四个字，运气太差！这时要找祖先了。在弟弟标红后，就该找爸爸，再做平衡了。如果找到了根节点，那没有弟弟了，就退出就对了。
2.1.2.3.2
你以为删除就这么完了？？太天真了！！还没考虑是爸爸的次子呢！

2.2 删除节点是次子

其实说实话，这就是给反过来而已。。。也差不多了，为了省事，就不贴图了。。。(✿◕‿◕✿)
如果不明白，看我不一定靠谱の代码。

2.2.1兄弟节点红色

记得原来怎么弄的吗？现在改一下：哥哥变黑，爸爸变红，爸爸右旋。重新处理。

2.2.2 兄弟节点黑色
2.2.2.1 左侄子红色

哥哥颜色变成爸爸的，爸爸变黑，左侄子变黑。对爸爸右旋。

2.2.2.2 左侄子黑色，右侄子红色

右侄子变黑，哥哥变红，对哥哥左旋，得到上面情景↑。

2.2.2.3 侄子皆黑

哥哥先变红。

2.1.2.3.1 爸爸是红色的

爸爸标黑。

2.1.2.3.2 爸爸是黑色的

找爸爸。

啊！！删除终于地玩完了！！
φ(゜▽゜*)♪
[]~(￣▽￣)~*<
(￣︶￣)↗[GO!]
(●’◡’●)


	void DelFix() {
		if (fa == NULL)return;//找到根节点，没得玩了。
		else if (color)return;//中了一个亿彩票大运
		else {
			//吃亏常态
			if (this == fa->left) {//长子
				if (/*(fa->right != NULL) && */fa->right->color == true) {
					fa->color = true;
					fa->right->color = false;
					fa->leftturn();
					//fa->color = false;
					//if (fa->right != NULL)fa->right->color = true;
					DelFix();//重新判断情景。
				}
				else {
					if ((fa->right->left == NULL || fa->right->left->color == false)
						&&
						(fa->right->right == NULL || fa->right->right->color == false)
						)
					{
						fa->right->color = true;
						if (fa->color) {
							fa->color = false;
						}
						else {
							fa->DelFix();
						}
					}
					else if ((!(fa->right->right == NULL)) && fa->right->right->color == true) {
						fa->right->color = fa->color;
						fa->color = false;
						fa->right->right->color = false;
						fa->leftturn();
					}
					else if ((fa->right->right == NULL || fa->right->right->color == false) && fa->right->left->color == true) {
						fa->right->left->color = false;
						fa->right->color = true;
						fa->right->rightturn();
						fa->right->color = fa->color;
						fa->color = false;
						//if (fa->right->right == NULL)throw "123456";
						fa->right->right->color = false;
						fa->leftturn();

					}
				}
			}
			else {
				if (/*(!(fa->left == NULL)) && */fa->left->color) {
					fa->left->color = false;
					fa->color = true;
					fa->rightturn();
					DelFix();//重新判断情景。
					//fa->color = false;
					//if (fa->left != NULL)fa->left->color = true;
				}
				else {
					if ((fa->left->right == NULL || fa->left->right->color == false)
						&&
						(fa->left->left == NULL || fa->left->left->color == false)
						) {
						fa->left->color = true;
						if (fa->color == true) {
							fa->color = false;
						}
						else {
							fa->DelFix();
						}
					}
					else if((!(fa->left->left == NULL)) && fa->left->left->color)
					{
						fa->left->color = fa->color;
						fa->color = false;
						fa->left->left->color = false;
						fa->rightturn();
					}
					else {
						fa->left->right->color = false;
						fa->left->color = true;
						fa->left->leftturn();
						fa->left->color = fa->color;
						fa->color = false;
						//if (fa->left->left == NULL)throw "234";
						fa->left->left->color = false;
						fa->rightturn();
					}
				}
			}
		}
	}
	bool remove() {
		Node* r = this;
		int counter = 0;
		int wh = 0;
		if (left != NULL)counter++, wh++;
		if (right != NULL)counter++, wh += 2;
		switch (counter) {
		case 0:
			if (fa == NULL) { return true; }//NP
			DelFix();
			if (this == fa->left)fa->left = NULL;
			else fa->right = NULL;
			//(this == fa->left ? fa->left : fa->right) = NULL;
			//为何还认原来的爹是因为很可能需要用这个节点找根节点，如果要插入到其他地方爹会改的。。。
			break;
		case 1:
			r = (wh == 1 ? left : right);
			//if (r == NULL)throw "12345";
			key = r->key;
			data = r->data;
			r->remove();
			break;
		case 2:
			r = right;
			while (r->left != NULL)
			{
				r = r->left;
			}
			key = r->key;
			data = r->data;
			r->remove();
			break;
		}
		return false;
	}
	
	Node *del(K ky,bool &dd) {
		dd = false;
		if (key == ky) {
			dd=remove();
			return this;
		}//命中目标 
		else if (ky < key && left != NULL)return left->del(ky,dd);
		else if (ky > key&& right != NULL)return right->del(ky,dd);
		else return NULL;//失败 
	}

嘿嘿(●ˇ∀ˇ●)，我玩完了你还没呢(●’◡’●)，题等着你○( ＾皿＾)っHiahiahia…
对于不理解的各位，请务必要做一做。

do{
 读一遍所有删除情景;
}while(!会做题);

d习题
答案戳我
趁着热乎，赶紧用红黑树做一道题吧：

问题描述

你有一个盒子，可以扔一个数进去，也可以拿出来一个。

最开始，盒子空空如也，你会做 Q 个操作，操作分为两类：

插入操作：先看一看盒子有没有数 x，如无就把数 x 扔进盒子。

删除操作：看一看盒子有没有数 x，如果有取出 x。

每一个操作，你要输出是否成功执行操作。

输入

第一行一个正整数 Q。

接下来 Q 行描述每个操作。每行 2 个用空格隔开的非负整数 op,x 表述一个操作：op 说明插入还是删除，op=1
则表示这是一个插入操作，op=2 则表示这是一个删除操作

输出

按序对每一个操作输出，每个操作输出一行。如成功则输出Succeeded，否则输出Failed。

样例输入

6
1 100
1 100
2 100
1 200
2 100
2 200

样例输出

Succeeded
Failed
Succeeded
Succeeded
Failed
Succeeded

这样一道题，我选择哈希表。用红黑树解决冲突。也许麻烦了。。。

// NumBoxRedBlackTree.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//
#pragma warning(disable : 4996)
#define _OJ_
#include <bits/stdc++.h>
using namespace std;
template<class K, class T>
class Node {
public:
	bool color = false;//黑色是false红色是true。默认刚刚创建的是根节点，所以是黑色。 
	Node* fa = NULL;
	Node* left = NULL;
	Node* right = NULL;
	K key;
	T data;
	Node() {

	}
	Node(K ky, T dat) {
		key = ky;
		data = dat;
	}
	T find(K ky) {
		if (key == ky)return data;//命中目标 
		else if (ky < key && left != NULL)return left->find(ky);
		else if (ky > key&& right != NULL)return right->find(ky);
		else return NULL;//失败 
	}
	inline Node* root() {
		Node* res = this;
		while (res->fa != NULL)res = res->fa;
		return res;
	}
	void leftturn() {
		Node* myfa = fa;
		Node* rl = right->left;
		fa = right;
		right->left = this;
		right->fa = myfa;
		if (myfa != NULL) {
			if (myfa->left == this)myfa->left = right;
			else myfa->right = right;
		}
		right = rl;
		if (rl != NULL)right->fa = this;
	}
	void rightturn() {
		Node* myfa = fa;
		Node* lr = left->right;
		fa = left;
		left->right = this;
		left->fa = myfa;
		if (myfa != NULL) {
			if (myfa->left == this)myfa->left = left;
			else myfa->right = left;
		}
		left = lr;
		if (lr != NULL)left->fa = this;
	}
	void InsFix(Node* n) {
		if (n->fa->color == true) {
			//if (n->fa->fa == NULL)throw "1234";
			Node* l = n->fa->fa->left;
			Node* r = n->fa->fa->right;
			Node* uncle = (l == n->fa ? r : l);
			if (uncle == NULL || uncle->color == false) {//叔叔黑 
				
				int c = ((n->fa->fa->right == n->fa) << 1) + (n->fa->right == n);//判断情况
				switch (c) {
				case 0:
					n->fa->color = false;//爸爸变黑
					n->fa->fa->color = true;//爷爷变红
					n->fa->fa->rightturn();//爷爷右旋
					break;
				case 1:
					n->fa->leftturn();//爸爸左旋
					InsFix(n->left);//再做case0处理
					break;
				case 2:
					n->fa->rightturn();//爸爸右旋
					InsFix(n->right);//再做case3处理
					break;
				case 3:
					n->fa->color = false;//爸爸变黑
					n->fa->fa->color = true;//爷爷变红
					n->fa->fa->leftturn();//爷爷左旋
					break;
				}
			}
			else if (uncle->color == true) {//叔叔是红的
				n->fa->fa->left->color = false;
				n->fa->fa->right->color = false;//把爷爷的两个孩子（必有一个爸爸和一个叔叔）都设成黑色的
				if (n->fa->fa->fa != NULL)
				{

					n->fa->fa->color = true;
					InsFix(n->fa->fa);
				}

			}
		}
	}
	bool insert(Node* node) {
		if (key == node->key) {//更新 
			data = node->data;
			return true;
		}
		bool res = false;
		if (node->key < key) {//实际比当前小，往左走 
			if (left != NULL)res = left->insert(node);
			else {
				node->color = true;
				left = node; node->fa = this;
				InsFix(node);
			}
		}
		else {//实际比当前大，往右走 
			if (right != NULL)res = right->insert(node);
			else {
				node->color = true;
				right = node; node->fa = this;
				InsFix(node);
			}
		}
		return res;
	}
	void DelFix() {
		if (fa == NULL)return;//找到根节点，没得玩了。
		else if (color)return;//中了一个亿彩票大运
		else {
			//吃亏常态
			if (this == fa->left) {//长子
				if (/*(fa->right != NULL) && */fa->right->color == true) {
					fa->color = true;
					fa->right->color = false;
					fa->leftturn();
					//fa->color = false;
					//if (fa->right != NULL)fa->right->color = true;
					DelFix();//重新判断情景。
				}
				else {
					if ((fa->right->left == NULL || fa->right->left->color == false)
						&&
						(fa->right->right == NULL || fa->right->right->color == false)
						)
					{
						fa->right->color = true;
						if (fa->color) {
							fa->color = false;
						}
						else {
							fa->DelFix();
						}
					}
					else if ((!(fa->right->right == NULL)) && fa->right->right->color == true) {
						fa->right->color = fa->color;
						fa->color = false;
						fa->right->right->color = false;
						fa->leftturn();
					}
					else if ((fa->right->right == NULL || fa->right->right->color == false) && fa->right->left->color == true) {
						fa->right->left->color = false;
						fa->right->color = true;
						fa->right->rightturn();
						fa->right->color = fa->color;
						fa->color = false;
						//if (fa->right->right == NULL)throw "123456";
						fa->right->right->color = false;
						fa->leftturn();

					}
				}
			}
			else {
				if (/*(!(fa->left == NULL)) && */fa->left->color) {
					fa->left->color = false;
					fa->color = true;
					fa->rightturn();
					DelFix();//重新判断情景。
					//fa->color = false;
					//if (fa->left != NULL)fa->left->color = true;
				}
				else {
					if ((fa->left->right == NULL || fa->left->right->color == false)
						&&
						(fa->left->left == NULL || fa->left->left->color == false)
						) {
						fa->left->color = true;
						if (fa->color == true) {
							fa->color = false;
						}
						else {
							fa->DelFix();
						}
					}
					else if((!(fa->left->left == NULL)) && fa->left->left->color)
					{
						fa->left->color = fa->color;
						fa->color = false;
						fa->left->left->color = false;
						fa->rightturn();
					}
					else {
						fa->left->right->color = false;
						fa->left->color = true;
						fa->left->leftturn();
						fa->left->color = fa->color;
						fa->color = false;
						//if (fa->left->left == NULL)throw "234";
						fa->left->left->color = false;
						fa->rightturn();
					}
				}
			}
		}
	}
	bool remove() {
		Node* r = this;
		int counter = 0;
		int wh = 0;
		if (left != NULL)counter++, wh++;
		if (right != NULL)counter++, wh += 2;
		switch (counter) {
		case 0:
			if (fa == NULL) { return true; }//NP
			DelFix();
			if (this == fa->left)fa->left = NULL;
			else fa->right = NULL;
			//(this == fa->left ? fa->left : fa->right) = NULL;
			//为何还认原来的爹是因为很可能需要用这个节点找根节点，如果要插入到其他地方爹会改的。。。
			break;
		case 1:
			r = (wh == 1 ? left : right);
			//if (r == NULL)throw "12345";
			key = r->key;
			data = r->data;
			r->remove();
			break;
		case 2:
			r = right;
			while (r->left != NULL)
			{
				r = r->left;
			}
			key = r->key;
			data = r->data;
			r->remove();
			break;
		}
		return false;
	}
	
	Node *del(K ky,bool &dd) {
		dd = false;
		if (key == ky) {
			dd=remove();
			return this;
		}//命中目标 
		else if (ky < key && left != NULL)return left->del(ky,dd);
		else if (ky > key&& right != NULL)return right->del(ky,dd);
		else return NULL;//失败 
	}
	int check() {
		int res = 0;
		if (left != NULL) {
			res += left->check();
			if (left->color == false && right == NULL)throw "RBTER";
			if (color && left->color)throw "RBTER";
		}
		if (right != NULL) {
			int rr = right->check();
			if (rr != res)throw "RBTER";
			//res += rr;
			if (right->color == false && left == NULL)throw "RBTER";
			if (color && right->color)throw "RBTER";
		}
		if (!color)res++;
		return res;
	}
};
//void dfs(Node<int, bool>* st) {
//	if (st == NULL)return;
//	dfs(st->left);
//	cout << (st->key) << " ";
//	dfs(st->right);
//}
typedef long long num;
typedef Node<num, bool>* numcard;
class rbHash {
private:
	const static int p = 202061;//6.1儿童节，我能收到礼物:)，所以挑一个61结尾的哈哈哈
	numcard ns[p];
	inline int hash(num x) {
		int res = abs(x % p);
		return res;
	}
public:
	rbHash() {
		memset(ns, NULL, sizeof(ns));
	}
	void k(numcard n) {
		if (n->left != NULL)k(n->left);
		if (n->right != NULL)k(n->right);
		delete n;
	}
	~rbHash()
	{
		for (int i = 0; i < p; i++) {
			if (ns[i] != NULL)
			{
				k(ns[i]);
			}
		}
	}
	bool insert(num a) {
		int loc = hash(a);
		numcard n = new Node<num, bool>(a, true);
		//if (n == NULL)throw "1324";
		if (ns[loc] == NULL) {
			ns[loc] = n;
			return true;
		}
		else {
			bool r = !(ns[loc]->root()->insert(n));
			ns[loc]->root()->check();
			return r;
		}
	}
	bool find(num a) {
		int loc = hash(a);
		if (ns[loc] == NULL)return false;
		else return ns[loc]->root()->find(a);
	}
	bool remove(num a) {
		int loc = hash(a);
		bool res = true;
		if (ns[loc] == NULL)return false;
		else { 
			numcard wd;
			bool dd;
			//if (ns[loc]->root() == NULL)cout << "uytefuqtewrfuyqtweifryqtweyf";
			//int xxx = (ns[loc]->root()->color);
			numcard x =ns[loc]->root()->del(a,dd); 
			if (dd) { 
				delete ns[loc];
				ns[loc] = NULL;
				return true;
			}
			if (x == NULL)res = false;
			//if(wd != ns[loc])delete wd;
			if (ns[0] != NULL)ns[0]->root()->check();
			return res;
		}
	}
};
void dump(int s) {
	cout << "ohohohhhohohohho";
}
int main() {
	//throw "123456";
	//int datas[] = { 10,40,30,60,90,70,20,50,80,20 };
	//int ddts[] = { 90, 60, 50, 0};
	//Node<int, bool>* nod = new Node<int, bool>(datas[0], true);
	vector<Node<int, bool> > mem;
	//for (int i : datas) {
	//	/*mem.push_back(Node<int, bool>(i, true));*/
	//	Node<int, bool>* n = new Node<int, bool>(i, true);
	//	cout<<i<<" "<<(nod->root()->insert(n))<<" ";
	//}
	//cout << endl;
	//for (int i : ddts) {
	//	cout << i<<" "<<(nod->root()->del(i))<<" ";
	//}
	//cout << endl;
	//dfs(nod->root());
	//signal(SIGSEGV, &dump);
#ifndef _OJ_
	FILE* stream;
	freopen_s(&stream,"C:\\Users\\wangz\\source\\repos\\CDCppDebug\\Debug\\input.txt", "r", stdin);
	freopen_s(&stream,"C:\\Users\\wangz\\source\\repos\\CDCppDebug\\Debug\\output.txt", "w", stdout);
#endif // !_OJ_

	//std::ios::sync_with_stdio(false);
	rbHash *h = new rbHash();
	int q;
	cin >> q;
	for (int i = 0; i < q; i++) {
		int x; num y;
		cin >> x >> y;
		///
		
		///
		try {
			if (x == 1) {
				cout << (h->insert(y) ? "Succeeded\n" : "Failed\n");
			}
			else {
				cout << (h->remove(y) ? "Succeeded\n" : "Failed\n");

			}
		}
		catch (...) {
			cout << i;
			return 0;
		}
	}
	//delete h;
#ifndef _OJ_
	fclose(stdin);
	fclose(stdout);
#endif // !_OJ_

	return 0;
}

// 运行程序: Ctrl + F5 或调试 >“开始执行(不调试)”菜单
// 调试程序: F5 或调试 >“开始调试”菜单

// 入门使用技巧: 
//   1. 使用解决方案资源管理器窗口添加/管理文件
//   2. 使用团队资源管理器窗口连接到源代码管理
//   3. 使用输出窗口查看生成输出和其他消息
//   4. 使用错误列表窗口查看错误
//   5. 转到“项目”>“添加新项”以创建新的代码文件，或转到“项目”>“添加现有项”以将现有代码文件添加到项目
//   6. 将来，若要再次打开此项目，请转到“文件”>“打开”>“项目”并选择 .sln 文件

读了这么多，你应该很好奇吧（我也是），红黑树的发明者的脑洞怎么这么大？？

脑洞
我也是小白，如果有误，请指正！
．<{=．．．．
THE END

参考：
dalao1；
dalao2。

C++_红黑树
安权_code的博客
03-03 1184
在C++中，红黑树是二叉搜索树的另一种优化版本，他与AVL树的区别在于保持树的平衡方式不同，AVL树保持平衡的方式是在节点中多存储一个成员来记录平衡因子，红黑树保持平衡的方式也是增加了一个成员，但是该成员的作用是记录节点的两种状态（颜色）：红色--黑色。当然只记录颜色并不能保持平衡，红黑树还规定最长路径的节点个数不会超过最短路径的节点个数的两倍，因此红黑树不会因为插入有序数据而演变成“单支树”。
C++：二叉搜索树模拟实现（KV模型）
Zhenyu_Coder的博客
02-08 3878
二叉搜索树又称二叉排序树，作为map、set以及红黑树的底层数据结构基础，对于后续模拟实现封装相关解决具体重要意义。同时二叉搜索树分为Key模型和KV模型，在生活中也具有广泛应用，比如英汉字典，通过英文查找对应中文等等。本篇博客将着手二叉搜索树的底层原理，模拟实现二叉搜索树。
C++【红黑树】
芊樱烛渊的博客
11-05 1393
AVLTree：要求左右高度差不超过1红黑树：AVLTree过分严格，可能会导致过分的旋转，那能不能不要那么严格呢？需要达到的目的，最长路径不超过最短路径的二倍。也就是说，我们的AVLTree是严格平衡，我们的红黑树是不严格平衡，而是近似平衡结果：相对而言，插入同样的数据，AVL树的旋转更多，红黑树的旋转次数更少假设N是100w，AVL树为logN的高度，也就是大概20左右但是我们的红黑树的话，最短的高度大概是logN也就是20左右，最深的应该为2*logN，为40次左右。
C++红黑树
最新发布
2401_84068287的博客
04-15 967
如果我们要继续更改父亲变成黑色的话，黑色节点就无法控制了，就是你把f变黑，凭空多出一个黑色节点，用g变红来抵消，但是u的路径上就少了一个黑色节点，但是u本身也是黑色节点无法改变，这时候我们也仔细看一下最长路径已经超过最短路径的2倍了，所以我们要旋转+变色。我们看新增一个红色节点，如果父亲是红色的，那违反规则我们就把它变黑色，但是这条路径多了一个黑色节点，我们要减少一个黑色节点，把6变红，但是6的左边少了一个黑色节点，所有我们把5变黑，这只是最简单的一种情况。
c++：红黑树
2301_79954395的博客
03-19 1707
1.当uncle为红，变色2.当uncle不为红，变色+旋转（1）若parent为左孩子，cur也为左孩子：左旋+变色（2）若parent为右孩子，cur也为右孩子：右旋+变色（3）若parent为左孩子，cur为右孩子：左旋加右旋+变色（4）若parent为右孩子，cur为左孩子：右旋加左旋+变色。
【C++】红黑树
奔赴在热爱征程上的小小孩~
05-14 879
红黑树概念与实现，使用红黑树封装 map 与 set
数据结构课程设计：基于Qt实现的个人通讯录系统及红黑树的实现.zip
06-11
2、本项目适合计算机相关专业(如计科、人工智能、通信工程、自动化、电子信息等)的在校学生、老师或者企业员工下载学习，也适合小白学习进阶，当然也可作为毕设项目、课程设计、作业、项目初期立项演示等。...
C语言底层实现常见数据结构，使用C++中的stl库带你轻松学习数据结构(面向小白)
04-03
而C++的STL中的map和set容器就基于红黑树实现，保证了操作的高效性。 当然，任何高级的数据结构和算法都离不开扎实的基础知识。因此，本课程不会忽视对基础知识点的讲解。从基础的数据结构概念，到算法的时间复杂度...
数据结构-无序（自由）树的简单实现（C++）
W_H_M_2018的博客
09-02 2102
本文使用兄弟孩子表示法用C++实现普通树的简单建立。 实现了插入数据，查询数据，前序遍历，中序遍历，后序遍历。 树状图的概念： 树状图是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。看起来就像一棵倒挂的树。 树状图的特点： 每个结点有零个或多个子结点； 没有父结点的结点称为根结点； 每一个非根结点有且只有一个父结点； 除了根结点外，每个子结...
C++进阶：实现红黑树
QinMou
10-11 796
红⿊树是⼀棵⼆叉搜索树，他的每个结点增加⼀个存储位来表示结点的颜⾊，可以是红⾊或者⿊⾊。 通过对任何⼀条从根到叶⼦的路径上各个结点的颜⾊进⾏约束，红⿊树确保没有⼀条路径会⽐其他路径⻓出2倍，因⽽是接近平衡的。
C++ 红黑树
weixin_53946312的博客
01-28 1658
红黑树
c++——红黑树
蜗@牛的博客
07-10 347
一、红黑树的概念 红黑树是一种二叉搜索树，但是每个结点都有表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出2倍，因而是接近平衡的二叉搜索树。 二、红黑树的特性 1、每个节点要么是黑色，要么是红色。 2、根节点是黑色。 3、每个叶子节点（NIL）是黑色。 4、每个红色结点的两个子结点一定都是黑色。 5、任意一结点到每个叶子结点的路径都包含数量相同的黑结点。 三、红黑树的实现 1、红黑树的插入 （1）根节点为空，则直接插入
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值