第十三章 支持向量机support vector machines SVM

课时101 优化目标

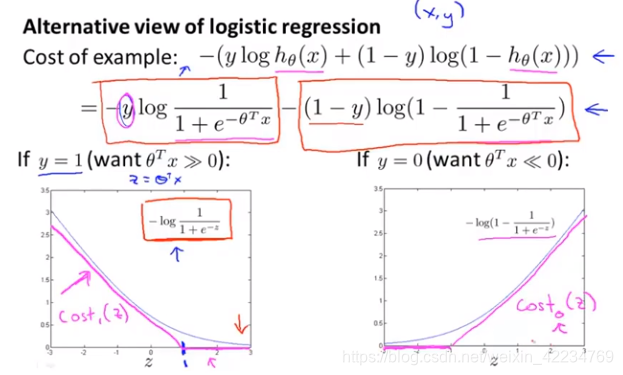
逻辑回归中，记z=θTx。 y=1时，希望z远大于0，代价函数的值由左图的式子决定，可以看出z很大时代价很小。我们将玫红色的线记做cost1(z)。y=0时，希望z远小于0，代价函数的值由右图的式子决定，可以看出z很小时代价很小。我们将玫红色的线记做cost0(z)。
优化目标：

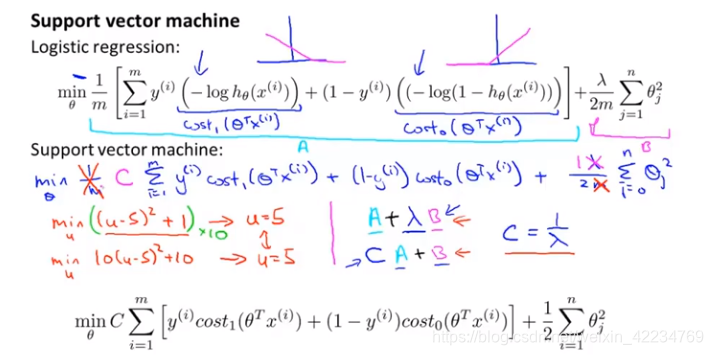
把负号移到了括号里面去了。去掉1/m不影响取最小值的θ值，这里去掉这个常数。把λ变化一下移到前一项，同样在相同的θ处取最值。就得到了最终的优化目标。
与逻辑回归还有一处不同，SVM支持向量机不会输出概率，而是通过学习得出θ后直接预测hθ(x)的结果是0还是1。

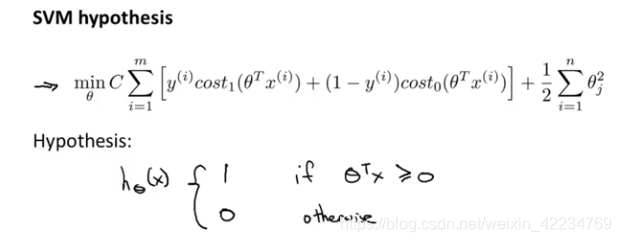
课时102 直观上对大间隔的理解 large margin intuition

这相当于为SVM设置了一个安全间距。当C很大时，我们很希望第一项为0，这时优化目标就变成了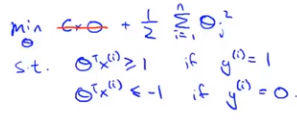结果是：

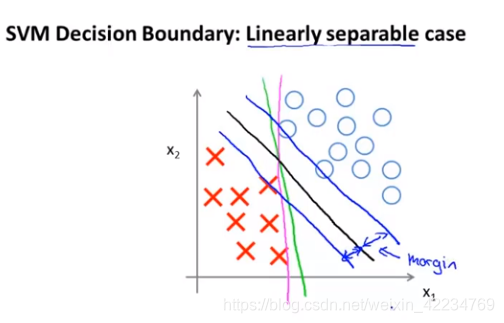
黑线和蓝线的间距就叫margin间距，因此SVM也叫大间距分类器large margin classifier。为什么会这样下一节讲。
现在的大间距分类器是在C很大的情况下实现的，当只使用大间距分类器时你的学习算法对异常点会很敏感。
让C小一点就不会太敏感，可以得到更正确的结果。

课时103 大间隔分类器的数学原理 （optional）从数学上解释为什么C很大时SVM会是大间距分类器
向量内积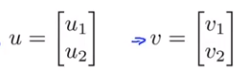：uTv=vTu
算法一：直接算。uTv=u1v1+u2v2.
算法二：投影法。p是将向量v投影到u上的长度(uv夹角大于90度时p就是负的)。内积就是p乘以向量u的长度（范数）。uTv=p·||u||.
见下图，设n=2,有x1 x2, 有θ0 θ1 θ2，设θ0=0。

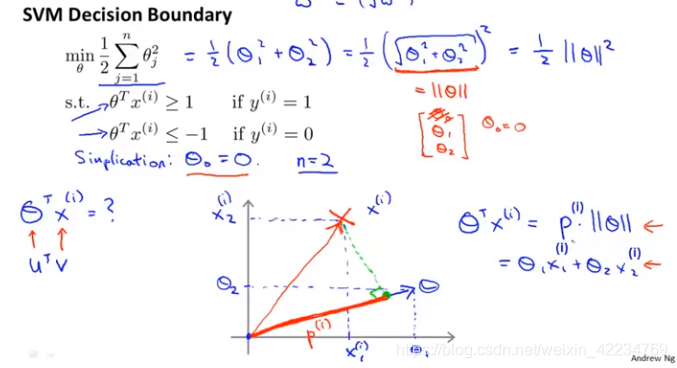
见下图，由代数知识可知boundary和θ垂直。如果不是大间距地分类，如图左，正样本θTx(i)>=1,x的投影p会很短，p小就要求||θ||很大。负样本θTx(i)<=-1,p也短，p是负数值小，要求||θ||很大。与找到使得θ的范式最小的优化目标矛盾了。因此，SVM会尽力找到大间距。

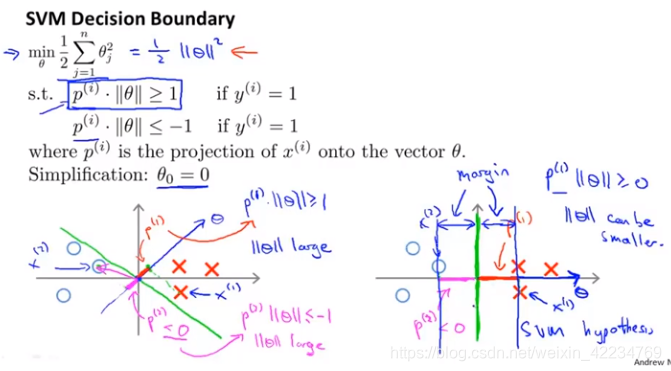
课时104 核函数1 kernels I

f表示特征。
定义新特征的方法：

通过similarity函数表示给定的x与选择的l的接近度，以此来定义新的特征，函数叫核函数（高斯核函数）。

当x与l1接近时，根据核函数的计算式看出f1接近于1；当x于l1离得远时，根据核函数看出f1接近于0。

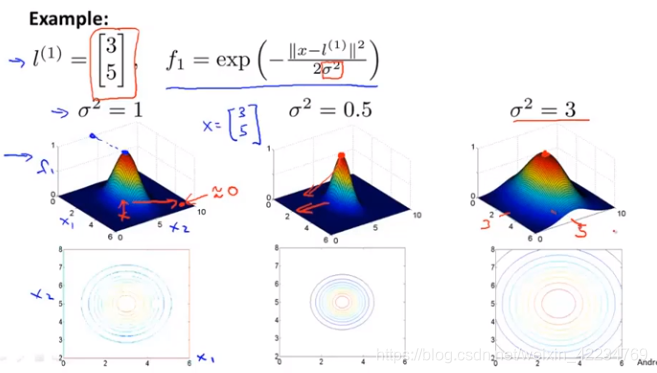
当σ越大，f1函数越平缓。σ越小函数越尖锐。

有了θ，f,便可预测最终结果。

课时105 核函数2 kernels II
选择landmark的方法：
直接将样本点们作为landmark：也就是有m个landmark


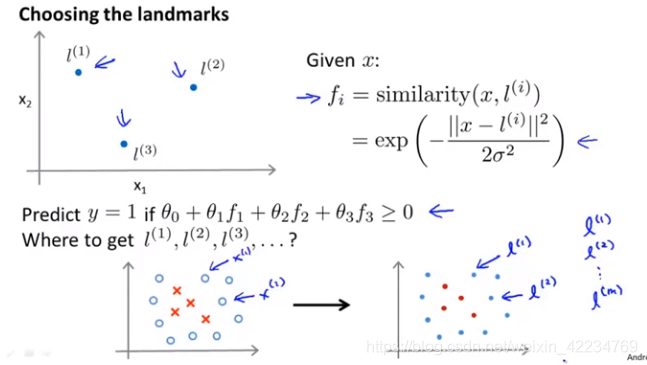
用sim简称similarity函数。对一个给定的x(i)对应的f1(i)到fm(i)，其中有fi(i)就是将这个x(i)点作为了landmark，距离为0，fi(i)为1。f矩阵如上图红色圈圈里面。

最小化的方法可以直接调用包（如liblinear, libsvm, …），不用自己写。但是需要选择参数C和kernel方程。具体见下一节。

选择参数：
大C类似于小λ。
σ2 大σ对应函数平滑，高偏差，欠拟合。

课时106 使用SVM

no kernel/“linear kernel” 没有核参数的函数，假设函数实际上是线性的，适合n大m小，无法拟合比较复杂的函数的时候。
高斯gaussian kernel是最常见的核函数，需要选择σ²，写出函数，提前做feature scaling.

不是所有的相似函数都可以成为有效的核函数，需要满足莫塞尔定理Mercer’s Theroem。 还有一些不常用的核函数：

多类分类：
很多SVM的包已经内置了多分类的函数。或者使用one-vs-all的方法。

逻辑回归和SVM如何选择：