Mobile Robot Posture Stabilization (Regulation)

definition

The $posturestabilization$ problem is to stabilize the vehicle to a desired final posture starting from any initial posture ($posture$ means both the position and the orientation of a mobile robot from base).

difficulty

Posture stabilization problem of wheeled mobile robot is more difficult than the tracking problem in the sense that nonholonomic systems with more degrees of freedom than control inputs cannot be stabilized by any static state feedback control law.

method

The approached for this problem can be largely divided into two categories:

1. open-loop control —— the nonholonomic path-planning
   In the nonholonomic path-planning, authors assume inputs$(v,\varphi )$ in kinematic model as a function of time, then modify the assumed function to fit their purpose.
   However, it is generally difficult to find or modify inputs $v,\varphi$ which transfer a car-like mobile robot to a desired posture and a tracking control should be designed because it is only a path-planning.
2. closed-loop control —— state feedback control
   The most important merit of state feedback control in posture stabilization is that it can be directly used as a controller without any path-planning.

Polar Coordinate-based Stabilizer

It is assumed that, without loss of generality, that the desired configuration is the origin ${\mathbf{q}}_d=[0,0,0{]}^T$

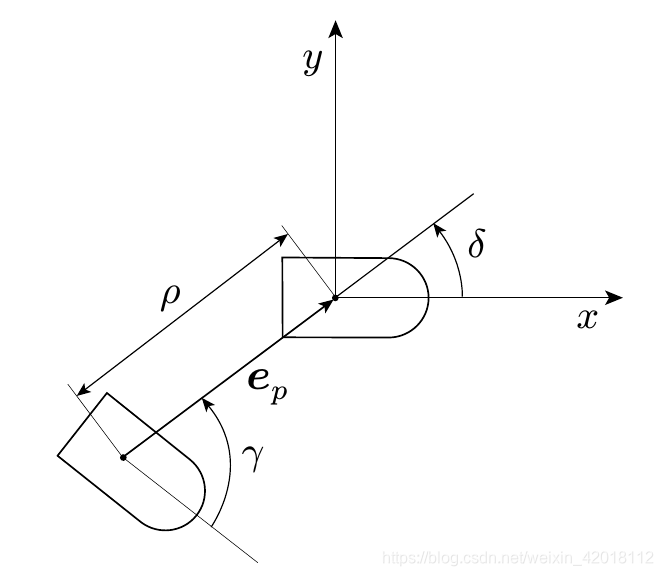
Formulate the problem in polar coordinate:
state representation:
$$\rho =\sqrt{x^2+y^2}$$ $$\gamma =Atan2(y,x)-\theta +\pi$$ $$\delta =\gamma +\theta$$
kinematic model:
$$\dot{\rho }=-vcos\gamma$$ $$\dot{\gamma }=\frac{sin\gamma }{\rho }v-w$$ $$\dot{\delta }=\frac{sin\gamma }{\rho }v$$