逆运动学求解

• 解析法（Analytical Solution）
  顾名思义是用代数或几何方法直接求解。通常随着自由度上升，求得解析解的难度也越来越大，对于冗余机械臂还需要从几个解中选择合适的解。这种方法通常用在特定几何结构的机械臂，并且有特定的关节位置求解顺序。下由于解析解法不具有通用性，我们后面不再详述。
• 优化法（Optimization-based Solution）
  是把问题转化为一个优化问题求数值解。用数学语言说，就是把求
  $$q=f^{-1}(x)$$
  的问题，转化为
  “求关节位置q，使实际end effector位置x与正运动学算出的end effector位置f(q)之间的差最小”的问题：

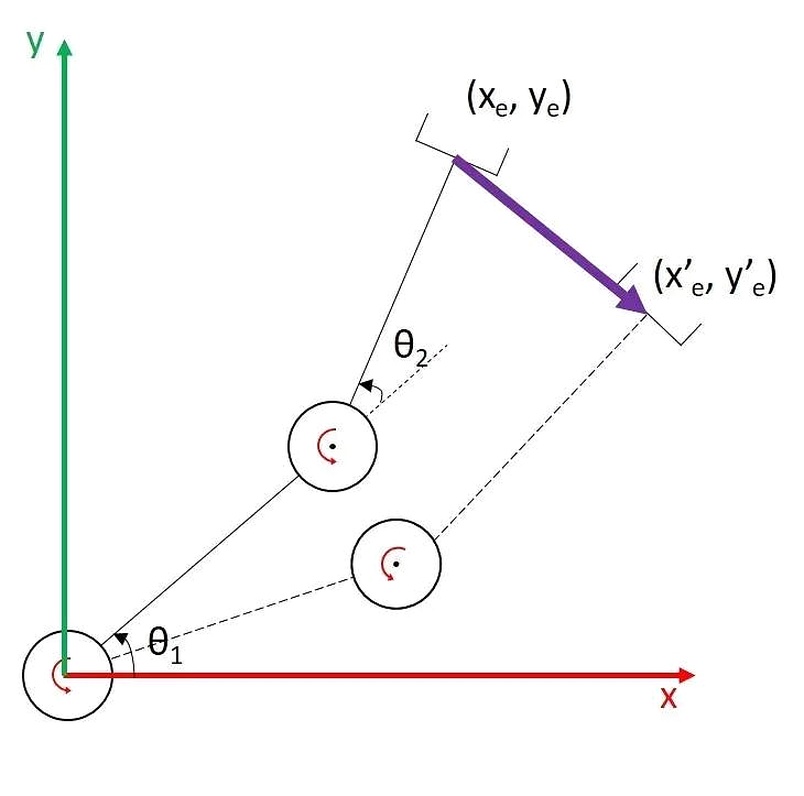
现在我们需要end effector从图中(xe, ye)沿紫色直线移动到(x’e, y’e)，但你需要控制关节位置实现这一点。现在你可以有几种思路——

1. 只求起点和终点对应的关节位置，直接对这两处关节位置进行线性插值求得关节运动轨迹——这样虽然省了很多计算量，但end effector不大可能沿着直线走。
2. 把这条直线插入很多很多中间点，每一个点都求出对应的关节位置，然后控制每一个关节按着这一系列的关节位置走（就是我们前面说的解析/优化解法）。
3. 还是把这条直线插入很多很多中间点，但如果点与点的间隔足够小、运动时间足够短，我们就可以在每一点用雅可比矩阵求逆来求得当前关节位置的变化——换个角度讲，我们也可以设定end effector沿这条直线的运动速度，用雅可比矩阵求逆求得关节速度，直接控制关节的运动速度而不是位置。

第三种方法的控制框图：

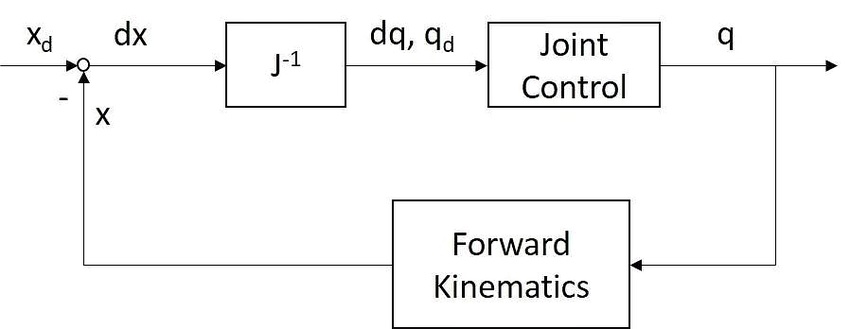
Joint control则是你把你计算出来的$q_{d}$送到每一个关节的控制器中（比如最简单的舵机）；这些控制器最终把各个关节控制到位置$q$（好的控制器，大部分情况$q$和$q_{d}$应当非常接近）。

通常你设置一个$x_{d}$，控制器需要走几遍这个控制回路才能将dx降到接近0（让x逼近$x_{d}$），因此这个方法也被称为迭代法。