范数

        有时我们需要衡量向量的大小，可以使用被成为范数的函数衡量向量的大小。形式上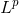，范数定义如下：

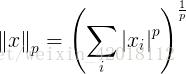
其中。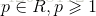

        范数（包括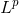范数）是将向量映射到非负值的函数。直观上来说，向量x的范数衡量点x到原点的距离。更严格上来讲，范数是满足下列性质的任意函数：

1. 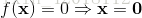                    2. 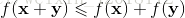(三角不等式)                       3.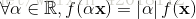

        当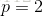时，范数被称为欧几里德范数，它表示从原点出发到向量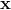确定的点的欧几里德距离。平方范数也经常用来衡量向量的大小，可以简单的通过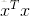计算。

        平方范数在数学和计算上都比范数方便。例如，平方范数对向量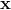中每个元素的倒数只取决于对应的元素，而范数对每个元素的倒数却和整个向量相关。但在某些环境下，平方范数可能并不受欢迎，因为它在原点附近的增长的十分缓慢。在某些环境下，区分零元素和非零但值很小的元素是很重要的。在这些情况下，我们使用在各个位置斜率相同，同时保持简单数学形式的函数：范数。范数形式如下：

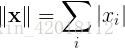
        当某些问题中，零元素和非零元素之间的差异非常重要时，通常会使用范数。每当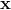中的某个元素从0增加，对应的范数也会增加。

        有时候我们也需要衡量矩阵的大小。最常见的做法是使用Frobenius范数，

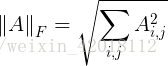
其类似于向量的范数。