Online Meta-Learning2019||论文阅读

 

元学习论文总结||小样本学习论文总结

2017-2019年计算机视觉顶会文章收录 AAAI2017-2019 CVPR2017-2019 ECCV2018 ICCV2017-2019 ICLR2017-2019 NIPS2017-2019

 

---

先简单介绍在线学习的概念：

在线学习算法的特点是：每来一个训练样本，就用该样本产生的loss和梯度对模型迭代一次，一个一个数据地进行训练，因此可以处理大数据量训练和在线训练。常用的有在线梯度下降（OGD）和随机梯度下降（SGD）等

准确地说，Online Learning并不是一种模型，而是一种模型的训练方法，Online Learning能够根据线上反馈数据，实时快速地进行模型调整，使得模型及时反映线上的变化，提高线上预测的准确率。Online Learning的流程包括：将模型的预测结果展现给用户，然后收集用户的反馈数据，再用来训练模型，形成闭环的系统。

Online Learning有点像自动控制系统，但又不尽相同，二者的区别是：Online Learning的优化目标是整体的损失函数最小化，而自动控制系统要求最终结果与期望值的偏差最小。

Online Learning训练过程也需要优化一个目标函数（红框标注的），但是和其他的训练方法不同，Online Learning要求快速求出目标函数的最优解，最好是能有解析解。

一般的做法有两种：Bayesian Online Learning和Follow The Regularized Leader。

---

在线元学习

文章结合了在线学习和元学习的优点。

摘要

智能系统的一个核心能力是能够不断地建立在以前的经验基础上，以加快和加强对新任务的学习。两种不同的研究范式研究了这个问题。元学习把这个问题看作是学习模型参数之上的先验，模型参数能够快速适应新任务，但是通常假设一组任务可以作为一个批处理一起使用。相比之下，在线学习(基于后悔)考虑的是一个顺序设置，在这个设置中，问题一个接一个地暴露出来，但通常只训练一个模型，没有任何特定于任务的适应性。这项工作引入了一个在线元学习设置，它融合了上述两种范式的思想，以更好地捕捉持续终生学习的精神和实践。我们提出“follow the meta leader”算法，将MAML 算法扩展到这个设置。从理论上讲，这项工作提供了一个O(log T)遗憾保证，附加了一个更高阶平滑度的假设(与标准的在线设置相比)。我们对三种不同的大规模任务的实验评估表明，该算法明显优于传统在线学习方法。

介绍

有两种截然不同的研究范式研究了agent如何利用先前的任务或经验来指导未来的学习。Meta-learning (Schmidhuber, 1987; Vinyals et al., 2016; Finn et al., 2017)提出learning to learn,意在从过去的经验中学习超参数以及学习策略的先验信息，通常的做法是提供一系列任务给元学习器学习。另一种办法是在线学习(Hannan, 1957; Cesa-Bianchi & Lugosi, 2006）考虑一个顺序设置，其中任务一个接一个地显示，但目标是在没有任何特定于任务的适应的情况下实现零概率泛化。文章认为，这两种环境都不是研究持续终生学习的理想环境。元学习处理学习的过程，但忽略了问题的顺序和非平稳方面。在线学习提供了一个吸引人的理论框架，但通常不考虑过去的经验如何加速适应新任务。在这项工作中，我们激发并呈现了在线元学习问题设置，其中agent同时在一个连续的设置中使用过去的经验来学习良好的先验，并且快速适应当前手头的任务。

作者举例说明了上述观点。有点绕（例如，图1显示了一系列正弦曲线。我认为每个任务都是一个从x到y的回归问题，对应于一个正弦曲线。当使用来自大量此类任务集合的数据时，不考虑任务结构的朴素方法将集体使用所有数据，并学习与模型y = 0对应的先验。一种理解基本结构的算法会识别出簇中的每条曲线都是一个(不同的)正弦曲线，因此会尝试为新一批数据识别出它所对应的正弦曲线。图1还显示了具有不同背景的彩色MNIST数字，这是另一个关于先前任务的简单训练失败的例子。假设我们已经看到MNIST数字与各种颜色的背景，然后观察一个新的颜色上的7。通过对目前所见的所有数据进行训练，我们可以得出结论，所有颜色的数字都必须是7。事实上，从纯统计的角度来看，这是一个最优的结论。然而，如果我们理解数据被分成不同的任务，并且注意到每个任务都有不同的颜色，那么更好的结论是颜色是无关紧要的。对所有数据进行培训，或者只对新数据进行培训，都不能达到这个目标？？？）

元学习很牛逼，但是需要大量任务数据集。这与真实世界不同，真实世界是现场教学现学现用，在现实世界中，任务可能只是按顺序可用的，就像agent在世界中学习一样，而且是从非平稳分布中学习的。通过在顺序或在线环境中重新定义元学习，我们可以在新任务出现时更快地进行学习

本文的贡献：在这项工作中，我们制定了在线元学习的问题设置，并提出了遵循元领导(FTML)算法。这将MAML算法扩展到在线元学习设置，并对在线学习中的领导者进行了跟踪。我们对FTML进行了分析，结果表明，事后看来，在与最好的元学习者竞争时，FTML具有O(log T)后悔保证。在这项工作中，我们还提供了第一组结果(在任何假设下)，其中类MAML目标函数可以被证明和有效地优化。我们还开发了一种实用形式的FTML，它可以有效地与深度神经网络一起用于大规模任务，并表明它的性能显著优于以前的方法。实验包括基于视觉的顺序学习任务，使用MNIST、CIFAR-100和PASCAL 3D+数据集。

基础

先简要总结元学习、MAML以及在线学习。并在小样本学习示例中做比较，当然上述方法不仅用于小样本学习。

2.1介绍小样本学习

在少样本监督学习环境中，我们感兴趣的是一组任务，其中每个任务T都与一个概念和无穷大的输入-输出对总体相关联。目标是在与任务Ti对应的，只有少数标记的数据集下学习。小样本任务只能依赖少量标签的数据集，若想最小化损失很难。根据设置的不同，我们会按顺序或成批地接触到来自簇的许多这样的任务。通过能够利用任务的多样性，我们可能希望表现得更好，例如元学习文献中所展示的。

2.2元学习以及MAML

元学习目标是从一组任务中有效地引导，以便更快地学习新的任务。假设任务是从一个固定的分布(T~P(T))中抽取的。在元训练时，从这个分布中抽取M个任务{Ti}M i=1，并向代理提供与它们对应的数据集。在部署时，我们面临一个新的测试任务对于Tj∼P(T)，我们再次看到一个小的标记dataset Dj:= {xj, yj}。元学习算法尝试使用在M训练任务中寻找到的模型，这样当测试任务中出现Dj时，可以快速更新模型以最小化fj(w)。

MAML模型：通过学习一组初始参数实现上述目标，在测试时，在这组初始化参数基础上，通过少量几步梯度下降，就能找到目标。为了得到这组初始参数，MAML的优化问题是：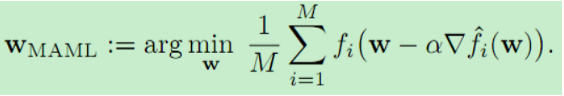

 

内梯度  从数据集D中得到。因此，MAML优化了少样本学习的泛化。注意优化问题很微妙:我们在实际目标函数中嵌入了梯度下降更新步骤。结果表明，基于梯度的方法可以与现有的自动微分库相结合，实现这一目标。由于不直接知道种群风险，因此采用随机优化技术求解式1中的优化问题。梯度调整：

 

 

元训练可以解释为学习模型参数的先验，并且微调的推理。

MAML和其他元学习算法(参见第7节)不直接适用于顺序设置，原因有两个。首先，它们有两个不同的阶段:元培训和元测试或部署。我们希望算法能以一种持续学习的方式工作。其次，元学习方法通常假设任务来自于某个固定的分布，而我们希望方法适用于非平稳的任务分布

2.3在线学习

在在线学习设置中，agent面临一系列损失函数{ft} t=1，每轮t中有一个。这些函数不需要从固定的分布中抽取，甚至可以随着时间的推移反向选择。学习者的目标是顺序决定模型参数{wt} t=1，在损失序列上表现良好。特别地，标准目标是将遗憾的概念最小化，遗憾定义为学习者的损失(PT t=1 ft(wt))与一些方法(comparator类)所能达到的最佳性能之间的差异。后悔最标准的概念是事后将其与最佳固定模型的累积损失进行比较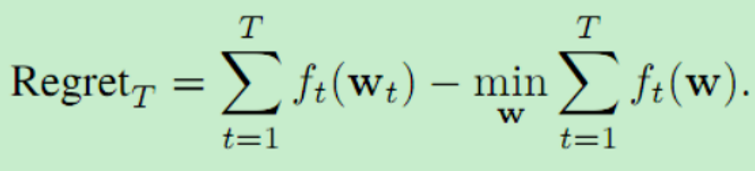在线学习的目标是设计一种算法，使这种遗憾随着T增长得尽可能慢。特别是，后悔在T中呈次线性增长的agent(算法)是非平凡的学习和适应。该设置中最简单的算法之一是follow the leader (FTL) (Hannan, 1957)，它将参数更新为：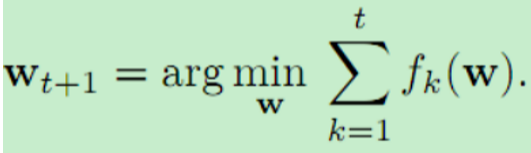

根据损失函数的性质，FTL具有强大的性能保证，一些变体使用额外的正则化来提高稳定性(Shalev-Shwartz, 2012)。对于少样本监督学习的例子，FTL将之前任务流中的所有数据合并到一个大数据集中，并将一个模型放入这个数据集中，正如第1节所提到的。正如我们在第6节的经验评估中所发现的，这种联合训练方法可能无法学习有效的模型。为了克服这个问题，我们可能需要一个比较器类的更自适应的概念，以及对这种比较器后悔程度较低的算法，我们将在下一节中讨论。

3.在线元学习的设置

我们考虑一个通用的顺序设置，其中一个agent面临一个接一个的任务。每个任务对应一轮，用t表示。目标是确定在该轮任务中表现良好的模型参数wt。w由f监控，通过最小化f来得到w。至关重要的是，我们考虑这样一种设置，在每轮部署和评估模型之前，代理可以对模型执行一些特定于本地任务的更新（perform some local task-specific updates）。这是通过一个更新过程来实现的，每轮t都是一个映射Ut：输入w，输出w'，w'在ft上表现更好。其中一种Ut是梯度下降法。（这里就是用梯度下降法优化参数的意思，妈的说的这么绕这么学术）在每轮t使用梯度下降法更新参数。（文章把损失说成后悔）

 

表示每一时刻的模型参数。后悔表示为：

 

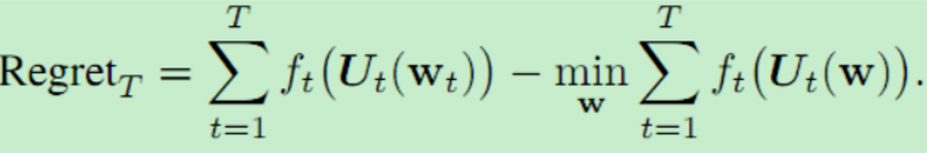
注意，我们允许比较器在当地适应手头的每一项任务;因此，比较器严格来说比学习代理具有更多的功能，因为它以批处理模式呈现所有的任务功能。在这里，再一次，实现次线性后悔表明，随着时间的推移，agent在不断改进，并且事后看来，它与最好的元学习者具有竞争力。正如前面所讨论的，在批处理设置中，当面对多个任务时，元学习的性能明显优于针对所有任务训练一个模型。因此，我们可能希望顺序学习，但事后仍能与最好的元学习者竞争，为持续学习提供一个重大飞跃。

4，算法与分析

本章概述FTML算法并简单分析其行为性能。

4.1继承自Meta Leader算法

文章提出了更新策略为：

如果学习过程在第t轮停止，这可以解释为后知后觉的代理扮演最好的元学习者。在本节的其余部分中，我们将展示在损失的标准假设下，以及在更高阶平滑度的一个额外假设下，该算法具有很强的后悔保证。在实践中，我们可能无法完全逼近fk(·)，比如当它是人口风险时，我们只有有限大小的数据集。在这种情况下，我们将利用随机逼近算法来求解Eq中的优化问题。

4.2假设

我们做出以下假设学习问题中的每一个损失函数为所有t。让θ和φ表示两个任意的选择模型参数。

平滑性假设

强凸性假设

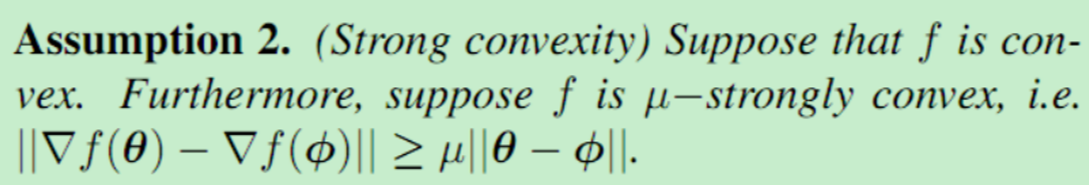
这些假设成立的例子包括有界域上的逻辑回归和L2回归。假设1.3是关于非凸分析中常见的函数高阶光滑性的表述。在我们的设置中，它允许我们描述类MAML函数的景观，其中包含一个梯度更新步骤。重要的是，这些假设并不轻视元学习设置。即使在f(·)为二次函数，对应于最简单的强凸设置的情况下，元学习和联合训练的性能也有明显的差异。有关示例说明，请参见附录A。

4.3分析

我们分析了更新过程是“梯度下降的一个单一步骤“时的FTML算法，如MAML的公式。具体来说，我们考虑的更新过程是

 

对于这个更新规则，我们首先声明下面的主要定理。

定理1：f'函数评估后一步梯度更新过程,f'是平滑非凸函数。给出了证明

有以下推论：

推论1 MAML的优化目标继承了凸函数特性：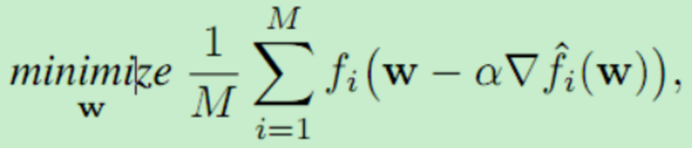

 

由于目标函数是凸的，我们可能期望一阶优化方法是有效的，因为梯度可以用标准的自动差值库有效地计算(正如Finn等人(2017)所讨论的)。事实上，这项工作提供了第一组结果(在任何假设下)，在这些结果下，类maml目标函数可以被证明和有效地优化。

我们主要定理的另一个直接推论是，FTML现在与FTL在可比较的设置(具有强凸损耗)中享有相同的遗憾保证(至多是常数因子)。

推论二：FTML继承了后悔边界：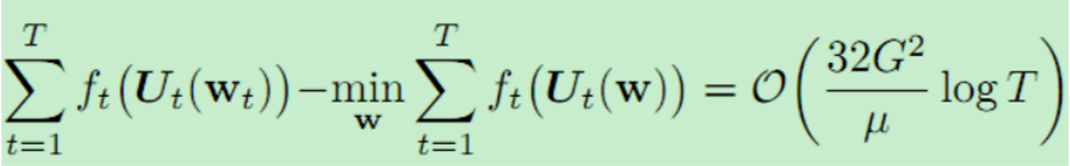

更一般地说，我们的主定理表明，基于f(·)继承的光滑性和强凸性，存在大量的在线元学习算法满足亚线性regret。多篇研究针对算法模板推导出基于子线性regret的算法。

 

5 实用的在线元学习算法

实际应用中许多问题是非凸的，而梯度下降法以及AdaGrad在非凸情况可以表现良好。从这些成功中获得灵感，我们在本节中描述了FTML的一个实际实例，并在第6节中对其性能进行了经验评估。

将FTML算法应用于具有高容量神经网络模型的小样本监督学习时，主要考虑的问题是：(a)式(4)中的优化问题没有封闭形式解，(b)我们没有访问总体风险ft，只能访问数据的子集。为了克服这两个限制，我们可以使用迭代随机优化算法。具体来说，通过采用MAML算法(Finn et al.， 2017)，我们可以使用一个小批量Dtrk作为更新规则的随机梯度下降，以及一个独立采样的小批量Dval k作为随机梯度下降来优化参数。梯度计算如下：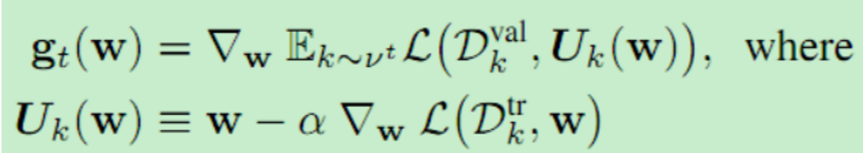

vt表示样本的分布，L(D,W)是损失函数。使用独立取样的小批量Dtr和Dval最小化了内部梯度更新Ut与外部优化之间的交互作用(式4)。损失采用了Adam。公式中的Uk只是用了一部梯度更新。我们观察到在内循环中采用多个梯度步骤是有益的。

现在我们已经导出了梯度，整个算法的过程如下：我们首先初始化一个任务缓冲区B=【】，当在第t轮出现一个新任务时，我们将任务Tt添加到B中，并初始化一个特定于任务的数据集Dt =[]，当任务Tt的数据增量到达时，该数据集被附加到后面。当任务Tt的新数据到达时，我们迭代地计算并应用Eq. 5中的梯度，它使用了迄今为止看到的所有任务的数据。一旦所有的数据(有限大小)都到达Tt，我们将继续任务Tt+1。算法1进一步描述了这个过程，包括我们接下来讨论的求值。

为了评估模型在特定轮t内的任何点的性能，我们首先使用迄今为止在轮t内看到的所有数据(Dt)更新模型，这在算法2的Update-Procedure子例程中进行了概述，注意，这与元优化中使用的updateUt不同。

它使用固定大小的小批处理，因为多样本元学习在计算上很昂贵，而且需要大量内存。在实践中，我们使用最多25个大小的更新小批进行元培训，而评估可能对某些任务使用数百个数据点。在模型更新后，我们使用任务Tt中的helout数据Dtest t来度量性能。这些数据不会在任何时候向在线元学习者公开。进一步,我们也评估工作学习效率,这对应于Dt的大小需要达到特定的性能阈值γ,如γ= 90%分类精度或γ值对应于一定的损失。如果达到阈值的数据足够少，那么从以前的任务中学习到的先验知识是有用的，我们已经实现了正迁移。

6 实验评估

我们的实验评估研究了实际的FTML算法(第5节)在几个基于视觉的学习任务的背景下。这些任务包括MNIST数据集的合成修改，基于PASCAL3D+模型的合成图像位姿检测(Xiang et al.， 2014)，以及CIFAR-100数据集的逼真的在线图像分类实验。我们实验评估的目的是研究以下问题:(1)在线元学习(尤其是FTML)能否成功应用于多个非平稳学习问题?和(2)在线元学习(FTML)提供经验的好处超过之前的方法?

为此，我们比较了以下算法:(a)对所有数据进行训练(TOE)对目前所有可用数据进行训练(包括t轮Dt)，并训练单个预测模型。这个模型是直接测试，没有任何具体的适应，因为它已经训练了Dt。(b)从零开始训练，随机初始化wt, finetunes使用Dt。

(c)微调联合训练，在第t轮联合训练所有数据，直到第1轮，然后只使用Dt对其进行微调，专门对第t轮进行微调。这与使用FTL的标准在线学习方法相对应(没有任何元学习目标)，然后进行特定于任务的微调。

我们注意到，TOE是一个非常强的比较点，能够跨任务重用表示，这在之前的一些持续学习著作(Rusu et al.， 2016;Aljundi等，2017;王等，2017)。然而，与FTML不同的是，TOE不会显式地跨任务学习结构。因此,它可能无法充分利用的信息数据,并将可能无法进一步学习新任务只有几个例子,该模型可能产生负迁移,如果新任务大大不同于以前见过的,之前一直在观察工作(Parisotto et al ., 2016)。从头开始独立地培训每个任务可以避免负迁移，但也可以防止任务之间的重用。当给定任务的数据量很大时，我们可能期望从零开始的训练能够很好地执行，因为它可以避免负迁移，并且可以针对特定的任务进行专门的学习。最后，带有微调的FTL代表了一种自然的在线学习比较，它原则上应该结合从头开始学习和从头开始学习的最佳部分，因为这种方法特别适合于每个任务，并从以前的数据中获益。然而，与FTML相比，这种方法没有明确的元学习，因此可能不能充分利用任务中的任何结构。

6.1. Rainbow MNIST

在这个实验中，我们基于MNIST字符识别数据集创建了一系列的任务。我们通过多种方式转换数字来创建不同的任务，例如7种不同颜色的背景，2种比例(一半大小和原始大小)，以及4种90度间隔的旋转。如图2所示，一项任务包括使用随机采样的背景、比例和旋转对数字进行正确分类。总共有56个任务。我们将MNIST训练数据集划分为56批样本，每批样本包含900幅图像，并对每批图像应用相应的任务转换。任务的排序是随机选择的，我们将90%的分类准确率作为熟练度阈值。

图3中的学习曲线显示，随着每个新任务的添加，FTML学习任务的速度越来越快。我们还观察到，FTML在效率和最终性能上显著优于其他方法。FTL的性能优于TOE，因为它执行特定于任务的适应性，但它的性能仍然低于FTML。我们假设，虽然先前的方法在学习过程中随着看到更多的任务而提高效率，但它们很难防止每个新任务的负迁移。我们最后的观察是，与包含来自其他任务的数据的模型相比，训练独立的模型并不能有效地学习;但是，它们最终的性能与900个数据点相似。

6.2. Five-Way CIFAR-100

在本实验中，我们建立了一个基于CIFAR-100数据集的5路分类任务序列，其中包含了比MNIST更具挑战性和真实感的RGB图像。每个分类问题都涉及到CIFAR-100中的100个类中的一个新引入的类。因此，不同的任务对应于不同的标签空间。任务的排序是随机选择的，我们使用分类精度来衡量性能。由于不太清楚这个任务的熟练程度阈值应该是多少，所以我们在看到不同数量的数据点之后评估每个任务的准确性。由于这些任务是相互排斥的(随着标签空间的变化)，为每个任务使用不同的最终层来训练TOE模型是有意义的。与此极其相似的方法是使用元学习方法，但是只允许最后的层参数适应每个任务。此外，这种元学习方法与我们的完整FTML方法相比更加直接，这种比较可以让我们了解在线元学习是简单地学习特性并在最后一层执行培训，还是将这些特性适应于每个任务。因此，我们将这最后一层在线元学习方法与多头TOE学习方法进行了比较。结果(参见图4)表明，与独立模型和具有共享特征空间的模型相比，FTML学习效率更高。右边的结果表明，从零开始的训练在2000个数据点上取得了良好的性能，达到了与FTML类似的性能。然而，FTML的最后一层变体似乎没有能力在所有任务上达到良好的性能。（看不懂图片）

6.3. Sequential Object Pose Prediction（序列目标位姿检测）

在最后的实验中，我们研究了一个三维姿态预测问题。每一项任务都包括学习预测图像中物体的整体位置和方向。我们构造一个数据集的合成图像使用50对象模型从9中不同的对象类PASCAL3D +数据集(湘et al ., 2014),呈现对象放在桌上使用任- der陪同MuJoCo物理引擎(托多罗夫et al ., 2012)(见图2)。将一个对象在ta - ble,我们选择一个随机二维位置,以及一个随机的方位角度。每个任务对应一个随机采样的摄像机角度不同的对象。

我们在表的一角放置一个红点，以提供该位置的全局参考点。使用这个设置，我们构造了90个任务(平均每个对象大约有2个摄像机视点)，每个任务有1000个数据点。所有的模型都经过训练，回归到全局2D位置和方位角(沿z轴旋转的角度)的正弦和余弦值。对于损失函数，我们使用均值平方误差，并将熟练度阈值设置为0.05。我们在图5中显示了这个实验的结果。研究结果表明，元学习能够在学习过程中提高新任务的效率和性能，解决了许多只有10个数据点的任务。与之前的设置不同，TOE的性能远远优于从零开始的训练，这表明它可以有效地利用来自其他任务的先前数据，这可能是因为姿态检测任务之间的结构相似性更大。然而，FTML的性能表明，通过显式优化快速有效地学习新任务的能力，可以实现更好的传输。最后，我们发现FTL的性能与TOE相当，甚至更差，这表明当模型没有被显式地训练为能够有效地进行微调时，特定于任务的微调可能导致过度拟合。

7. Connections to Related Work

我们的工作建议使用元学习或学习学习(Thrun &普特,1998;Schmidhuber, 1987;奈克,玛蒙，1992)，在网上(基于遗憾的)学习的背景下。我们在第2节中回顾了这些方法的基础，并总结了其他相关的工作。

元学习:以前的元学习工作已经提出了学习一个更新规则或优化器来快速适应(

(Hochreiter et al., 2001; Bengio et al., 1992; Andrychowicz et al., 2016; Li & Malik, 2017; Ravi & Larochelle, 2017)通过一个模型输出另一个模型的权重((Ha et al., 2017)，而其他研究使用了通过直接摄取数据集来学习的循环模型(San-toro et al., 2016; Duan et al., 2016; Wang et al., 2016;

Munkhdalai & Yu, 2017; Mishra et al., 2017)。而一些元学习作品则考虑了元测试时的在线学习设置(Santoro et al., 2016; Al-Shedivatet al., 2017; Nagabandi et al., 2018），几乎所有以前的元学习算法都假设元训练任务来自一个平稳分布。此外，大多数先前的工作并没有评估元学习算法的版本，当呈现连续的任务流时。最近的工作考虑使用Dirichlet过程混合模型处理元学习参数上的非平稳任务干扰(Grant et al., 2019)。与之前的工作不同，我们在MAML算法上引入了一个简单的扩展，没有参数混合，并提供了理论保证。

持续学习:我们的问题设置与持续学习或终身学习相关(但不同于)(

(Thrun, 1998;Zhao & Schmidhuber, 1996)。在终身学习中，最近的一些论文都着重于避免遗忘和负向后迁移(Goodfellow et al., 2013; Kirk-patrick et al., 2017; Zenke et al., 2017; Rebuffi et al., 2017;Shin et al., 2017; Shmelkov et al., 2017; Lopez-Paz et al.,2017; Nguyen et al., 2017)。其他一些论文则侧重于在添加新任务时保持合理的模型容量(Lee et al., 2017; Mallya & Lazebnik, 2017)。在本文中，我们通过维护所有观测数据的缓冲区来避免灾难性遗忘问题(Isele &Cosgun, 2018)。在未来的工作中，我们希望了解有限的内存和灾难性遗忘之间的相互作用的变种FTML算法。在这里，我们转而关注正向转移的问题——在非平稳学习环境中最大化学习新任务的效率。以前的工作也考虑过将跨任务的联合训练与特定于任务的适应相结合的设置((Barto et al., 1995; Lowrey et al., 2019)，但没有明确使用元学习。此外，不同于以往的作品(Ruvolo & Eaton, 2013; Rusu et al., 2016; Aljundi et al., 2017; Wang et al., 2017)我们还关注有几十个或数百个任务的设置。这个设置很有趣，因为可以从以前的任务转移更多的信息，而且我们可以使用更复杂的技术，例如元学习来进行转移，使代理在经历大量任务之后能够转向少镜头学习。

在线学习:与持续学习类似，在线学习处理的是连续设置的流任务。众所周知，在网上学习中，FTL有很好的后悔保证，但往往是计算昂贵的。因此，在开发计算上更便宜的算法(Cesa-Bianchi & Lugosi, 2006; Hazan et al., 2006; Zinkevich, 2003; Shalev-Shwartz, 2012)。同样，在这项工作中，我们避开计算方面的考虑，首先研究FTL的元学习模拟是否能够提供性能增益。为此，我们推导了FTML算法，它与功能强大的自适应比较器类进行任务特定的自适应相比，后悔率较低。我们将设计计算效率更高的FTML版本留给未来的工作。

为了避免后见之即知的单一最佳模型所带来的陷阱，在线学习文献也研究了后悔的三个具体概念，其中最接近的设置是动态后悔和自适应后悔或跟踪后悔。在动态后悔设置中(Herbster &Warmuth, 1995; Yang et al.,2016; Besbes et al., 2015），将在线学习者模型序列的性能与序列中每个损失函数对应的最优解序列进行比较。不幸的是，下界(Yang et al.，2016)表明比较器类过于强大，在一般情况下可能无法提供任何非琐碎的学习。为了克服这些限制，先前的工作对损失函数或组件模型的更改速度进行了限制(Hazan &Comandur, 2009;Hall& Willett,2015;herbst,Warmuth, 1995)。相比之下，我们考虑了一个不同的自适应后悔的概念，即学习者和比较者都可以使用更新过程。更新过程允许比较器为不同的损失函数提供不同的模型，从而作为一个功能强大的比较器类(事后对比固定模型)。对于这个设置，我们推导出了次线性后悔算法，没有对损失函数的序列施加任何限制。我们相信，这个设置捕捉了持续终生学习的精神和实践，并带来了有希望的实证结果。

8. Discussion and Future Work

在本文中，我们引入了在线元学习问题陈述，旨在将元学习和在线学习领域联系起来。在线元学习在某种意义上为理想的现实学习过程提供了一个更自然的视角：一个与不断变化的环境交互的智能代理应该利用流体验来掌握手头的任务，并在未来更加熟练地学习新的任务。对提出的FTML算法进行了分析，结果表明该算法达到了对数后悔。然后，我们演示了如何将FTML应用于实际算法。实验结果表明，提出的算法性能优于已有的算法。在本节的其余部分中，我们将重申在线元学习设置的一些显著特性(第3节)，并概述未来工作的途径。

更强大的更新过程。在这项工作中，我们集中分析的情况下，更新程序Ut，由MAML的启发，对应于梯度下降的一个步骤。然而，在实践中，许多使用MAML的工作(包括我们的实验评估)在更新过程中使用多个梯度步骤，并通过这些多个梯度步骤所采取的整个路径进行反向传播。分析这种情况，以及潜在的更高顺序的更新规则，也将使未来的工作更加令人兴奋。

内存和计算限制。在这项工作中，我们的主要目的是了解是否可以在顺序设置中进行元学习。为此，我们提出了基于FTML模板的在线学习算法。正如第7节所讨论的，众所周知，FTL具有较差的计算性能，因为随着新的损失函数的累积，FTL的计算成本会随着时间增长。此外，在许多实际的在线学习问题中，存储以前任务的所有数据点是具有挑战性的(有时是不可能的)。虽然我们展示了我们的方法可以有效地按顺序学习近100个任务，而不需要大量的计算或内存负担，但是可伸缩性仍然是一个问题。像镜像下降这样不存储所有过去经验的流化算法也能成功吗?我们的主要理论结果(第4.3节)表明，存在大量在线元学习算法享受次线性遗憾。利用在线学习的大量工作，特别是镜像下降，来开发计算上更便宜的算法，将使未来的工作令人兴奋。

 

好好研究本文的参考文献！！！参考相关工作