动态规划(DP)初步

一、定义：

百度百科是这样说的：

在计算机中：

DP是通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。（这些定义看不懂没关系，下面通过引例来介绍）

二、引例：最长公共子序列（LCS）

1、题目描述：

        给定俩个字符串序列X,Y。X的长度为m,Y的长度为n,求其最长公共子序列。

        例如：X:ABCBDAB

                  Y:BDCABA

 则LCS（X,Y）={BCBA，BCAB，BDAB ，BDBA}

 注：1.像‘A’，‘C’这样的不是LCS(X,Y)，当X,Y只有一个字母相同时。

        2.LCS不止一个

3.LCS(X,Y)只是一种关系，并非函数，表示LCS中的某一个，当然，这里表述也不是太标准，我们知道就行。随意点还是挺不错的。

2、做题准备：

        在分析问题之前，我们先来看几个概念：

     （1）子序列：

                子序列是有序的，但不一定是连续，作用对象是序列。

                例如：序列 X = <B, C, D, B> 是序列 Y = <A, B, C, B, D, A, B> 的子序列，

                          对应的下标序列为 <2, 3, 5, 7>。

     （2）子串：

                子串是有序且连续的，左右对象是字符串。
　　         例如 a = abcd 是 c = aaabcdddd 的一个子串，但是 b = acdddd 就不是 c 的子串。

3、分析问题：

        在知道上面俩个概念后，我们就可以开始做题了。

        1）穷举法

        看到这个问题，我们的首先就想到了“穷举法”，这也是我们肉眼观察的方法。即：先穷举出X[1...m]的所有子序列，再在Y[1...n]序列中找是否存在这个子串，如果存在，记录下来，在比较长度，选择最长的序列。即为X,Y的LCS。

接下来我们分析下T（n）：

       我们找到了一个X[1...m]的子串，判断是否存在Y中，我们只需扫一遍Y就可以了，故为O（n）。

       那么X[1...m]有多少子串呢？答案是2^m。为什么呢？我们可以这样想，X中每个字符都有俩种可能，在子串和不在子串，总共有m个字符，故时间复杂度为O（2^m）。（此中为最坏情况，即每个子串都不相同）

        故T（n）=O(n*2^m)。时间复杂度为指数级，太慢！那么有什么可以改进呢？

2）改进算法

            先来看下面几个问题：

            1.LCS(X,Y)的长度？（是固定的！）

            2.如何来拓展找到它自己的LCS。（我们只需找到这些长度的X子串，来比较Y中是否存在）

            这样，我们就简化成了数值问题。

            我们定义C[i,j]=| LCS（X[1...i],Y[1...j) |   (这里我们用| S |来表示序列S的长度）

            这样，我们题目中的| LCS[X,Y] |=C[m,n]。

            那么如何求C[i,j]呢？我们有如下公式：

             

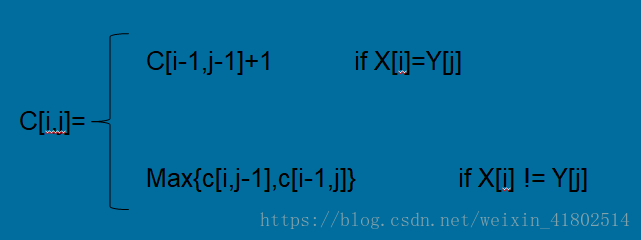
例如：1）输入子序列 <AGGTAB> 和 <GXTXAYB>。最后一个字符匹配的字符串。这样的 LCS 的长度可以写成：

       L(<AGGTAB>, <GXTXAYB>) = 1 + L(<AGGTA>, <GXTXAY>)

　　    2）输入字符串“ABCDGH”和“AEDFHR。最后字符不为字符串相匹配。这样的LCS的长度可以写成：

       L(<ABCDGH>, <AEDFHR>) = MAX ( L(<ABCDG>, <AEDFHR>), L(<ABCDGH>, <AEDFH>) )

下面我们来证明这个公式：

1.if X[i]=Y[j]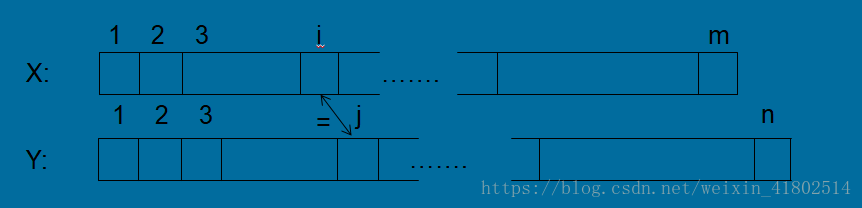             

        令Z[1...k]=LCS(X[1...i],Y[1...j])，那么Z[k]=X[i]=Y[j]。

        我们可以这样想：如果X，Y中没有X[i],Y[j]，其余都一样，那么这俩个新的X,Y的LCS加上1不就是X，Y的LCS。

        我们不难发现，这俩个新的X,Y的LCS=(X[1...i-1],Y[1...j-1]),则LCS（X,Y）=LCS（X[1...i-1],Y[1...j-1]）+1我们也可以说：Z[1...k-1]=LCS(X[1...i-1],Y[1...j-1])。下面我们用经典的反证法来证明。

        假设：w是个更长的CS（公共子序列），则| W | > K-1。

        我们在w的最后加上Z[K],所以X[1...i]和Y[1...j]的一个子序列长度  > k ,与| LCS（X,Y）| 矛盾，假设不成立，得证。

        所以，我们就可以用这个公式递归下去求LCS（X,Y）。

       说到这，我们就引出了DP的第一个特征：

       最优子结构：问题（计算机中的问题，如排序）的一个最优解包含了子问题的最优解

        如： if Z=LCS(X,Y)

                 Z的任何前缀 都是 X的某个前缀和Y的某个前缀的LCS

2.if      X[i] != Y[j]

       那么就等于C[i-1,j](X序列去掉第i个和Y的LCS长度）和C[i,j-1]（Y序列去掉第j个和X的LCS的长度）的最大值，这个可以很直观的看出，此处就不证明了。

下面我们就可以 计算LCS了。

给出伪码描述：

int LCS(x,y,i,j)
{
    if(x[i] == y[j]){
        c[i][j]=c[i-1][j-1]+1;
    }else{
        c[i][j]=max(c[i-1,j],c[i,j-1]);
    }
    return c[i][j];
}

        我们来考虑下最坏的情况：总是X[i] != Y[j]。

         这里给出递归树，看看是如何求解C[i][j]的:

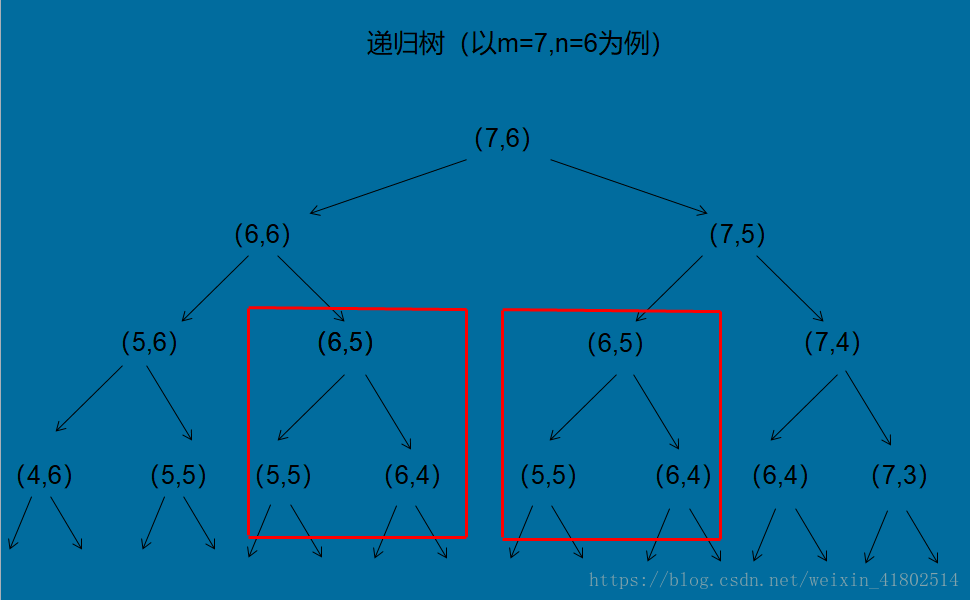
        这颗树的高度为m+n，所以计算量是m+n的指数级，还是太慢！为什么呢？

        我们发现上面的递归树有着重复计算！（如图中红色部分）

       此时，就引出了DP的第二个特征：  

       重叠子问题：一个递归过程包含少数独立的子问题被重复计算了多次。

       回到这个问题，那么这个问题的独立子问题为n*m个。

       此时我们可以用用一个二维数组来标记这个地方是否计算过。

       下面给出伪码描述：

int LCS(x,y,i,j)
{
    //如果c[i][j]没有计算过
    if(c[i][j]==NULL){
        if(x[i] == y[j]){
            c[i][j]=c[i-1][j-1]+1;
        }else{
            c[i][j]=max(c[i-1,j],c[i,j-1]);
        }
    }
    return c[i][j];
}

        我们再来分析下这个算法的时间和空间复杂度：

        T(n) = O(m*n)

        我们可以采用“均摊”这种思想来思考：

易知计算出每个C[i][j]所需的时间为常数级，打个比方，得到一个C[i][j]需要支付d元，如果需要递归，计算之前的C[i][j],所需花费也是之前支付，在此时只需支付d元。共n*m个需要计算，所以时间复杂度为O（m*n）。

S（n）=O（n*m）

因为我们开辟了c[][]，以及开辟一个和c等大数组来记录c中某个值是否计算过。

以上算法是自顶向下，而真.DP是自底向上。

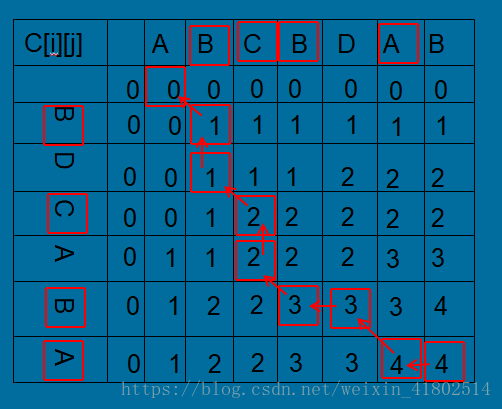
从而我们有了以下表格C[i][j]:

上面一开始初始化为0，计算法则为上述公式，在这里可以描述为：

X[i] != Y[j]时，C[i][j]=max{C[i-1][j],C[i][j-1]}

X[i] == Y[j]时，C[i][j]=C[i-1][j-1]+1

此时时间复杂度没变，可是空间复杂度可以降低！

S(n)=O(min{m,n})    为什么？

我们可以发现，求第i行C[i][]时，只需要第i-1行。如计算第三行时，只需要知道第二行就可以了，第一行知不知道无所谓。

为了节省空间，我们可以选择min{m,n}，即可以一行一行解决，也可以一列一列解决（看哪个小，就选择哪个）

知道了这些，我们可以采用“回溯法”求得LCS（X,Y）。

4.实现代码：

#include<cstdio>
#include<string>
using namespace std;

const int maxn = 100;
char x[maxn], y[maxn];
int dp[maxn][maxn], path[maxn][maxn];
//dp[][]就是c[][],path保存路径指向，以方便打印公共子序列

int Lcs(char x[], char y[])
{
    int i,j,lenx = strlen(x+1),leny = strlen(y+1);
    memset(dp,0,sizeof(dp));//初始化
    for(i = 1; i <= lenx; ++i)
        for(j = 1; j <= leny; ++j){
            if(x[i] == y[j])
                dp[i][j] = dp[i - 1][j - 1] + 1, path[i][j] = 1;
            else if(dp[i - 1][j] >= dp[i][j - 1]) //x[i] != y[j]时，为了记录路径，所以采用了这种写法
                dp[i][j] = dp[i - 1][j], path[i][j] = 2;
            else
                dp[i][j] = dp[i][j - 1], path[i][j] = 3;
        }
    return dp[lenx][leny];
}//求序列x和y的LCS
void PrintLcs(int i, int j)
{
    if(i == 0 || j == 0) return;
    if(path[i][j] == 1){
        PrintLcs(i - 1, j - 1);
        putchar(x[i]);
    }//当path[]=1时，为相同子序列中的，输出
    else if(path[i][j] == 2)
            PrintLcs(i - 1, j);
    else PrintLcs(i, j - 1);//其余俩种情况，只需返回，无需打印
}//打印LCS

int main()
{
    while(1){
        scanf("%s",x+1);
        scanf("%s",y+1);
        printf("%d\n", Lcs(x,y));
        PrintLcs(strlen(x+1), strlen(y+1));
        printf("\n");
    }
    return 0;
}

三.一些经典DP模型

1.最长××子序列

    最长 递增/ 递减/ 非递增/ 非递减子序列，这四个是一种模型。

    以最长递增子序列为例：

    如：13  7  9  16  38  24  37  18

    我们设dp[i]表示以num[i]结尾的最长递增子序列长度。

    初始化：dp[i]=1  for  1<=i<=n

    状态转移方程：dp[i] = max(dp[j]) + 1 when num[j] < num[i] for 1<=j＜i

    (注：这四种情况，状态方程都一样，只是使用状态转移方程的条件不一样。

            递减：num[j] > num[i]

            非递减：num[j] <= num[i]

            非递增：num[j] >= num[i])

    T(n)=O(n^2)

    实现代码：

#include<cstdio>
#include<iostream>
using namespace std;

const int maxn = 100;
int dp[maxn],x[maxn];
int k;

void getdp(){
    dp[1]=1;
    for(int i = 2;i <= k;++i){
        dp[i]=1;
        for(int j = 1;j < i;++j){
            if(x[j] < x[i]){
                dp[i] = dp[i] > dp[j]+1 ? dp[i] : dp[j]+1; 
            }//若改为求其它子序列，只需改if中的条件就可以 
        }
    }
}
//获得dp数组的值

int main()
{
    while(scanf("%d",&k) != EOF){
        for(int i = 1;i <= k;++i){
            scanf("%d",&x[i]);
        }
        getdp();
        int len=dp[1];
        for(int i = 1;i <= k;++i){
            if(dp[i] > len){
                len = dp[i];
            }
        }
        printf("%d\n",len);
    }
    return 0;
}

   从这类问题拓展出来的问题有 瓶子序列，合唱队形（九度oj1131）等。

    还有一种类型就是我们的引例，最长公共子序列。

2.背包问题：

点击打开链接    这是一位大牛写的背包九讲

    在这里只介绍0/1背包：

    有N种物品（每种物品1件）和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。

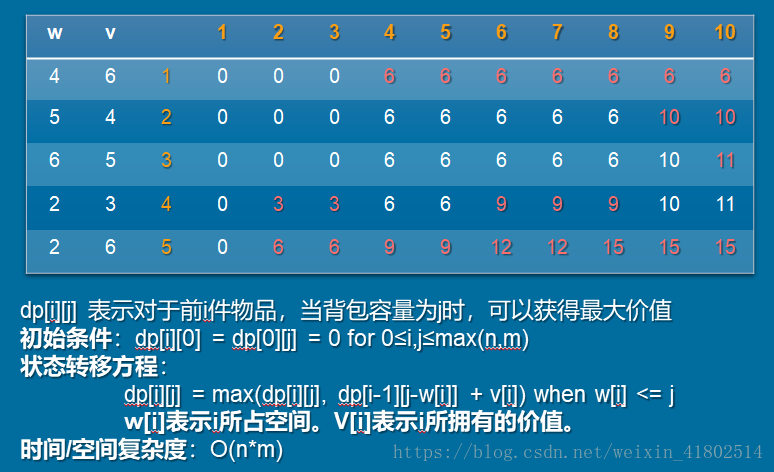
        状态转移方程所代表的意思是：如果第i件物品不放入背包，则我们用空间为j的背包来放前i-1件物品。

        如果第i件物品放入背包，我们用空间为j-w[i]的空间放i-1件物品，最大价值为dp[i-1][ j-w[i] ] + v[i]。

        其实现主要代码

for(int i = 1;i<=m;++i){
    for(int j = 1;j<=W;++j){
        dp[i][j] = dp[i-1][j];
        if(j-w[i] >=0) dp[i][j] = max(dp[i][j], dp[i-1][j-w[i]] + v[i]);
    }
}

       这里我们可以想到我们的引例中最后降低空间复杂度的做法，它其实是滚动数组

       那么，在这里怎么做呢？我们可以倒序计算(这里和引例都是计算时只需要上面一行，但此处需要的上面一行在计算数据前的所有数据，因为w[i]不定)，举个例子，计算dp[i][j],它只需要dp[i-1][x] (x < j),下面给出主要代码：

for(int i =1; i<=n;++i){
    for(int j = m; j>=w[i];--j)
        dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}

最后，可以去看看这篇博客，里面有动态规划的解题一般思路（以树塔问题为例）

点击打开链接