LeetCode 42. 接雨水(单调栈)

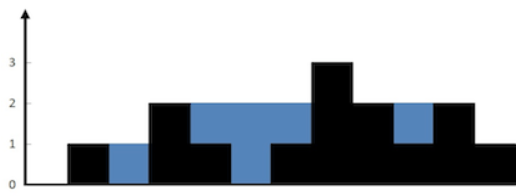
示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

 https://leetcode-cn.com/problems/trapping-rain-water】

思路: 维持一个递减的单调栈,当要压入栈的位置的高度h[b]大于栈顶元素的高度h[a]时,栈顶元素a弹出,并计算a和b之间存水量,
    -由于h[a] < h[b] 因此存水量的高度由h[a]决定,且还需要保存h[a]到last变量中,因为在位置a的左边还可能由c,c满足h[c] > h[a]
    -且 h[c] < h[b],这样在计算c和b之间的存水量时,就不能再包含a和b之间的存水量了

注意: 题目给出的图很好,很能说明这道题的解法,好好看下这张图

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> stk;
        int sum = 0,last;
        for (int i = 0; i < height.size(); ++i){
            last = 0;                             // 每次last要清空,这里要理解last的作用就知道为什么last要每次清空了
            while(stk.size() && height[stk.top()] <= height[i]){
                sum = sum + (i - stk.top() - 1) * (height[stk.top()] - last);  // height[stk.top()] - last 
                last = height[stk.top()];
                stk.pop();
            }
            if (stk.size())   // 如果左边有更高的位置x,那么h[i]就和h[x]也可以存水,因此还需要再计算一次
                sum += (i - stk.top() - 1)*(height[i] - last);           
            stk.push(i);
        }
        return sum;
    }
};