python——Dijkstra最短路径（以一组具体的数据为例，也可以输入一组数据。有向图）

最新推荐文章于 2024-08-13 20:47:36 发布

原创

最新推荐文章于 2024-08-13 20:47:36 发布 · 2.2k 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#dijkstra最短路径 #python求最短路径 #Dijkstra算法 #Dijkstra实现有向图的最短路径求取 #dijkstra有向图

本文介绍了Dijkstra最短路径算法的基本原理，并通过一个具体实例解释算法的应用。使用Python编写了求解有向图最短路径的代码，探讨了代码的运行效果和存在的优化空间，包括处理大规模数据时的改进方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、Dijkstra

基本原理：

按照最短路径递增的次序，逐次搜索出从起点到网络中其余所有点的最短路径。

给出从一条起点到终点的初始路径；
对这条路径不断的优化，使其距离减小；
当不能再被优化时，即为最短路径。

基本思想：设置一个集合S存放已经找到最短路径的顶点，S的初始状态只包含源点v，对vi∈V-S，假设从源点v到vi的有向边为最短路径。以后每求得一条最短路径v, …, vk，就将vk加入集合S中，并将路径v, …, vk , vi与原来的假设相比较，取路径长度较小者为最短路径。重复上述过程，直到集合V中全部顶点加入到集合S中。

二、以一个实例来助于理解

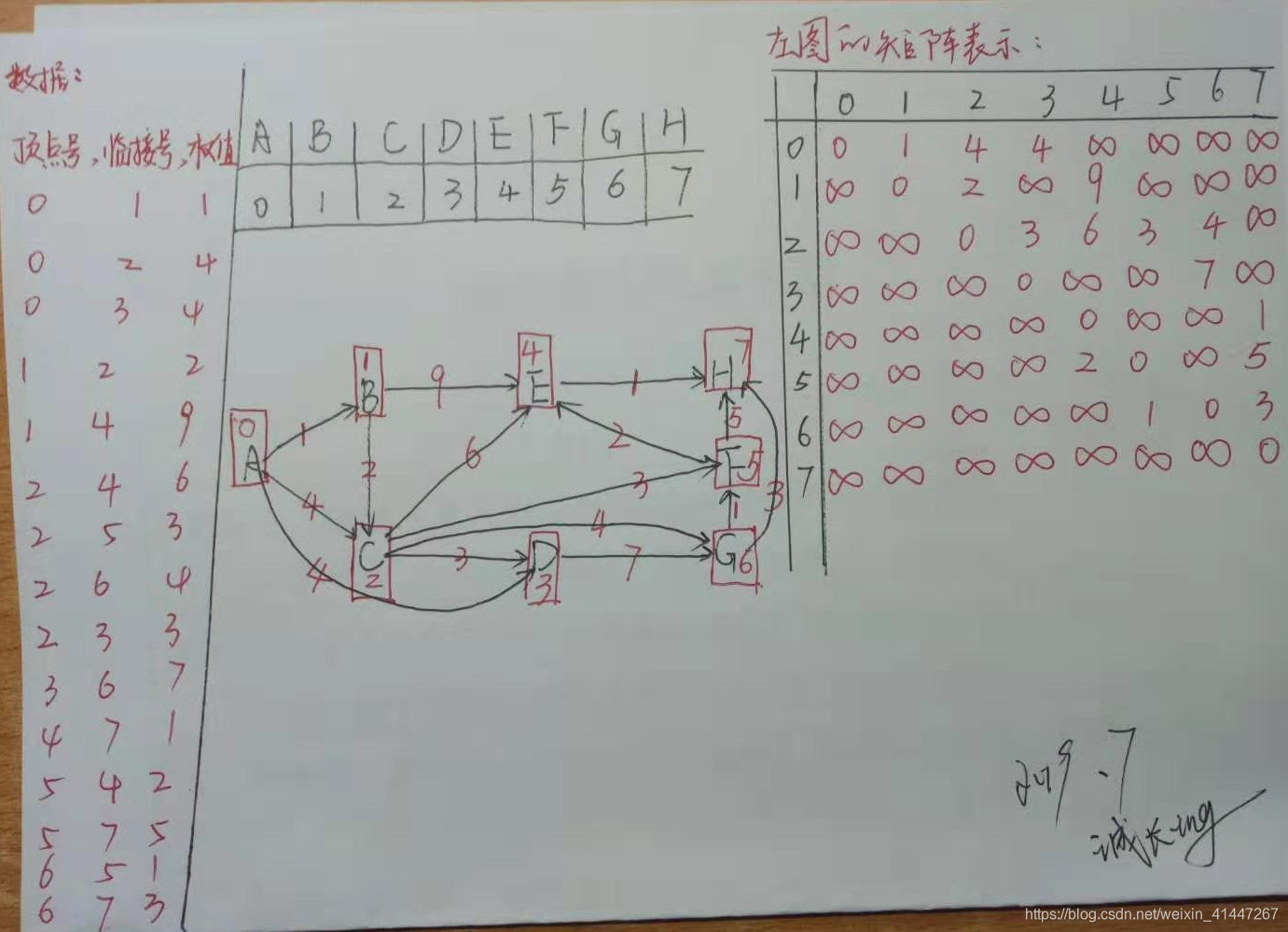
如图是有向图，我们根据有的数据（顶点号，临接号，权值）画出有向图，然后根据有向图写出图的矩阵表示。

其中A,B,C,D,F,G,H分别用0,1,2,3,4,5,6,7表示。

从以上数据我们可以得到数据中：图的顶点有8个，顶点之间用有向线连接的有15条线段。

三、python代码

'''
顶点 A B C D E F G H
     0 1 2 3 4 5 6 7
A—F表示顶点号，分别用数字0,1,2,3,4,5,6,7代替；
顶点号，临接号，权值
0,1,1
0,2,4
0,3,4
1,2,2
1,4,9
2,4,6
2,5,3
2,6,4
2,3,3
3,6,7
4,7,1
5,4,2
5,7,5
6,5,1
6,7,3

'''
import sys
# 定义不可达距离
max=sys.maxsize

# points点个数，edges边个数,graph路径连通图的矩阵表示,start起点,end终点
def Dijkstra(points, edges, graph, start, end):
    map = [[max for i in rang