（读书笔记）周志华《机器学习》第4章：决策树

最新推荐文章于 2025-02-26 21:56:42 发布

原创

最新推荐文章于 2025-02-26 21:56:42 发布 · 649 阅读

0 ·

CC 4.0 BY-SA版权

决策树

本章内容概述：

基本流程：决策树是如何决策的？决策树学习的目的是什么？如何生成一颗决策树？
划分选择：怎样选择最优划分属性？有哪些判断指标？具体是怎样运作的？
剪枝处理：为什么要剪枝？如何判断剪枝后决策树模型的泛化性能是否提升？预剪枝和后剪枝是怎样工作的？有什么优缺点？
连续与缺失值：如何把连续属性离散化？如何基于离散化后的属性进行划分？和离散属性有何不同？如何在属性值缺失的情况下选择最优划分属性？给定划分属性，如何划分缺失该属性值的样本？
多变量决策树：决策树模型的分类边界的特点是怎样的？多变量决策数是如何定义的？又是如何工作的？

4.1 基本流程

决策树（decision tree）是一种模仿人类决策的学习方法。举个例子，比方说你要决策一下你今晚要做什么事情，最终经过一系列的判断做出要做什么的决策。那么使用下图就能很好地表示你的决策逻辑（即一颗决策树）。

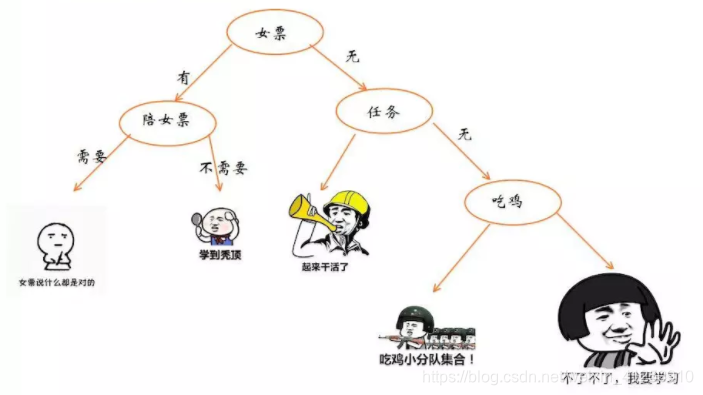
在这里插入图片描述
在上图的决策树中，决策过程的每一次判定都是对某一属性的选择，决策最终结论则对应最终的判定结果。一般一颗决策树包含：一个根节点、若干个内部节点和若干个叶子节点，易知：

每个非叶节点表示一个特征属性测试。
每个分支代表这个特征属性在某个值域上的输出。
每个叶子节点存放一个决策结果，也即分类任务中的类别标记。
每个节点包含的样本集合通过属性测试被划分到子节点中，根节点包含样本全集。

决策就是从根节点开始走到叶节点的过程。每经过一个节点的判定，数据集就按照属性值划分为若干子集，在内部节点做判定时只需要考虑对应的数据子集就可以了。

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树。

决策树生成是一个递归过程，决策树学习的基本算法：

在这里插入图片描述
决策树构造的过程中，有三种情形会导致递归返回：(1) 当前结点包含的样本全属于同一类别，这时直接将该节点标记为叶节点，并设为相应的类别；(2) 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分，这时将该节点标记为叶节点，并将其类别设为该节点所含样本最多的类别；(3) 当前结点包含的样本集合为空，不能划分，这时也将该节点标记为叶节点，并将其类别设为父节点中所含样本最多的类别。

可以看出：决策树学习的关键在于如何选择划分属性，不同的划分属性得出不同的分支结构，从而影响整颗决策树的性能。属性划分的目标是决策树的分支节点所包含的样本尽可能属于同一类别，即让各个划分出来的子节点尽可能地“纯”。因此下面便是介绍量化纯度的具体方法，决策树最常用的算法有三种：ID3，C4.5和CART。

4.2划分选择

4.2.1 信息增益

在决策树模型中，我们不断进行判定的初衷是希望划分后需要考虑的可能更少，准确地说，是希望所得子节点的纯度（purity）更高（也可以说是混乱程度更低）。著名的 ID3算法 使用信息增益为准则来选择划分属性。

信息熵(information entropy)是一种衡量样本集纯度的常用指标：

$-\sum_{k=1}^{|\mathcal{Y}|}p_klog_2p_k$

其中 $|\mathcal{Y}|$ 为类别集合， $p_k$ 为该类样本占样本总数的比例。

信息熵越大，表示样本集的混乱程度越高，纯度越低。

信息增益（information gain）定义如下：

$\sum_{v=1}^{V}\frac{|D^v|}{|D|}Ent(D^v)$

描述的是按某种属性划分后纯度的提升，信息增益越大，代表用属性 $a$ 进行划分所获得的纯度提升越大。其中 $V$ 表示属性 $a$ 的属性值集合， $D^v$ 表示属性值为 $v$ 的数据子集。求和项也称为条件熵，我们可以理解为它是先求出每个数据子集的信息熵，然后按每个数据子集占原数据集的比例来赋予权重，比例越大，对提升纯度的帮助就越大。