(算法理论)回溯法与与分支限界法（python）

分支限界法与回溯法的区别

1. 求解目标：回溯法的求解目标是找出解空间树中满足约束条件的所有解，而分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。
2. 搜索方式的不同：回溯法以深度优先的方式搜索解空间树，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。

分支限界法

核心思想：分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。
此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

常见的两种分支限界法

1. 队列式(FIFO)分支限界法:
   按照队列先进先出（FIFO）原则选取下一个结点为扩展结点。
2. 优先队列式分支限界法:
   按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。

通过实例问题来理解方法：

分支限定法解单源最短路径：

问题描述：

在下图所给的有向图G中，每一边都有一个非负边权。要求图G的从源顶点s到目标顶点t之间的最短路径。

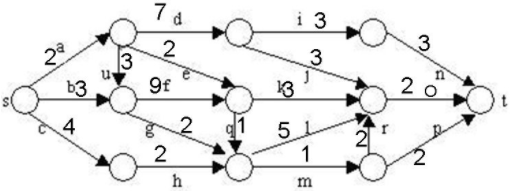
个人理解：
什么叫分支限界？用FIFO队列方法来说明：
一、将图G的单源最短路径问题分解为解空间树。其中，每一个结点旁边的数字表示该结点所对应的当前路长。
创建队列。

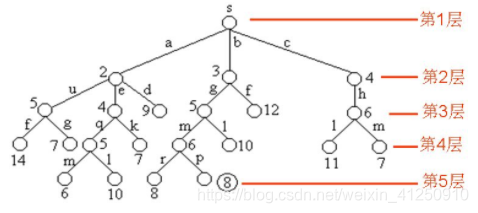
二、

1. 节点s入队列，Ｑ＝{ s }，我们取出队头节点，作为扩散节点，更新他的后代的值。
   　如图所示更新节点a，b，c的距离，并将他们加入队列，Ｑ＝｛s，a，b，c｝。 完成后节点s出队。
   　Ｑ＝｛a，b，c｝。
2. 同样，重复１的步骤，取出队头节点，a作为扩散节点，Ｑ＝｛a，b，c，u，e，d｝。完成后节点a出队。
   Ｑ＝｛b，c，u，e，d｝。
3. 同样，继续重复，取出队头节点，b作为扩散节点，Ｑ＝｛b，c，u，e，d，g，f｝。完成后节点b出队。
   Ｑ＝｛c，u，e，d，g，f｝。
4. 同样，继续重复，取出队头节点，c作为扩散节点，Ｑ＝｛c，u，e，d，g，f , h ｝。完成后节点c出队。
   Ｑ＝｛u，e，d，g，f , h ｝。
5. 当u作为扩散节点，f和g入队，我们发现f节点已经在队列中，这时比较：s—a—u—f 权重为14，s—b—f 权重为12，所以s—a—u—f这条路径就被剪枝掉了，之后我们不再考虑。 这就是“限界”（称为”剪枝“）的思想。
6. 重复步骤，直到Ｑ为空。

优先队列法方法和FIFO方法类似，区别在于优先队列每次取队列元素中到源点距离最短的点。

python实现源代码：

# 初始化图参数 用字典初始初始化这个图
G = {1: { 2: 4, 3: 2,4:5},
     2: { 5: 7, 6: 5},
     3