树（应用）

最新推荐文章于 2021-12-10 14:57:44 发布

weixin_40805072

最新推荐文章于 2021-12-10 14:57:44 发布

阅读量197

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构文章标签：哈夫曼树哈夫曼编码二叉排序树

本文链接：https://blog.youkuaiyun.com/weixin_40805072/article/details/98959215

数据结构专栏收录该内容

31 篇文章

订阅专栏

一、哈夫曼树和哈夫曼编码

1.基本概念

路径：指从树中一个结点到另一个结点的分支所构成的路线
路径长度：指路径上的分支数目
树的路径长度：从根到每个结点的路径长度之和
带权路径长度：结点具有权值，从该结点到根之间的路径长度乘以结点的权值，就是该结点的带权路径长度
树的带权路径长度（WPL）：树的带权路径长度是指树中所有叶子结点的带权路径长度之和

$WPL=\sum_{i=1}^{n}w_{i}l_{i}$ (wi为第i个带权叶子结点所带的权值，li是该叶结点到根结点的路径长度)

其中WPL最小的二叉树成为最优二叉树，也叫哈夫曼树

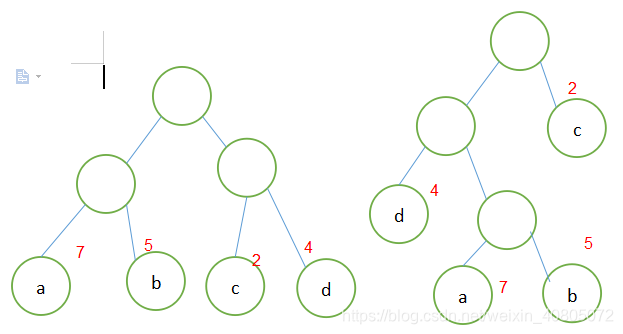
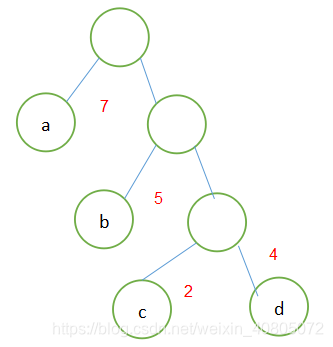
（1）wpl=7*2+5*2+2*2+4*2=36

（2）wpl=4*2+7*3+5*3+2*1=46

（3）wpl=7*1+5*2+2*3+4*3=35

图中三棵都有四个叶子结点，但第三个二叉树wpl最小，所以它为哈夫曼树

2.哈夫曼树的构造

（1）将n个结点分别作为n棵仅含一个结点的二叉树，构成森林F

（2）构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新结点的权值置为左、右子树上根结点的权值之和

（3）从F中删除刚才选出的两棵树，同时将得到的树加入F

（4）重复步骤（2）（3）直至F中只剩下一棵树为止

例：

（1）先将a,b,c,d看作只有根的4棵二叉树

（2）选出权值最小的两个根c和d，将它们作为左右子树，构造出新的二叉树。新的二叉树的根结点权值为c和d权值之和，原集合中删除c和d，同时将新构造的二叉树加入集合中

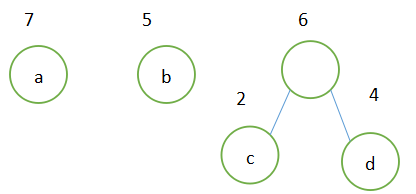
（3）继续选择权值最小的两个根，即权值为5和6的两个根结点，将它们作为左右子树，构造为新的二叉树，新的二叉树的根结点权值为11。在原集合删除5和6，同时将新构造的二叉树加入集合中

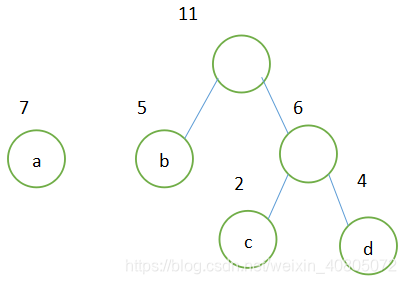
（4）继续选择权值最小的两个根，即权值为7和11的两个根，将它们作为左右子树木构造一棵新的二叉树，新的二叉树的根结点权值为7+11=18。原集合中删除根权值为7和11的两棵树。同时将新的树加入集合中

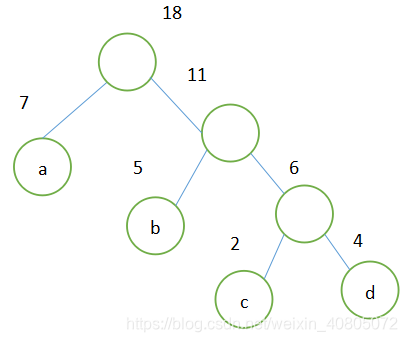
（5）此时集合只剩下一棵二叉树，这棵树就是哈夫曼树。wpl=35

3.哈夫曼树的特点

（1）权值越大的结点，距离根结点越近

（2）树中没有度为1的结点。这类树又叫正则二叉树

（3）树的带权路径长度最短

4.哈夫曼编码

对于待处理的一个字符串序列，若对每个字符用同样长度的二进制位表示，则称这种编码方式为固定长度编码。

哈夫曼树---->哈夫曼编码。

（1）将每个出现的字符当作一个独立的结点，其权值为它出现的频度（或次数），构造出对应的哈夫曼树。

字符的编码解释为：从根到该字符的路径上边标记的序列，其中边标记为0表示“转向左孩子”，标记为1表示“转向右孩子”。

矩形方块表示字符及其出现的次数。

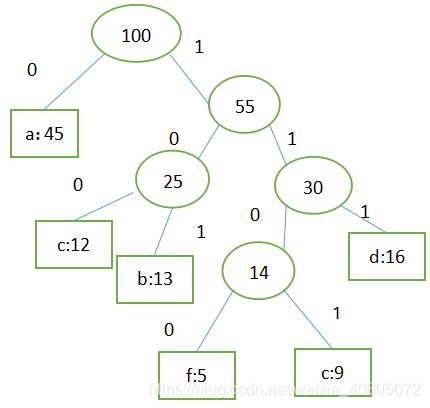
0，1表示左右子树无明确规定。因此左右结点顺序任意，所以哈夫曼树不唯一。

二、二叉排序树

1.二叉排序树

定义:（1）若左子树非空，则左子树所有结点关键字值均小于根结点关键字

（2）若右子树非空，则右子树所有结点关键字值均大于根结点关键字

（3）左右子树本身也是一棵二叉排序树

根据二叉排序的定义，知左子树结点值<根结点值<右子树结点指

所以对二叉树排序树进行中序遍历，可以得到一个递增的有序序列。

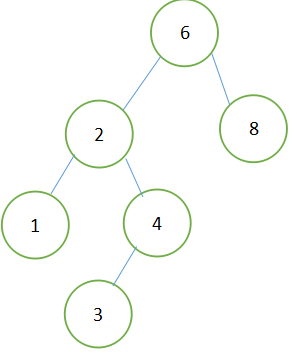中序遍历为123468

2.二叉排序树的查找

比如1中的图，查找值为4的结点。首先4与根结点6比较。因为4<6，所以在根结点的左子树继续查找。因为4>2所以在结点2的右子树中查找，查找成功。

递归算法

BTNode* BSTSearch(BTNode* bt,int key){
    if(bt==NULL)
        return NULL;
    else{
        if(bt->key==key)
            return bt;
    else if(key<bt->key)
            return BSTSearch(bt->lchild,key);
    else return BSTSearch(bt->rchild,key);
}
}

非递归算法

BSTNode *BST_search(BiTree T,Elemtype key,BSTNode *&p){
    p=NULL;
    while(T!=NULL&&key!=T->data){
        p=T;
        if(key<T->data)  T=T->child;
        else 
        T=T->rchild;
}
    return T;
}

3.二叉排序树的插入

插入过程：若原二叉树为空，则直接插入结点；

否则，若关键字k小于根结点关键字，则插入左子树，

若关键字k大于根结点关键字，则插入右子树。

int BST_Insert(BiTree &T,KeyType k){
        if(T==NULL){
            T=(BiTree)malloc(sizeof(BSTNode));
            T->key=k;
            T->lchild=T->rhild=NULL;
            return 1;
}
    else if(k==T->key)
        return 0;
    else if(k<T->key)        //插入T的右子树
        return BST_Insert(T->lchild,k);
    else                     //插入T的左子树                               
        return BST_Insert(T->rchild,k);
}