考研数据结构之查找（9.4）——二叉排序树（C表示）

概念

二叉排序树（BST）的定义：

二叉排序树或者是空树，或者是满足以下性质的二叉树:

1)若它的左子树不空，则左子树上所有关键字的值均不大于(不小于)根关键字的值。

2)若它的右子树不空，则右子树上所有关键字的值均不小于(不大于)根关键字的值。

3)左右子树又各是一棵二叉排序树。

例如：

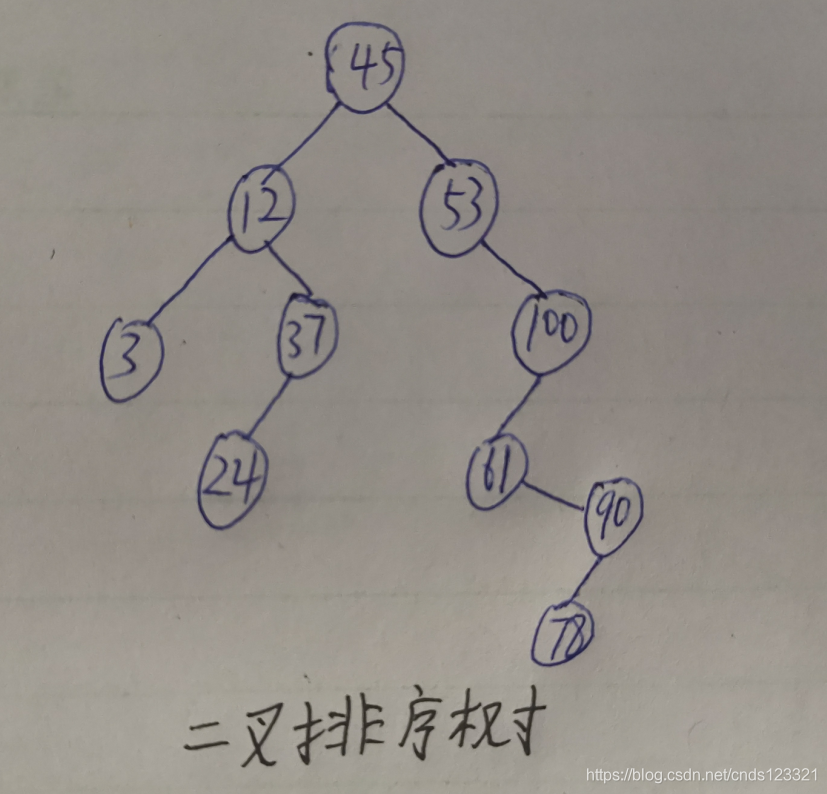
二叉排序树的存储结构：

二叉排序树通常采用二叉链表进行存储，其结点类型定义同一般的二叉树类似。

typedef struct BTNode {
	int key;// 代表关键字
	struct BTNode *lchild;
	struct BTNode *rchild;
} BTNode;

算法

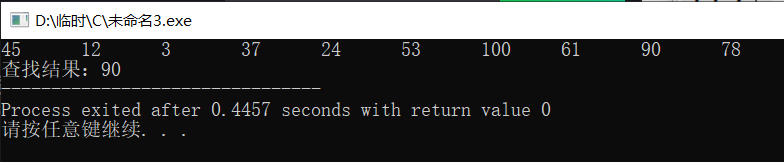
（1）查找关键字的算法

显然，要找的关键字要么在左子树上，要么在右子树上，要么在根结点上。由二叉排序树的定义可以知道，根结点中的关键字将所有关键字分成了两部分，即大干根结点中关键字的部分和小于根结点中关键字的部分。可以将待查关键字先和根结点中的关键字比较，如果相等则查找成功:如果小于则到左子树中去查找，无须考虑右子树中的关键字;如果大于则到右子树中去查找，无须考虑左子树中的关键字。如果来到当前树的子树根，则重复上述过程:如果来到了结点的空指针域，则说明查找失败。可以看出这个过程和折半查找法十分相似，实际上折半查找法的判定树就是-棵二叉排序树。

代码如下：

/* 查找关键字的算法 */
BTNode * BSTSearch(BTNode *bt,int key) {
	if(bt==NULL) { // 来到了空指针域，查找不成功返回NULL
		return NULL;
	} else {
		if(bt->key==key) {
			return bt;// 等于根结点中的关键字，查找成功，返回关键字所在的结点指针
		} else if(key<bt->key) { // 小于根节点中的关键字到左子树中查找
			return BSTSearch(bt->lchild,key);
		} else { // 大于根节点中的关键字的时候到右子树中查找
			return BSTSearch(bt->rchild,key);
		}
	}
}

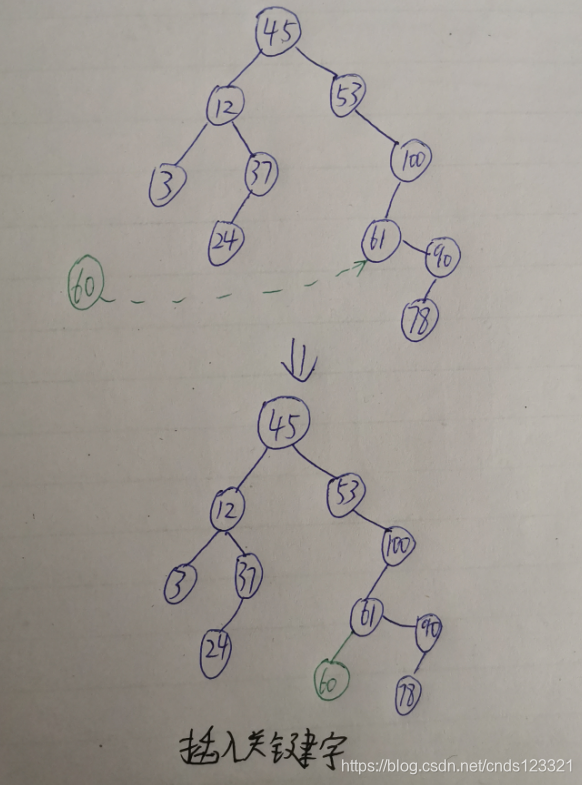
（2）插入关键字的算法

二叉排序树是一个查找表，插入一个关键字首先要找到插入位置。

对于一个不存在于二叉排序树中的关键字，其查找不成功的位置即为该关键字的插入位置。

因此只需要将查找关键字的算法修改，在来到空指针的时候将关键字插入即可。在插入的过程中，如果待插入关键字已经存在，则返回0，代表插入不成功；如果待插入关键字不存在，则插入，并返回1，代表插入成功。

图解：

代码如下：

/* 插入关键字 */
/* *&bt指的是二叉树；key指的是关键字 */
int BSTInsert(BTNode *&bt,int key) {
	if(bt==NULL) { // 当前为空指针时说明找到插入位置，创建新结点进行插入
		bt=(BTNode *)malloc(sizeof(BTNode));// 创建新结点
		bt->lchild=NULL;
		bt->rchild=NULL;
		bt->key=key;// 将待插关键字存入新结点中，插入成功返回1
		return 1;
	} else { // 如果结点不空，则查找插入位置
		if(key==bt->key) { // 关键字已存在于树中，查找失败，返回0
			return 0;
		} else if(key<bt->key) {
			return BSTInsert(bt->lchild,key);
		} else {
			return BSTInsert(bt->rchild,key);
		}
	}
}

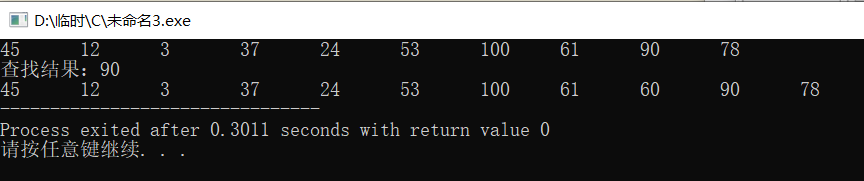
注意：是先序遍历输出序列结果。

（3）二叉排序树的构造算法

只需要建立一棵空树，然后将关键字逐个插入到空树中即可构造一棵二叉排序树。

关键字在数组key[]中。

/* 构建二叉排序树 */
/* *&bt指的是二叉排序树；key[]指的是关键字数组；n指的是数组长度 */
void CreateBST(BTNode *&bt,int key[],int n) {
	bt=NULL;// 将树清空
	for(int i=0; i<n; i++) {
		BSTInsert(bt,key[i]);
	}
}

（4）删除关键字的操作

当在二叉排序树中删除一个关键字时，不能把以该关键字所在的结点为根的子树都删除，而是只删除这一个结点，并保持二叉排序树的特性。

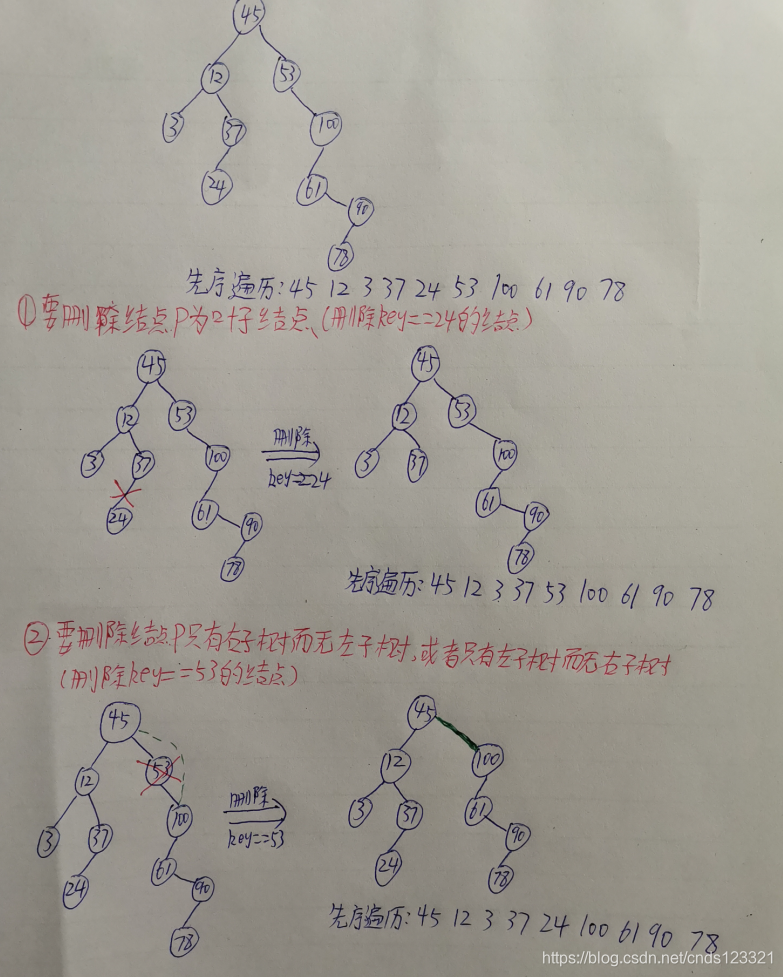
假设在二叉排序树，上被删除结点为p, f为其双亲结点，则删除结点p的过程分为以下3种情况。

• 1) p结点为叶子结点。由于删除叶子结点后不会破坏二叉排序树的特性，因此直接删除即可。
• 2) p结点只有右子树而无左子树，或者只有左子树而无右子树。此时只需将p删掉，然后将p的子树直接连接在原来p与其双亲结点f相连的指针上即可。
• 3) p结点既有左子树又有右子树。此时可以将这种情况转化为1)或2)中的情况，做法为:先沿着p的左子树根结点助右指针一直住右走 直到来到其布子树的最右边的一个结点r (也可以沿着p的右子树根结点的左指针一直往左走，中的关键字代替。最后判断，如果r是叶子结点，，是到来到其左于树的最左边的 个结点)、然后将p中的关键字用r， 则按照1)中的方法删除，r;如果r是非叶子结点，则(此时的 r不可能是有两个子树的结点)。

图解：

代码如下：

int Delete(BTNode *&p) {
	// 从二叉排序树中删除结点p，并重接它的左或右子树
	BTNode *q,*s;
	if(!p->rchild) { // 右子树空则只需重接它的左子树
		q=p;
		p=p->lchild;
		free(q);
		return 1;
	} else if(!p->lchild) { // 只需重接它的右子树
		q=p;
		p=p->rchild;
		free(q);
		return 1;
	} else { // 左右子树均不空
		q=p;
		s=p->lchild;
		while(s->rchild) {
			q=s;
			s=s->rchild;
		}
		p->key=s->key;
		if(q!=p) {
			q->rchild=s->lchild;
		} else {
			q->lchild=s->lchild;
		}
		return 1;
	}
	return 0;
}

/* 删除二叉树结点 */
int DeleteBST(BTNode *&bt,int key) {
	// 若二叉排序树中存在关键字等于key的数据元素时，则删除该数据元素结点
	if(!bt) { // 不存在关键字等于Key的元素
		return 0;// 删除失败返回0
	} else {
		if(bt->key==key) {
			Delete(bt);// 找到关键字等于key的元素
		} else if(key<bt->key) {
			return DeleteBST(bt->lchild,key);
		} else {
			return DeleteBST(bt->rchild,key);
		}
	}
}

完整代码如下：

#include<stdio.h>
#include<stdlib.h>

typedef struct BTNode {
	int key;// 代表关键字
	struct BTNode *lchild;
	struct BTNode *rchild;
} BTNode;

/* 查找关键字的算法 */
BTNode * BSTSearch(BTNode *bt,int key) {
	if(bt==NULL) { // 来到了空指针域，查找不成功返回NULL
		return NULL;
	} else {
		if(bt->key==key) {
			return bt;// 等于根结点中的关键字，查找成功，返回关键字所在的结点指针
		} else if(key<bt->key) { // 小于根节点中的关键字到左子树中查找
			return BSTSearch(bt->lchild,key);
		} else { // 大于根节点中的关键字的时候到右子树中查找
			return BSTSearch(bt->rchild,key);
		}
	}
}

/* 插入关键字 */
/* *&bt指的是二叉树；key指的是关键字 */
int BSTInsert(BTNode *&bt,int key) {
	if(bt==NULL) { // 当前为空指针时说明找到插入位置，创建新结点进行插入
		bt=(BTNode *)malloc(sizeof(BTNode));// 创建新结点
		bt->lchild=NULL;
		bt->rchild=NULL;
		bt->key=key;// 将待插关键字存入新结点中，插入成功返回1
		return 1;
	} else { // 如果结点不空，则查找插入位置
		if(key==bt->key) { // 关键字已存在于树中，查找失败，返回0
			return 0;
		} else if(key<bt->key) {
			return BSTInsert(bt->lchild,key);
		} else {
			return BSTInsert(bt->rchild,key);
		}
	}
}

/* 构建二叉排序树 */
/* *&bt指的是二叉排序树；key[]指的是关键字数组；n指的是数组长度 */
void CreateBST(BTNode *&bt,int key[],int n) {
	bt=NULL;// 将树清空
	for(int i=0; i<n; i++) {
		BSTInsert(bt,key[i]);
	}
}

int Delete(BTNode *&p) {
	// 从二叉排序树中删除结点p，并重接它的左或右子树
	BTNode *q,*s;
	if(!p->rchild) { // 右子树空则只需重接它的左子树
		q=p;
		p=p->lchild;
		free(q);
		return 1;
	} else if(!p->lchild) { // 只需重接它的右子树
		q=p;
		p=p->rchild;
		free(q);
		return 1;
	} else { // 左右子树均不空
		q=p;
		s=p->lchild;
		while(s->rchild) {
			q=s;
			s=s->rchild;
		}
		p->key=s->key;
		if(q!=p) {
			q->rchild=s->lchild;
		} else {
			q->lchild=s->lchild;
		}
		return 1;
	}
	return 0;
}

/* 删除二叉树结点 */
int DeleteBST(BTNode *&bt,int key) {
	// 若二叉排序树中存在关键字等于key的数据元素时，则删除该数据元素结点
	if(!bt) { // 不存在关键字等于Key的元素
		return 0;// 删除失败返回0
	} else {
		if(bt->key==key) {
			Delete(bt);// 找到关键字等于key的元素
		} else if(key<bt->key) {
			return DeleteBST(bt->lchild,key);
		} else {
			return DeleteBST(bt->rchild,key);
		}
	}
}

/* 先序遍历 */
/* *p指的是二叉树的根节点 */
void preOrder(BTNode *p) {
	if(p!=NULL) {
		printf("%d\t",p->key);// 打印树结点的数据
		preOrder(p->lchild);// 先序遍历左子树
		preOrder(p->rchild);// 先序遍历右子树
	}
}

int main() {
	int nums[]= {45,12,53,3,37,100,24,61,90,78};
	int n=10;// nums数组的长度

	BTNode *bt;
	CreateBST(bt,nums,n);// 构建二叉排序树
	preOrder(bt);// 先序遍历二叉排序树

//	/* 查找关键字 */
//	BTNode *searchR;
//	searchR=BSTSearch(bt,90);
//	printf("\n查找结果：%d",searchR->key);
//
//	/* 插入关键字 */
//	BSTInsert(bt,60);
//	printf("\n");
//	preOrder(bt);

	/* 删除关键字 */
	DeleteBST(bt,45);// 删除key为45的关键字结点
	printf("\n");
	preOrder(bt);

	return 0;
}