决策树

决策树学习算法包含特征选择、决策树的生成与决策树的剪枝。
一、ID3、C4.5
1、特征选择（利用信息增益准则）
1）信息增益
特征A对训练数据集D的信息增益g（D，A），定义为集合D的经验熵H（D）与特征条件下D的经验条件熵H（D|A）之差。
即 g（D，A）=H(D) - H(D | A)
一般的，熵H（Y）与条件熵H（Y|X）之差称为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。

信息增益的算法：

（1）数据集D中的类别有K个，属于K的类别的个数用|Ck|，|D|表示数据总数。则数据D的经验熵为H（D）。
（2）在特征A的作用下D被分为了i个D集合，则|Di|/|D|表示第i个D集合占比。在Di的子集中又有K个类别。则有H(D|A)得出。

信息增益比：
由于以信息增益作为划分训练集的特征，存在偏向于选择取值较多的特征的问题（因为当取值较多时么个Di中的数据很少，造成上图中（2）式的log项为0，从而使得最终的信息增益最大），而是用信息增益比可以对这一问题进行校正。

取值越多Ha（D）越大（log项后越大），此时虽然g（D，A）也越大，但因为Ha（D）的牵制，最终结果被调和了。

2、决策树的生成
3、决策树的剪枝
决策树的剪枝往往通过极小化决策树整体的损失函数来实现。损失函数定义为：

|T|为树T的叶节点个数，t是树T的叶节点，叶节点t有Nt个样本点，其中k类的样本点有Ntk个，Ht（T）为叶节点t上的经验熵。α》=0.
C(T)表示模型对训练数据的预测误差，即模型与训练数据的拟合程度。|T|表示模型复杂度，α控制两者之间的影响。

树的剪枝算法：
1）计算每个节点的经验熵。
2）递归地从树的叶节点向上回缩。
3）设Tb和Ta分别对应回缩到父节点的前与后的整体树，那么如果Cα（Ta）<=Cα（Tb)，那么将父节点变为新的叶节点，重复操作2），直至不能继续。

二、CART算法
1、回归树的生成：
在训练数据集所在的输入空间，递归地将每个区域划分为两个子区域并决定每个子区域上的输出值。
1）选择最优切分变量j与切分点s：

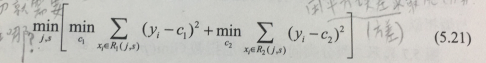
遍历变量j，对固定的切分变量j扫描切分点s，选择使式（5.21）最小值得对（j，s）。
2）对选定的对（j，s）划分区域并决定相应的输出值：

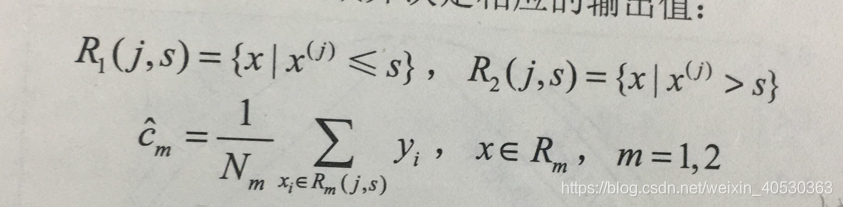
R表示区域，c表示该区域的平均值
3）继续1),2)步骤，直至满足停止条件（什么停止条件？）。
4）将输入空间划分为M个区域R1，…Rm。生成决策树：

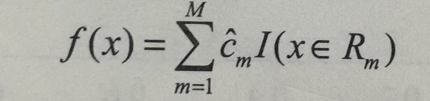
2、分类树的生成
1）基尼指数定义：


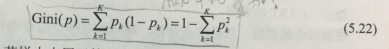
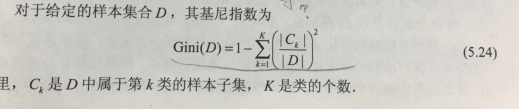
如果集合D根基特征A被划分为D1、D2两部分，则在特征A的条件下，集合D的基尼指数为：

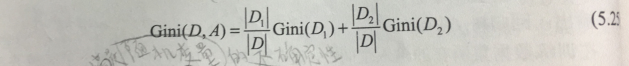
基尼指数越大（5.25式可以看出来是Gini（D）越大造成的，而其由（5.24）的第二项中每个Ck/D很小造成的）也就是说几率过于分散而导致的分类问题更难通过该特征下的类别分布区分开。样本集合的不确定性越大，这与熵相似。

2）CART生成算法

（3）对两个子节点递归的调用（1）（2）直至满足条件，这里的条件为：
一则是已生成的树中叶节点的样本个数已经小于预设的阈值，无法再划分下去了
二则是节点中计算gini指数已经小于预设阈值了，这说明该叶节点的数据集中特征划分后的类别基本属于同一类了。
最终生成CART决策树。

3、CART的剪枝

定义了两个损失函数,可视作剪枝后与剪枝前的两个损失。

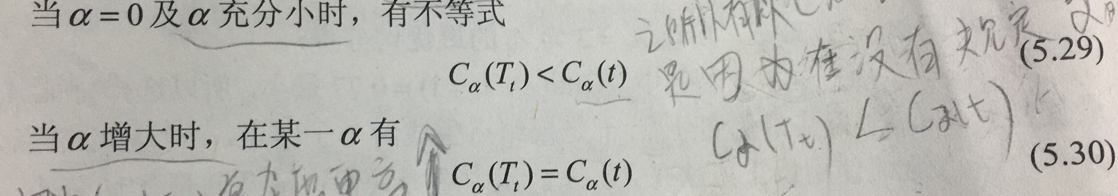
（5.29）的意思是在不看重树的复杂度的情况下，划分后生成都树比划分前的损失函数会小些。
（5.30）表示，但是当看重复杂度时（α增大了），Cα（Tt）损失也会随之上升，因为后一项的值在不断增大。从而到最后赶上了Cα（t）的损失。由此我们可以得出：当我们看重复杂度时，有存在（5.30）式，那为何不选一个更简洁的树呢？

为此通过式（5.27,5.28,5.30）得到：

此处之所以要选择减少程度最小的那个Tt进行剪枝，是因为在生成决策树时，通过规则进行划分并形成叶节点后，其损失函数并没有减少很多（此处是有一个阈值判断是否生成的），那么此次的分裂其实在剪枝操作中就可以视作为不太必要的分裂，因为其增加了树的复杂度。

！CART算法详细过程

此种算法自动选择除了参数α！