
周期信号的傅里叶级数
周期信号三角形式的傅里叶级数
1.三角形式的傅里叶级数

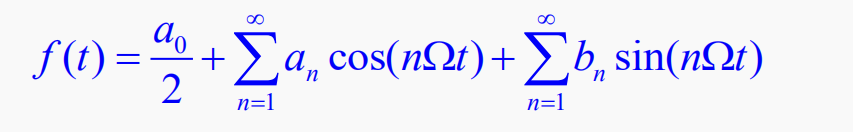
系数an, bn称为傅里叶系数

2.狄里赫利(Dirichlet)条件:
条件1:在一个周期内,函数连续或只有有限个第一类间断点;
条件2:在一个周期内,函数极大值和极小值的数目应为有限个;
条件3:在一个周期内,函数绝对可积。
3.余弦形式的傅里叶级数


含义:周期信号可分解为直流和许多余弦分量

例:将图示方波信号f(t)展开为傅里叶级数

解:
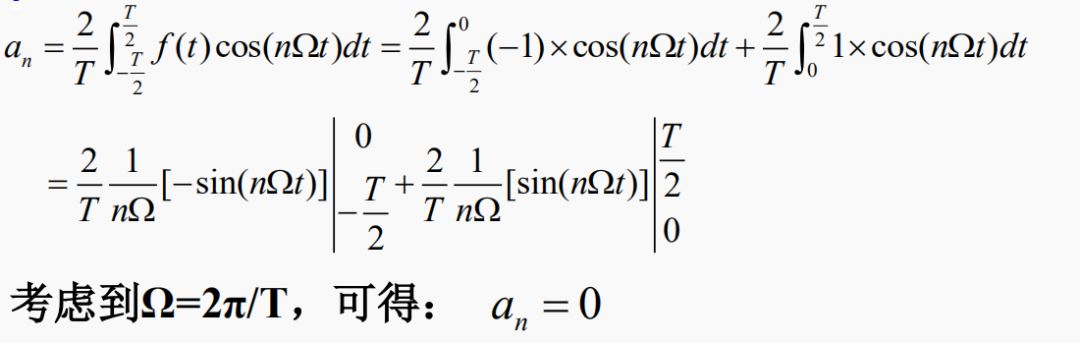

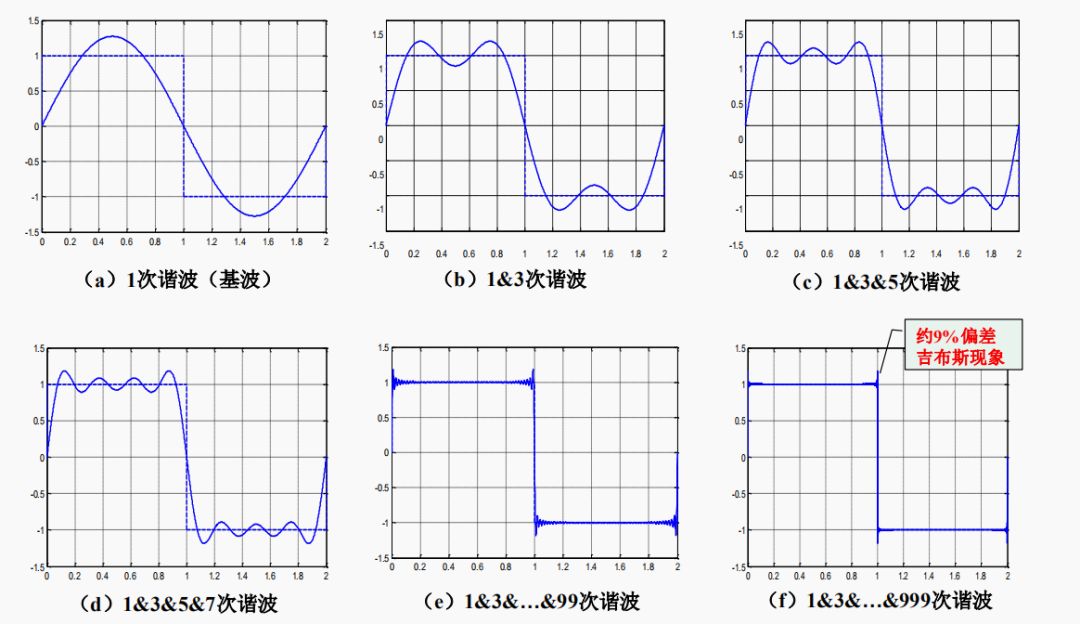
4.吉布斯现象
用有限项傅里叶级数表示有间断点的信号时,在间断点附近不可避免的会出现振荡和超调量。超调量的幅度不会随所取项数的增加而减小。只是随着项数的
增多,振荡频率变高,并向间断点处压缩,从而使它所占有的能量减少。
当选取的项数很大时,该超调量趋于一个常数,大约等于总跳变值的9%,并从间断点开始以起伏振荡的形式逐渐衰减下去。这种现象称为吉布斯现象。
周期信号波形对称性和谐波特性
1 . f(t)为偶函数——对称于纵轴 f(t) =f(-t)

2 . f(t)为奇函数——对称于原点 f(t) =-f(-t)
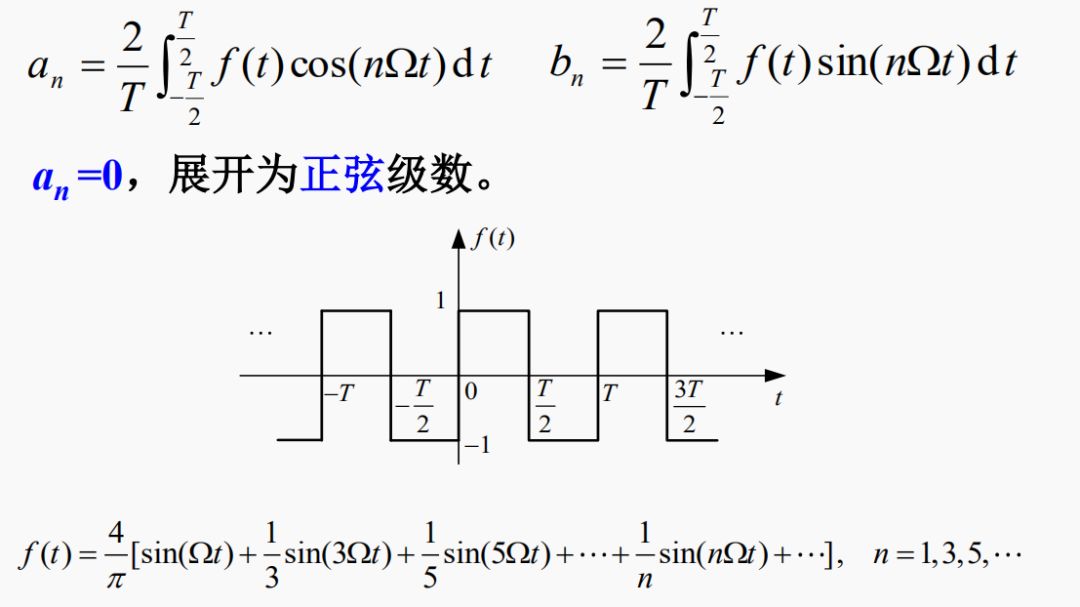
3 . f(t)为奇谐函数——f(t) = –f(t±T/2)
其傅里叶级数中只含奇次谐波分量,而不含偶次谐波分量,即:


4 . f(t)为偶谐函数——f(t) = f(t±T/2)
其傅里叶级数中只含偶次谐波分量,而不含奇次谐波分量,即:

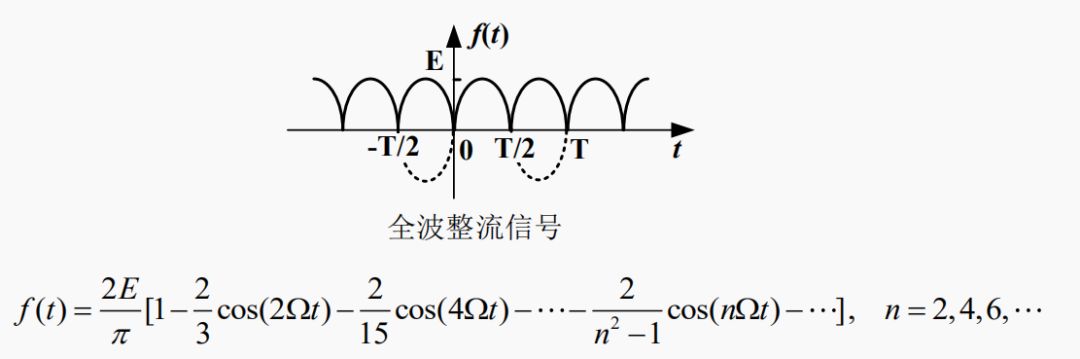
指数形式的傅里叶级数
三角形式的傅里叶级数,含义比较明确,但运算常感不便,因而经常采用指数形式的傅里叶级数。


指数形式的傅里叶级数
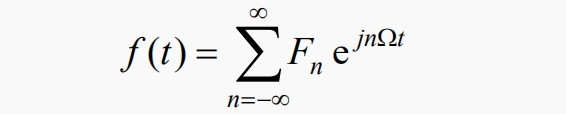
复傅里叶系数

表明:任意周期信号f(t)可分解为许多不同频率的虚指数信号之和。
Fn 是频率为nΩ的分量的系数,F0= A0/2为直流分量
例:求如图所示周期信号的指数形式的傅里叶级数

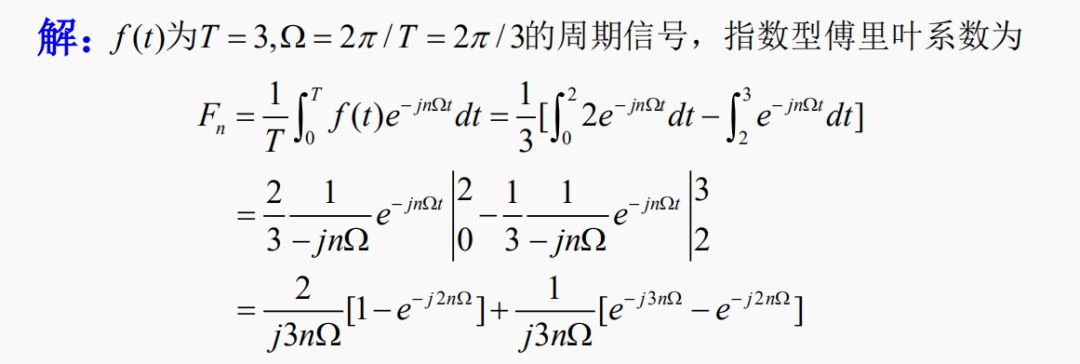
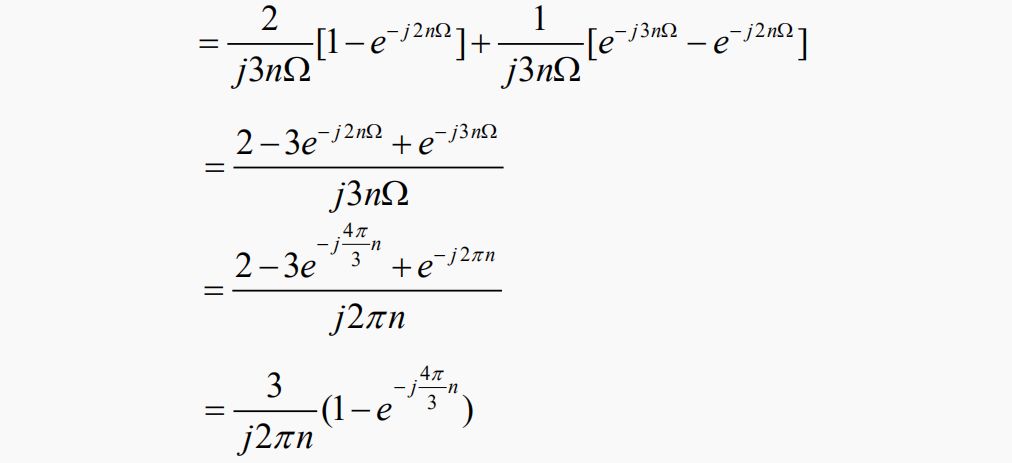
指数形式的傅里叶级数为:

两种傅里叶级数展开形式的关系
三角形式的傅里叶级数:
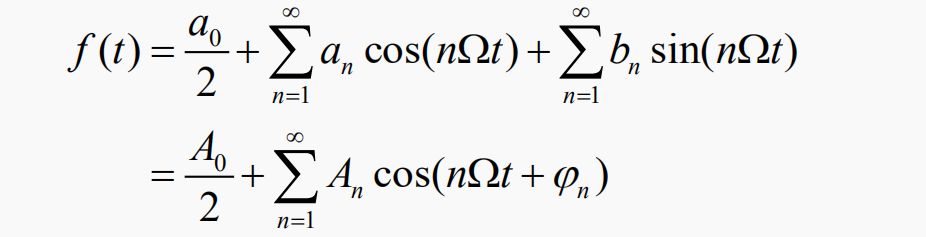
指数形式的傅里叶级数:


NUM460

个人博客式公众号

用心每一天
























 1722
1722

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








