GAMES101-计算机图形学入门 LEC4: TRANSFORMATION-3D

本节课程视频地址：https://www.bilibili.com/video/BV1X7411F744/?p=4

补充上一节课的一个内容，旋转矩阵的逆矩阵是它的转置，也就是说有$R_{-\theta }=R_{\theta }^{-1}=R_{\theta }^T$

上节课讲了，二维变换中的绕原点的旋转、缩放、切变，以及齐次坐标，还有通过简单变换组合成复杂变换。

这节课先讲三维变换，然后讲困难且重要的观测变换（Viewing Transformation）

三维变换（3D Transformation）

三维的齐次坐标：

• 点：$(x,y,z,1{)}^T$
• 向量：$(x,y,z,0{)}^T$

注：(x,y,z,w)其中w!=0 表示的是点(x/w,y/w,z/w)

齐次坐标使用4维矩阵来表示仿射变换：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}a& b& c& t_x\\ d& e& f& t_y\\ g& h& i& t_z\\ 0& 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$
注：仿射变换中是先线性变换（也就是绕原点所作的变换）再平移变换。

缩放

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}{s}_x& 0& 0& 0\\ 0& s_y& 0& 0\\ 0& 0& s_z& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

平移

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

旋转

三维的旋转分为绕x轴旋转、绕y轴旋转和绕z轴旋转。

$$R_x(\alpha )=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\alpha & -sin\alpha & 0\\ 0& sin\alpha & cos\alpha & 0\\ 0& 0& 0& 1\end{array}\right]$$
$$R_y(\alpha )=\left[\begin{array}{cccc}cos\alpha & 0& sin\alpha & 0\\ 0& 1& 0& 0\\ -sin\alpha & 0& cos\alpha & 0\\ 0& 0& 0& 1\end{array}\right]$$
$$R_z(\alpha )=\left[\begin{array}{cccc}cos\alpha & -sin\alpha & 0& 0\\ sin\alpha & cos\alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

注意旋转矩阵$R_y(\alpha )$的$sin\alpha$的正负号是和另外两个相反的。其实没有反，因为这是一个右手系的坐标轴，绕x轴逆时针旋转的方向是在y0z平面中y轴旋转到z轴的方向，绕z轴旋转的方向是在x0y平面中x轴旋转到y轴的方向，而绕y轴旋转的方向在z0x平面中是从z轴旋转到x轴的方向。以x0y平面的旋转为例：$x^{\prime }=xcos\alpha -ysin\alpha$，即要得到$x^{\prime }$需要乘上y轴原始坐标的$-sin\alpha$。所以在z0x平面内，要得到z轴所在坐标：$z^{\prime }=zcos\alpha -xsin\alpha$。清晰的记忆方法，以绕x轴旋转为例，绕x轴旋转在y0z平面内是从y轴到z轴的方向，$y^{\prime }=y\cos \alpha -z\sin \alpha$即转离y轴的方向就减，$z^{\prime }=y\sin \alpha +z\cos \alpha$ 即朝z轴转的方向就加。

Rodrigues 旋转公式

绕旋转轴 $\vec{n}$ 旋转角度 $\alpha$：

形式一：
$$R(\vec{n},\alpha )=cos(\alpha )I+(1-cos(\alpha ))\vec{n}\cdot {\vec{n}}^T+\sin \alpha \cdot \left[\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right]$$
形式二：
$$R(\vec{n},\alpha )=I+\sin \alpha \cdot \left[\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right]+(1-cos(\alpha ))\cdot {\left[\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right]}^2$$

证明：

https://www.cnblogs.com/wtyuan/p/12324495.html

观测变换 (Viewing transformation)

视图变换 (View transformation)

什么是视图变换

想象一下拍照：

• 首先要找一个好的背景，把人的位置和人与背景的相对位置安排好（模型变换）；
• 然后要找一个好的角度（视图变换）；
• 最后按快门（投影变换）。

定义相机：

1. 位置向量 Postion: $\vec{e}$
2. 朝向 Look-at direction: $\vec{g}$
3. 相机向上的方向 Up direction (垂直于朝向) : $\vec{t}$

约定：相机永远放在原点，相机永远以+y为向上方向，相机永远朝-z方向看。 也就是进行视图变换时要将所有对象和相机一起做变换，直到相机在原点，朝向-z，以+y为正方向。

如何将相机从它原来的位置移到约定位置

1. 平移 $\vec{e}$到原点；
2. 旋转 $\vec{g}$ 到 -z 方向；
3. 旋转 $\vec{t}$ 到 +y 方向
4. 旋转 $\vec{g}\times \vec{t}$ 到 +x 方向

如何求出将相机旋转到约定位置的旋转矩阵？

先平移到原点:
$$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$$

再考虑它的逆旋转，找到三个特殊向量的旋转，即 $\hat{x}$ 到 $\hat{g}\times \hat{t}$, $\hat{y}$ 到 $\hat{t}$，$\hat{z}$ 到 $-\hat{g}$，就能找到这个逆旋转的旋转矩阵：

$$R_{review}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_{\hat{t}}& x_{-\hat{g}}& 0\\ y_{\hat{g}\times \hat{t}}& y_{\hat{t}}& y_{-\hat{g}}& 0\\ z_{\hat{g}\times \hat{t}}& z_{\hat{t}}& z_{-\hat{g}}& 0\\ 0& 0& 0& 1\end{array}\right]$$
旋转矩阵是正交矩阵，上面这个矩阵显然符合，旋转矩阵的逆矩阵就是它的转置：
$$R_{review}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_{\hat{t}}& y_{\hat{t}}& z_{\hat{t}}& 0\\ x_{-\hat{g}}& y_{-\hat{g}}& z_{-\hat{g}}& 0\\ 0& 0& 0& 1\end{array}\right]$$

总结：将所有对象和相机一起做变换，直到相机在原点，朝向-z，以+y为正方向。

这就是视图变换。

投影变换（Perspective Projection）

正交投影（Orthographic projection）

透视投影（Perspective projection）

区别：正交投影没有近大远小而透视投影有。

正交投影

做法一：

假设已经进行了视图变换（即相机在原点，朝向-z，以+y为向上方向）

第一步，把所有点的z坐标变为0；

第二步，将得到的二维平面坐标做平移和缩放，让它们装在$[-1,-1{]}^2$ 这个正方形里。（至于为什么要进行这一步操作，这是一个约定俗成的办法，可以方便之后的操作）

做法二：(正规做法）

实际的计算机图形学操作中，还有一个比简单地把z扔掉更方便的做法：

同样，假设已经进行了视图变换（即相机在原点，朝向-z，以+y为向上方向）

假设此时所有物体装在一个 $[l,r]\times [b,t]\times [f,n]$ 的长方体内，将这个长方体映射到 $[-1,1{]}^3$ 的正方体：

先平移，再缩放：
$$M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

透视投影

回顾齐次坐标的一个重要性质：

$(x,y,z,1)$表示一个点，

$(kx,ky,kz,k!=0)$也表示该点，

$(xz,yz,z^2,z!=0)$也表示该点。

做法：

将一个截头锥体，“挤压”到一个长方体：

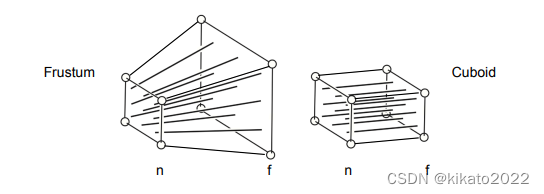
如何“挤压”呢？
提前告诉你，这个“挤压”可以用一个矩阵表示，一般叫投影变换矩阵，那么这个矩阵怎么求呢？

观察，该“挤压”的特点：
对于该截头锥体内部和表面的任意一点，x坐标和 y坐标很明显根据z坐标的大小有相似关系：

所以平移变换矩阵要做的第一件事情就是把所有对应的点x坐标和y坐标调整到与近平面上的那一点相同：
$$y^{\prime }=\frac{n}{z}y,x^{\prime }=\frac{n}{z}x$$
z坐标怎么变目前还不知道，用齐次坐标表示：
$$\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\to \left[\begin{array}{c}nx/z\\ ny/z\\ unknown\\ 1\end{array}\right]==\left[\begin{array}{c}nx\\ ny\\ stillunknown\\ z\end{array}\right]$$
这样已经可以得到这个变换矩阵的一大部分了：
$$M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right]$$

那么该矩阵的第三行怎么求？

利用两点：

1. 近平面上的点不会发生改变
   $$\left[\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right]\to \left[\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right]==\left[\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right]$$
   因为$n^2$与$x、y$无关，所以第三行的第一个和第二个元素是0，也就是说对于透视投影矩阵的第三行有：
   $$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]\left[\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right]=n^2$$

2. 远平面上与z轴相交的点不会改变
   $$\left[\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right]\to \left[\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right]==\left[\begin{array}{c}0\\ 0\\ f^2\\ f\end{array}\right]$$
   也就是：
   $$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]\left[\begin{array}{c}0\\ 0\\ f^2\\ f\end{array}\right]=f^2$$

可以建立方程组求解A和B了：
$$\begin{gathered} An+B=n^2 \\ Af+B=f^2 \end{gathered}$$
解得
$$A=n+f,B=-nf$$

得到该矩阵为：
$$M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& n& 0\end{array}\right]$$

最后
$$M_{persp}=M_{ortho}{M}_{persp\to ortho}$$

问题：对于截头锥体中间的点，它的z坐标怎么变？

$$\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& n& 0\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}nx\\ ny\\ nz+fz-nf\\ z\end{array}\right]$$

记
$$f(z)=\frac{nz+fz-nf}{z}-z=\frac{1}{z}[-z^2+(n+f)z-nf]，(n<z<f)$$
对于中括号中的二次函数，开口向下，且两个零点为z=f和z=n，所以中括号中的二次函数在f<n<z这个区间里大于0，又z<0，所以f(z)小于0，即z的坐标会变小(朝远平面方向变）。