多因素方差分析_简要回顾方差分析（ANOVA）

本次回顾主要从以下几个方面进行：

1. 方差分析是什么
2. 类别有多少种
3. 其原理是什么
4. 使用条件
5. 假设检验步骤
6. 相关sas代码

方差分析（Analysis of variance）是应用最广的统计方法之一。方差分析问题的提出最早可追溯到18世纪到19世纪，拉普拉斯(Pierre-Simon Laplace，1749年3月23日-1827年3月5日)、高斯(Carolus Fridericus Gauss，1777年4月30日-1855年2月23日)等著名数学家在提出假设检验(hypothesis testing)时候就为方差分析提出做了前瞻性贡献。20世纪初，费希尔(Ronald Aylmer Fisher, 1890年2月17日- 1962年7月29日) 首次提出方差分析，由多名研究者将其拓展。方差分析研究的并不是方差，而是均值的变异，即推断多个总体的均数是否有差别。

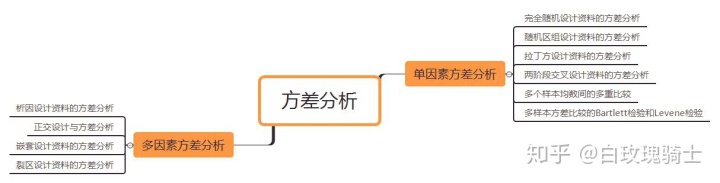
方差分析分为单因素的方差分析、多因素试验资料的方差分析。前者可分为完全随机设计资料的方差分析、随机区组设计资料的方差分析、拉丁方设计资料的方差分析、两阶段交叉设计资料的方差分析、多个样本均数间的多重比较、多样本方差比较的Bartlett检验和Levene检验。后者则有析因设计资料的方差分析、正交设计与方差分析、嵌套设计资料的方差分析、裂区设计资料的方差分析等。

方差分析常见分类

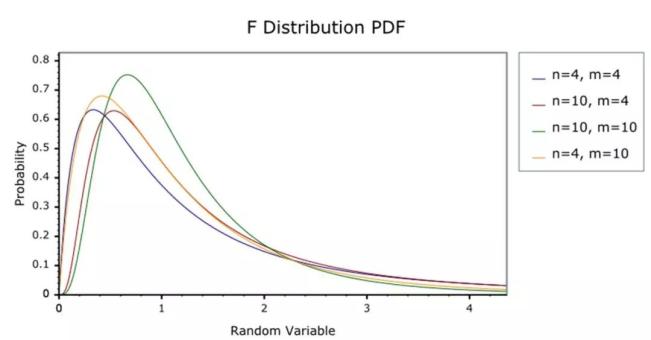
使用条件：1、样本服从正态分布；2、样本相互独立；3、方差齐

单因素方差分析

完全随机设计(completely random design)：随机指派是任意一次指派与任意其他指派是等可能的。比较p个处理均值的完全随机化设计是将处理随机指派给试验单位，或从p个总体中额每一个抽取独立随机样本^[1]。

随机区组设计(randomized block design)：又称配伍组设计，是配对设计的扩展。做法是：先按影响实验结果的非处理因素（如性别、体重、年龄、职业、病情、病程等）将实验对象配成区组（block），再分别将各区组内的实验对象随机分配到各处理组或对照组^[2]。

拉丁方设计(Latin square design)：实验研究涉及一个处理因素和两个控制因素，每个因素的类别数或水平数相等，此时可采用拉丁方设计来安排实验，将两个控制因素分别安排在拉丁方设计的行和列上^[3]。

两阶段交叉设计(crossover design)：在医学研究中，欲将A、B两种处理先后施加于同一批实验对象，随机地使半数实验对象现接受A后接受B，而另一半实验对象则正好相反，即先接受B再接受A^[4]。

多因素方差分析

析因设计(factorial experiment)<