卡方分布的期望和方差_数理统计第五讲（三大分布）

2.4常用分布与分布族（续）

接下来介绍统计中的三大分布，它们分别是

分布，

分布以及

分布，对于每个分布我们都将从以下四个方面进行介绍：

• 构造型定义（充要性）很重要！
• 概率密度函数
• 性质
• 上分位数

※

分布

构造型定义

设

，则

的分布为具有自由度

的

分布,记作

或

反之，如果随机变量

服从

，那么一定能找到

使得

这也就是构造型定义的充要性质，在介绍其他分布的构造型定义时将不再赘述.

概率密度函数

分布的密度为

在自由度变化时，密度函数的如图所示

卡方分布密度函数

下面给出密度函数的推导：

设

，只需证明

.

而根据

分布的可加性只需证明

.

记

的分布函数为

，其支撑为

,其支撑内有

进而得到密度函数为

因此

，进而

.

性质

可加性

设

且相互独立，则

这是因为

分布是

分布的特例，且

分布具有可加性

数字特征与特征函数

设

，根据

分布的期望方差能够得到

同理还能得到特征函数为

.

※

分布

构造型定义

设

且二者独立，则

的分布称为自由度为

的

分布，记作

或

.

概率密度函数

分布的密度为（好复杂啊，可以扔掉它吗？可以的！）

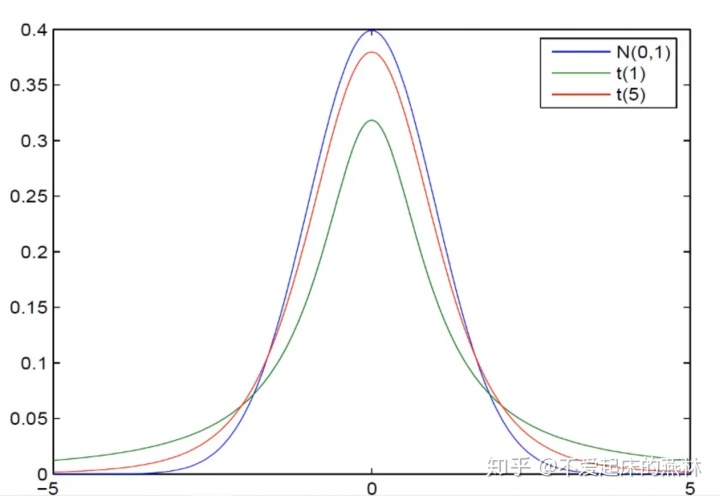
在自由度变化时，密度函数的如图所示

t分布密度函数

性质

定理T1 设

来自总体

，

为样本均值，

为样本方差，则

证明 利用构造型定义，想办法分子弄出正态，分母弄出卡方

且之前证过

与

独立，因此

这个结论可以与

一同记忆，

是将

换成了

.

这个定理对

分布的发现起着重要作用，当时人们认为正态可以做任何事情，

Pearson等统计学家都认为

是服从标准正态的，但是

W. S. Gosset发现在小样本场合，把

看作是正态的，会造成比较大的误差，进而他推导出了

定理T1，这个发现使得人们进一步深入地研究抽样分布，并产生了丰富的成果。

定理T2

设

,

即两个正态总体的方差是相同的，且假设

与

相互独立，记

为

的样本均值和样本方差，

是

的样本均值和样本方差，并记

那么

证明 看到样本均值和总体均值就要想到标准正态，看到样本方差就要想到卡方分布！

同一总体的样本均值与样本方差都独立了，不同独立总体的当然更加独立啦，所以

其中

也称为合样本方差，

也称为合样本标准差.

定理T3 当自由度充分大时，

分布收敛于标准正态分布

证明 还是利用构造型定义！看出它的重要性了吗？

由于

其中

，因此只需证明

，也等价于

.

，其特征函数为

，进而

的特征函数为

而

为退化分布

的特征函数，因此

.

此外也可以利用

分布的构造型定义结合弱大数定律得到

从密度函数图像中可以发现，

分布的峰值小于标准正态分布峰值，，而其“尾巴”较标准正态分布要“厚重”，因此补充给出下面的定理：

定理T4 设

,则对

，总存在

使得

分布的矩

利用构造型定义，结合正态分布及卡方分布的矩可以得到

要说明的是，只要当

时，

阶矩才存在。由于密度函数是偶函数，所以奇数阶矩为0.

特别地

可以发现，当

分布方差存在时，其比标准正态分布的方差来的大.

※

分布

构造型定义

设

且二者独立，则

的分布称为具有自由度

（或第一自由度为

，第二自由度为

）的

分布，记为

或

概率密度函数

的密度为（仅供观赏）

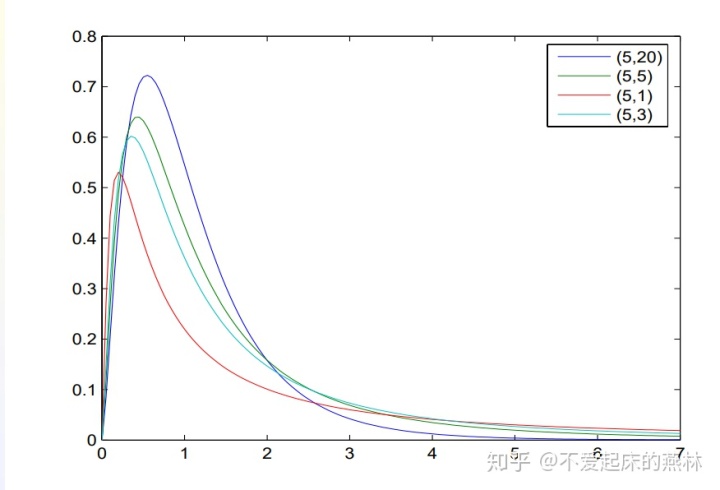
下面是密度函数的示意图

F分布密度函数

性质

倒数自由度交换

利用构造型定义即可，上下两个卡方的自由度刚好交换.

思考一下如果

，那么

服从？

根据构造型定义有

因此

定理F1

设

,

且假设

与

相互独立，设

为

的样本方差，

为

的样本方差，则

证明 还是一样，看到样本方差就要想到卡方哦

又由于来自两正态总体的样本独立，因此

下面一并介绍分布的上分位数：

之前介绍过下

分位数是使得分布函数取值为

的

值，相反，上

分位数是使得分布函数取值为

的

值，直观上看，上

分位数

使得密度函数在

右侧的积分面积为

.

下面对不同分布加以介绍

标准正态分布

记其上

分位数为

，可以通过查标准正态分布表得到它的值，并且根据标准正态分布的对称性有

.

分布

记其上

分位数为

，当

时有

分布

记其上

分位数为

，根据对称性有

，当

时

分布

记其上

分位数为

，它有个非常重要的

三变性质：

思考下如何证明呢？