
3-6 关系的性质
自反
定义3-6.1 : 设R为定义在集合X上的二元关系,如果对于每一个则称二元关系R是自反的。
例如,在实数集合上,,因为对于任意的实数,
成立;
又如平面上的全等?三角形是自反的
对称
定义3-6.2 : 设R为定义在集合上的二元关系,如果对于任意的,有
可以找到一个y,推出
,则成集合X上,关系R是对称的。
于是这样就人为地减少了y的可能性,而对称应该是对于X中全体元素而言的。
这样,有些集合上的关系,即使自反的,又是对称的。
但是其中,自反和对称也有些许不同:
- 如果自反,说明,对任意的元素,R满足”交换律”,而因为是自身对自身的关系(xRx),缺少了 对称中y的任意性
- 对称是满足自反条件的么?
- 如果说 R是对称关系,那么由于x,y的任意选取,势必会涉及到x=y的情况,如果满足了这种情况的话,对称的前件是xRy,那是否可以说明就存在xRx了呢?
- 即对称关系都满足自反,但是自反不一定能推出对称???
- 另外,对称说“每当xRy”,那么xRy是一定成立的么?
传递
定义3-6.3:设R定义在X上的二元关系,对于,每当 xRy , yRz时,就有xRz
值得一提的是,要事先成立 xRy,yRz 才可以
Ex:
反自反
定义3-6.4: R为定义在X上的二元关系,若对于每一个X中的元素x来说,都存在,那么我们说,R为反自反的
换言之,要求X中的元素, 全部 不自反,才是反自反。 不可以存在有一部分的 自反 自反 和 反自反 是分属于两个极端情况的,中间还有 “部分自反,部分不自反”的情况。 一个“不是自反”的关系,“不一定“就是”反自反“;一个不是 反自反 的关系,也同样不一定就是自反。
反对称
定义3-6.5:R为定义在X上的二元关系,若对于,那么一定有x=y
序偶属于反对称么???
换言之,若对于![]()
- 反对称和对称有包含关系,因为所谓“全等”,既是对称,又是反对称,因为我们承认了一个元素的唯一性。 所以在这种 “全等”情况下, 我们成它既是对称,又是反对称 的(x=y)
Ex:A={1,2,3},S在A上,S={<1,1>,<2,2>,<3,3>} S在A上就既是对称,又是反对称的。
- 同样的,也有既不是对称,也不是反对称 的情况。 这是因为对称关系,要求<x,y>,<y,x>同时在S中出现,如果我们在对称时,随便取出一个<y,x>但不取走全部的<y,x>,我们就可以实现两个“既不”
Ex:A={a,b,c},S在A上,S={<a,b>,<a,c>,<c,a>},那么S在A上就既不是对称的,也不是反对称的。
- 或许我们可以换言之,如果把对称关系中全部的<y,x>都取出,那么就是反对称的;
- 如果只取出部分,那么就是 既不是对称,也不是反对称的。
- 如果仅仅 x=y,那么就 既是对称,也是反对称的。
这里要注意的是,如何用矩阵/图来表示集合上的关系
3-7 复合关系和逆关系
复合
R是A到B的二元关系,S是B到C的二元关系,存在B中的一个元素y, 有<a,y>,<y,c>,则有<a,c>.
合成运算是对关系的二元运算,它能够由 两个关系生成一个新的关系。
二元运算:xx和yy——生成一个新的关系,这里的xx,yy可以任意选取,甚至可以选取另一组运算。
- 合成运算是可结合的 A---B---C
- R本身所组成的复合关系 :
复合关系也可以使用矩阵表示
其中,
0
这与矩阵的乘法相似,不过我们要注意的是,如果按照“矩阵乘法”计算出大于1的数,在关系矩阵中,我们都按照1来计算(即 非零常数皆为1)
矩阵的乘法:
矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义。一般单指矩阵乘积时,指的便是一般矩阵乘积。
1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
3、乘积C的第m行第n列的元素等于 矩阵A的第m行的元素与 矩阵B的第n列对应元素 乘积之和


除了上述的矩阵乘法以外,还有其他一些特殊的“乘积”形式被定义在矩阵上,值得注意的是,当提及“ 矩阵相乘”或者“ 矩阵乘法”的时候,并不是指代这些特殊的乘积形式,而是定义中所描述的矩阵乘法。在描述这些特殊乘积时,使用这些运算的专用名称和符号来避免表述歧义。

struct Matrix:vector<vector<int> >//使用标准容器vector做基类,需#include语句
{
Matrix(int x=0,int y=0,int z=0)//初始化,默认为0行0列空矩阵
{
assign(x,vector<int>(y,z));
}
int h_size()const//常量说明不可省,否则编译无法通过
{
return size();
}
int l_size()const
{
return empty()?0:front().size();//列数要考虑空矩阵的情况
}
Matrix pow(int k);//矩阵的k次幂,用快速幂实现,k为0时返回此矩阵的单位矩阵
};
Matrix operator*(const Matrix &m,const Matrix &n)//常量引用避免拷贝
{
if(m.l_size()!=n.h_size())return Matrix();//非法运算返回空矩阵
Matrix ans(m.h_size(),n.l_size());
for(int i=0; i!=ans.h_size(); ++i)
for(int j=0; j!=ans.l_size(); ++j)
for(int k=0; k!=m.l_size(); ++k)
ans[i][j]+=m[i][k]*n[k][j];
return ans;
}
Matrix Matrix::pow(int k)
{
if(k==0)
{
Matrix ans(h_size(),h_size());
for(int i=0; i!=ans.h_size(); ++i)
ans[i][i]=1;
return ans;
}
if(k==2)return (*this)*(*this);
if(k%2)return pow(k-1)*(*this);
return pow(k/2).pow(2);
}2020.4.2更新
逆关系
定义3-7.2 设R为X到Y的二元关系,如果将R中每一序偶的元素顺序互换,所得到的集合成为R的逆关系。记作![]()
简而言之, 是在序偶的“序”上做文章。颠倒过来的关系 父子——子父
从逆关系的定义 得出
定理3-7.1 R,R1,R2都是从A到B 的二元关系,则![]()
定理3.7-2 设T:X→Y, S:Y→Z,![]()
定理3.7-3 R为X上的二元关系,
- R是对称的,当且仅当
- R是反对称的,当且仅当
转置矩阵


3-8 关系的闭包运算
给定的关系——扩充一些序偶——得到具有某些特殊性质的新关系
定义3-8.1 设R是X上的二元关系,如果有另一个关系R'满足:
- R'是自反的 (或者对称的,可传递的。我们以自反为例叙述 闭包运算的性质)
-
- 对于任何自反的 关系R'',如果有
,则有
则称R'为R的自反闭包。
自反闭包 是包含R的 最小自反关系。对称,传递亦然。
记作:R上,
- 自反闭包——r(R)
- 对称闭包——s(R)
- 传递闭包——t(R)
- R是自反的,当且仅当r(R)=R
t(R)Warshall 有效算法
简言之:若第a列上的x,y,z行的值为1,那么就x,y,z行的数统统与第a行相加,得到一个新的矩阵,然后继续 逐列扫描。
//初始化 输入矩阵
int R[n][n] = {0};
for(int i1 = 0; i1 <= n-1; i1++)
for(int j1 = 0; j1 <= n-1; j1++)
scanf("%d",&R[i1][j1]);
//Warshall
for(int i2 = 0; i2 <= n-1; i2++)
for(int j2 = 0; j2 <= n-1; j2++)
{
if(R[j2][i2] != 0)
{
for(int k = 0; k <= n-1; k++)
R[j2][k] |= R[i2][k];
}
}
代码原文链接:https://blog.youkuaiyun.com/weixin_41934068/java/article/details/80274795
2020.4.7
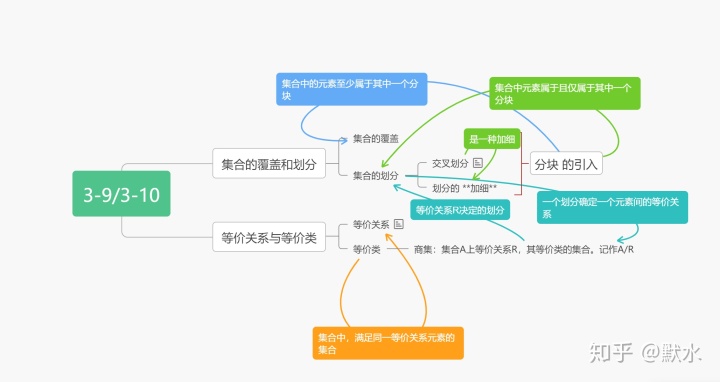
3-9 集合的划分和覆盖
定义3-9.1 分块 -->覆盖 or 划分
覆盖——A中每个元素至少属于一个分块
划分——每个元素属于且仅属于一个分块
覆盖/划分——都是全体分块构成的集合
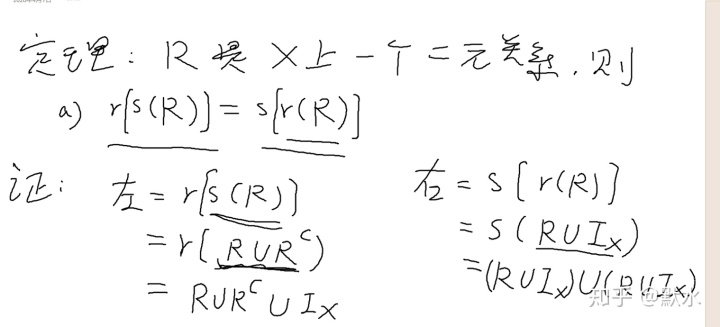






 本文详细探讨了离散数学中的关系性质,包括自反、对称、传递、反自反和反对称。对称关系并不总是自反的,但自反关系总是对称的。还介绍了复合关系、逆关系的概念,以及关系的闭包运算,如自反闭包、对称闭包和传递闭包。最后,阐述了集合的划分和覆盖的定义。
本文详细探讨了离散数学中的关系性质,包括自反、对称、传递、反自反和反对称。对称关系并不总是自反的,但自反关系总是对称的。还介绍了复合关系、逆关系的概念,以及关系的闭包运算,如自反闭包、对称闭包和传递闭包。最后,阐述了集合的划分和覆盖的定义。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








