【监督学习】第八课 树型学习方法与集成方法（Adaboost，回归树，分类树，bagging）

这节课讲的是各种树相关的学习算法或模型，以及它们是如何集成的。

树方法试图将空间分割成长方形集合，然后在这些长方形上拟合一个模型。

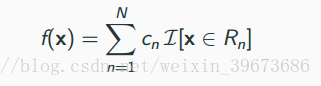
其中Rn表示一个 区域，region。也就是一个长方形。这些长方形彼此没有交集，共同构成整个空间。

I函数则表示对或错。如果x属于Rn，那么I的值为1，否则为0.

而cn代表自然选择。也就是在Rn区域中所有y的平均值。

利用单阈值，我们可以对某个属性值进行切割，将一个平面分成两个。如果不停的切分，整个空间都可以无限分割下去。

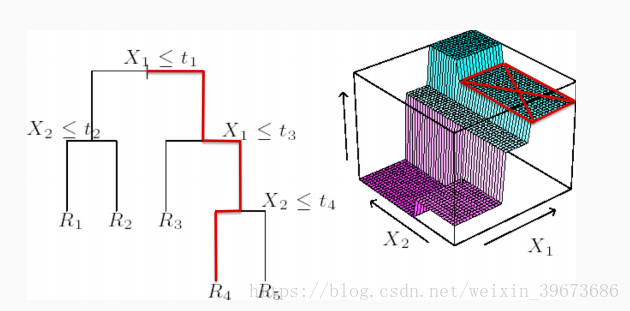
如图，有三个属性，只对其中的两个属性做切分，最后可以将整个空间分成5个区域，而R4就是红色被标记的区域。

可以看出，树方法有良好的解释性，但有过拟合的风险。

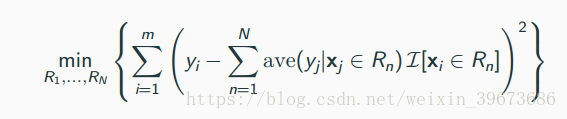
理论上说，我们需要找到N个区域让平方误差最小。但是实际上这个过程会耗费大量计算资源。于是我们用另一个启发性算法。

首先定义一个区域函数，R1表示第j个属性值小于s的 数据点x，R2表示大于。