导读
前一段时间写了一个并行计算超大图的连通分量程序,一开始在网上查找资料时,只能找到非常有限的资料。后面看了几篇论文,终于磕磕碰碰地写了出来,简单地整理了一下发个文章,一方面加深一下自己记忆,另一方面也希望能够帮助到一些在找资料的同学。
1. 连通分量
定义:无向图G的极大连通子图称为G的连通分量(Connected Component)
2. 数据准备
选用邻接矩阵来表示图,连通分量算法一般是用无向图,本次使用程序生成约13GB的无向图数据。
说一下数据生成算法思路:
数据结构是邻接矩阵,这里我们设计权重都是正值,则用0表示vi和vj之间没有链接。只需要两个循环,就可以生成n行n列的邻接矩阵。由于图太大了,且是无权图,点A到点B的权重和点B到点A的权重是一样的,无权图的邻接矩阵是关于对角线对称的,我们在生成数据的时候,把对角线的另一边的权重都赋值成0,这样可以不用维护一个邻接数组缓存。生成的过程中,权值是一个随机值,有可能生成不连通的节点,让整个图含有多个连通子图。
生成数据代码:
public class GraphGenerator {
public static void main(String[] args) throws IOException{
BufferedWriter file = new BufferedWriter(new FileWriter(new File("test.txt")));
Random random = new Random();
int vertexNum = Integer.valueOf(args[0]);
int type = Integer.valueOf(args[1]);
int maxWeight = 500;
int temp_weight = 0;
for(int i = 0; i < vertexNum; i++) { // 行数
file.write(String.valueOf(i)); // 行数
if (i%10 == 0) {
System.out.println("i="+i);
}
for(int j = 0; j < vertexNum; j++) { // 列数
if (i==j) {
temp_weight = 0;
// 当j < i 时,就不写了
}else if(j < i) {
temp_weight = 0;
// 当j > i时,随机出新的权重
}else if (j > i) {
if (type==1) {
do {
temp_weight = random.nextInt(maxWeight);
} while (temp_weight == 0);
}else if(type==2){
temp_weight = random.nextInt(2);
if (temp_weight>0) {
temp_weight = 1;
}else {
temp_weight = 0;
}
}
}
file.write("t");
file.write(String.valueOf(temp_weight));
}
file.newLine();
}
file.close();
}
}生成13.5G的部分数据:

3. 算法设计
采用标签传播算法,算法思路是:
图中的每个顶点都有一个唯一的标签,这里设定每个顶点的初始标签值为顶点的id。遍历图中的每个顶点,把顶点的标签值传播给它的邻接顶点,如果邻接顶点接收到的标签值比邻接顶点本身的标签值要小,则把邻接顶点自身的标签值替换成更小的标签值。
不断地遍历图中顶点,直到没有任何标签值发生替换,此时每个顶点中的标签值都是它所属连通子图中的最小顶点的id。最后,相同标签值的顶点是属于同一个连通子图,通过对标签值的分辨,就可以找到多个连通子图,进而找到原图的连通分量了。
步骤如下:
- 初始化:邻接矩阵转换成
vertex.id<TAB>vertex.lable<TAB>adj_vertex.id:adj_vertex.lable<TAB>.... - 标签传播算法迭代:不停地迭代,直到没有标签值发生替换
- 格式化输出:在多个子图中找出最终的连通分量
3.1 初始化
读取邻接矩阵数据,最后合并输出成每个顶点和对应的标签值、邻接顶点和邻接顶点标签值。这里会用到一个分区类,用来保证同一个key的数据会在相同的reducer中出现。
public class InitPartition extends Partitioner<LongWritable, LongWritable>{
@Override
public int getPartition(LongWritable key, LongWritable value, int reducerNum) {
long result = key.get() % reducerNum;
return (int)result;
}
}3.1.1 Mapper设计
读取邻接矩阵,输入的格式的例子如下:
- 输入0 0 1 0,
各个数字从左到右表示,
第一个0:第0行数据,表示这行数据从第二列往后是顶点0和所有顶点的权重;
第二个0:顶点0和顶点0的权重是0,表示不连接;
第三个1:顶点0和顶点1的权重是1,相互连接;
第四个0:顶点0和顶点2的权重是0,不连接。
- 输出邻接边:
vertex.id<TAB>vertex.id
上面的输入例子最后Mapper输出,0 1
如果一个顶点没有任何的邻接顶点,则输出标签值为-1,让后续的流程不对该顶点处理。
public class InitMapper extends Mapper<LongWritable, Text, LongWritable, LongWritable>{
@Override
protected void map(LongWritable key, Text value, Mapper<LongWritable, Text, LongWritable, LongWritable>.Context context)
throws IOException, InterruptedException {
String valueStr = value.toString().trim();
String[] splits = valueStr.split("t");
long vertexArr = Long.valueOf(splits[0]);
long vertexCol = -1;
long adj_vertex_num = 0;
for(String weightStr : splits) {
if (vertexCol >= 0) {
long weight = Long.valueOf(weightStr);
if(weight != 0 && weight != Long.MAX_VALUE) {
adj_vertex_num++;
context.write(new LongWritable(vertexArr), new LongWritable(vertexCol));
context.write(new LongWritable(vertexCol), new LongWritable(vertexArr));
}
}
vertexCol++;
}
if (adj_vertex_num == 0) {
context.write(new LongWritable(vertexArr), new LongWritable(-1));
}
}
}3.1.2 Reducer设计
输出:vertex.id<TAB>vertex.lable<TAB>adj.id:adj.lable<TAB>adj.id:adj.lable...
public class InitReducer extends Reducer<LongWritable, LongWritable, LongWritable, Text>{
StringBuilder sb = new StringBuilder();
@Override
protected void reduce(LongWritable key, Iterable<LongWritable> values,
Reducer<LongWritable, LongWritable, LongWritable, Text>.Context context) throws IOException, InterruptedException {
sb.delete(0, sb.length());
Text outValue = new Text();
long adj_num = 0;
sb.append(key.get());
for(LongWritable value : values) {
long value_long = value.get();
if (value_long >= 0) {
sb.append("t");
sb.append(value.get());
sb.append(":");
sb.append(value.get());
adj_num++;
}
}
// 这个顶点 没有任何邻接列表
if (adj_num == 0) {
context.write(key, new Text("-1"));
}else {
outValue.set(sb.toString());
context.write(key, outValue);
}
}
}3.2 标签传播算法迭代
这里也用到了分区函数,和初始化的分区函数一样。同时,还使用了hadoop的全局计数器来记录标签值替换的次数。
3.2.1 Mapper设计
输入:vertex.id<TAB>vertex.lable<TAB>adj.id:adj.lable<TAB>adj.id:adj.lable
首先在遍历自己和邻接顶点的标签值,找到其中最小的标签值。一一比较各个顶点的标签值和最小标签值的大小,如果比最小标签值小,替换标签值。发生标签替换的同时,map要额外输出一对数据: vertex.id<TAB>vertex.min_lable,这样在reducer中就能收到对应vertex已经发生了标签替换,会更新自己的标签值。
public class PropagationMapper extends Mapper<LongWritable, Text, LongWritable, Text>{
public static enum CCLableChangeCounter{
totalChange //计数作用 统计各个顶点改变的次数
}
StringBuilder sb = new StringBuilder();
@Override
protected void map(LongWritable key, Text value, Mapper<LongWritable, Text, LongWritable, Text>.Context context)
throws IOException, InterruptedException {
LongWritable outKey = new LongWritable();
Text outValue = new Text();
sb.delete(0, sb.length());
String valueStr = value.toString().trim();
String[] splits = valueStr.split("t");
String vertexArrStr = splits[0];
long vertexArr = Long.valueOf(vertexArrStr);
outKey.set(vertexArr);
String vertexArrLableStr = splits[1];
long vertexArrLable = Long.valueOf(vertexArrLableStr);
// 孤独的顶点,没有邻接列表,不处理
if(vertexArrLable == -1) {
context.write(outKey, new Text("-1"));
return;
}
long min_lable = vertexArrLable;
// 找到最小的标签
for(int i = 2; i < splits.length; i++) {
String adj_id_lable = splits[i];
String[] adj_splits = adj_id_lable.split(":");
// long adj_id = Long.valueOf(adj_splits[0]);
long adj_lable = Long.valueOf(adj_splits[1]);
if (min_lable > adj_lable) {
min_lable = adj_lable;
}
}
sb.append(min_lable);
for(int i = 2; i < splits.length; i++) {
String adj_id_lable = splits[i];
String[] adj_splits = adj_id_lable.split(":");
long adj_id = Long.valueOf(adj_splits[0]);
long adj_lable = Long.valueOf(adj_splits[1]);
sb.append("t");
sb.append(adj_id);
sb.append(":");
if(min_lable < adj_lable) {
adj_lable = min_lable;
context.getCounter(CCLableChangeCounter.totalChange).increment(1);
// 标签改变,需要告知顶点,所以要单独输出一个
context.write(new LongWritable(adj_id), new Text(String.valueOf(adj_lable)));
}
sb.append(adj_lable);
}
outValue.set(sb.toString());
context.write(outKey, outValue);
}
}3.2.2 Reducer设计
输入的是:vertex.id<TAB>vertex.lable<TAB>adj.id:adj.lable<TAB>adj.id:adj.lable
或者是 vertex.id<TAB>vertex.lable
reducer要做的是,检测vertex.id有没有发生标签值替换,有的话,这里要更新对应的标签值。
public class PropagationReducer extends Reducer<LongWritable, Text, LongWritable, Text>{
StringBuilder sb = new StringBuilder();
@Override
protected void reduce(LongWritable key, Iterable<Text> values,
Reducer<LongWritable, Text, LongWritable, Text>.Context context) throws IOException, InterruptedException {
sb.delete(0, sb.length());
String vertex_to_lable = "";
long min_lable = Long.MAX_VALUE;
for(Text value: values) {
String vString = value.toString().trim();
String[] splits = vString.split("t");
long temp_lable = Long.valueOf(splits[0]);
if (min_lable > temp_lable) {
min_lable = temp_lable;
}
if (splits.length >= 2) {
vertex_to_lable = value.toString();
}
}
// 孤独的顶点
if (min_lable == -1) {
context.write(key, new Text("-1"));
return;
}
String[] splits = vertex_to_lable.split("t", 2);
sb.append(min_lable);
sb.append("t");
sb.append(splits[1]);
context.write(key, new Text(sb.toString()));
}3.3 格式化输出
迭代完成后,我们就能根据各个顶点的标签值来分类了。这里也用了分区函数,和初始化过程中使用的是一样的。
简单地根据标签值聚合到reducer,然后比较哪个子图的顶点数最大即可,这里因为要涉及到比较各个子图的顶点数大小,为了方便,设定reducer数量只有一个。
3.3.1 Mapper设计
输入的是:vertex.id<TAB>vertex.lable<TAB>adj.id:adj.lable<TAB>adj.id:adj.lable
输出vertex.lable<TAB>vertex.id即可。
public class TerminationMapper extends Mapper<LongWritable, Text, LongWritable, LongWritable>{
@Override
protected void map(LongWritable key, Text value,
Mapper<LongWritable, Text, LongWritable, LongWritable>.Context context)
throws IOException, InterruptedException {
String valueStr = value.toString().trim();
String[] splits = valueStr.split("t", 3);
String vertexStr = splits[0];
String lableStr = splits[1];
long vertex = Long.valueOf(vertexStr);
long lable = Long.valueOf(lableStr);
context.write(new LongWritable(lable), new LongWritable(vertex));
}
}3.3.2 Reducer设计
最后所有相同标签值的顶点都聚合到了一次reduce处理中,不同标签值的个数即是连通子图的个数。遍历所有的标签值,然后找到顶点数量最多的连通子图,在cleanup函数中输出即可。
public class TerminationReducer extends Reducer<LongWritable, LongWritable, NullWritable, Text>{
StringBuilder sb = new StringBuilder();
Vector<String> outValueVec = new Vector<String>();
long max_vertex_size = 0;
@Override
protected void reduce(LongWritable key, Iterable<LongWritable> values,
Reducer<LongWritable, LongWritable, NullWritable, Text>.Context context)
throws IOException, InterruptedException {
long vertex_size = 0;
sb.delete(0, sb.length());
for(LongWritable value: values) {
vertex_size++;
long vertex = value.get();
sb.append(vertex);
sb.append(",");
}
if (max_vertex_size < vertex_size) {
max_vertex_size = vertex_size;
outValueVec.clear();
outValueVec.add(sb.toString());
}else if (max_vertex_size == vertex_size) {
outValueVec.add(sb.toString());
}
}
@Override
protected void cleanup(Reducer<LongWritable, LongWritable, NullWritable, Text>.Context context)
throws IOException, InterruptedException {
for(String string: outValueVec) {
context.write(NullWritable.get(), new Text(string));
}
}
}3.4 执行
执行时间较久,挂到后台去执行。

执行时间:一共迭代了3次,共2小时13分钟
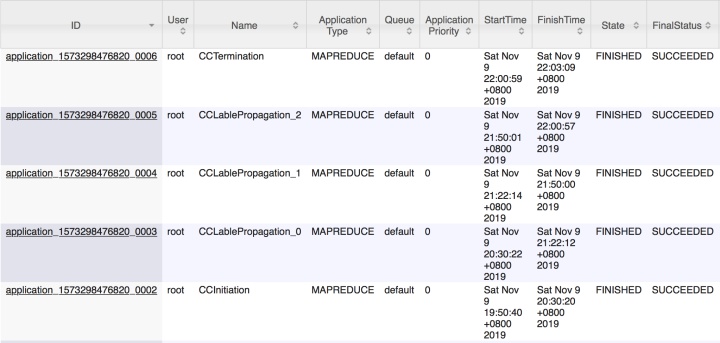
执行结果(输出连通分量的顶点id):























 4905
4905

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








