
周末,抓紧时间学习利用python写排序算法。
在第1回,笔者介绍了Anaconda安装Python 3.7的方法,现在直接打开Anaconda中的Spyder来写代码吧。
小黄鹂:第1回:Python的安装与使用(1)zhuanlan.zhihu.com
排序算法是计算机算法的基础内容,这方面的文章和介绍也是不计其数。读者可自行参考以下文章了解常用的排序方法及其时间复杂度:九种排序算法的可视化及比较
有关复杂度的概念可以参考:十分钟搞定时间复杂度(算法的时间复杂度)
在Python中,可以通过简单的.sort() 函数来完成对数列的升序或降序排序。格式如下:
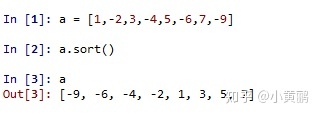
有关.sort()的具体用法请参考:Python List sort()方法
今天我们主要是想通过自己写的一个递归排序法,来讲解python的代码编写的基本方法。
首先介绍一下递归:程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
递归排序所采用的高速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要Ο(n log n)次比较。高速排序通常明显比其它Ο(n log n) 算法更快,由于它的内部循环(inner loop)能够在大部分的架构上很有效率地被实现出来。高速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
算法步骤为:
1. 从数列中挑出一个元素,称为 “基准”(pivot)。
2. 第一次排序数列,全部元素比基准值小的摆放在基准前面。全部元素比基准值大的摆在基准的后面(相同的数能够到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
3. 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,可是这个算法总会退出。由于在每次的迭代(iteration)中。它至少会把一个元素摆到它最后的位置去。
Python代码如下:
# -*- coding: utf-8 -*- # 用utf-8的编码方式
import numpy as np # 加入np,为主函数中产生随机数
# =============================================================================
# 定义递归函数
# =============================================================================
def QuickSort(disorder, statpoi, endpoi): # 定义起点和终点
if endpoi - statpoi > 0: # 定义递归运行条件
tmpleft = [] # 定义list用来存放不大于的值
tmpright = [] # 定义list用来存放大于的值
tmp_val = disorder[statpoi] # 选定起始点作为比较基准
for i in range(statpoi+1, endpoi): # 选定比较的范围
if disorder[i] <= tmp_val: # 比较的条件
tmpleft.append(disorder[i]) # 比tmp_val小,放在左边
else:
tmpright.append(disorder[i]) # 比tmp_val大,放在右边
midpoi = statpoi+len(tmpleft) # 得到基准点在比较、移动后的坐标
tmpleft.append(tmp_val) # 将tmpleft临时作为整个数组的存放位置,加入基准点
for j in tmpright: # 将tmpleft临时作为整个数组的存放位置,加入tmpright的值
tmpleft.append(j)
for k in range(len(tmpleft)): # 将临时值存放入原数组中
disorder[k+statpoi] = tmpleft[k]
print(disorder)
QuickSort(disorder, statpoi, midpoi) # 递归,为左边排序
QuickSort(disorder, midpoi+1, endpoi) # 递归,为右边排序
else:
return disorder
# =============================================================================
# 主体语句
# =============================================================================
a = np.random.randint(-100, 100, [1,15])[0] # 需要排序的阵列,按升序排列
print(a) # 打印原始数组
QuickSort(a,0,len(a)) # 调用函数该代码主要包含以下几个部分:
- 函数体前:声明采用utf-8编码方式,目的是兼容中文,不出现乱码。同时在代码中加入了一个常用库:numpy,用来随机数生成的阵列。numpy是一个常用的数学运算库,更多请参考:一篇文章掌握Numpy的基本用法。
- 函数体:函数体的定义请参考廖雪峰老师的网站:

递归函数的具体声明和使用在函数体中已经通过注释的方法写出,即代码中的“#”号以后的部分。递归过程的一个难点是递归的参数该如何确定。请读者自己在python中尝试读懂每一步的作用。Tips: 可以在适当地方加入print行,来获取每一行参数的变化结果。
3. 函数调用:最后利用np库产生的随机数阵列来产生一个随机数数组。产生随机数的方法可参考:Python 生成 -1~1 之间的随机数矩阵方法。本文中产生了从-100到100之间的1行15列随机整数。最后代码的运行结果如下:
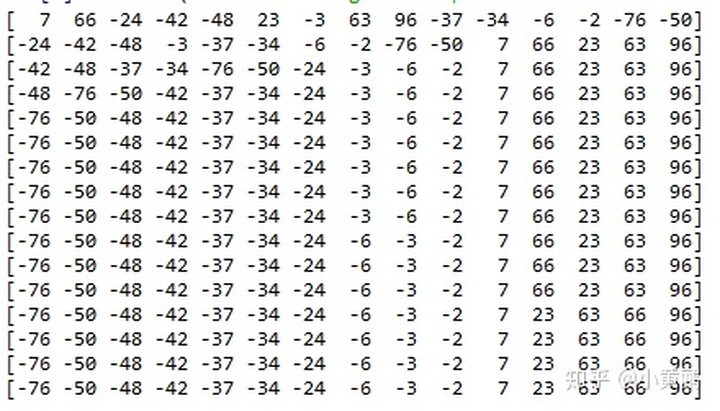
请读者自行分析在排序过程中的分区、排序和迭代过程。也可以在函数中增加降序功能来做练习。如果有问题,欢迎留言讨论。
好了,今天的内容就到这里。祝大家工作精神百倍,效率天天百分百。























 800
800

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








