吴恩达机器学习 笔记整理 Chapter2 单变量线性回归

Main Procedure

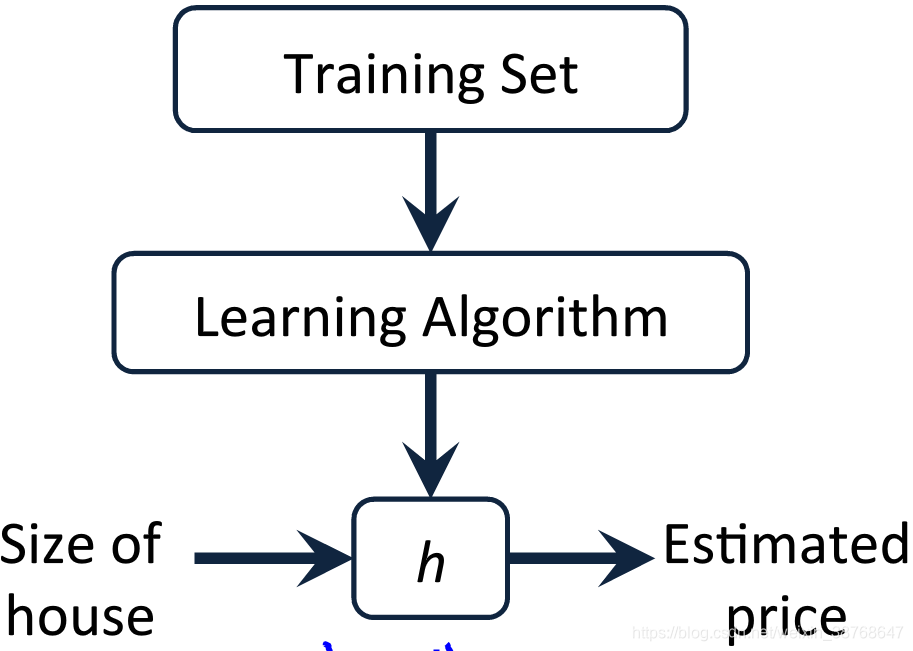
hypothesis

a function that maps input to output

Univariate linear regression

$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

Cost function

Idea

Choose $\theta$ so that $h_{\theta }(x)$ is close to y for our training examples (x,y).
To fit the function to training data => To minimized the cost function
To minimize the square difference between the hypothesis and the actual value

Cost function for Univariate linear regression

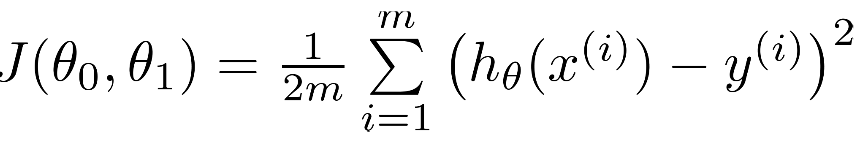
Gradient Descent

An algorithm for minimizing the cost function.

Intuition: contour plot for $J(\theta )$

To minimize as quickly as possible

Outline

1. Start with some ${\theta }_0$, ${\theta }_1$ (Random Initialize)
2. Keep changing ${\theta }_0$, ${\theta }_1$ to reduce $J({\theta }_0,{\theta }_1)$ until end up at minimum (Although sensitive of local mini, usually get global mini)

Algorithm: To minimize as quickly as possible

Repeat util convergence{

}
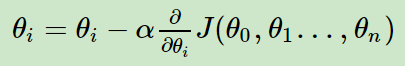
NOTE: All the parameter ${\theta }_i$ should be update simultaneously.

$\alpha$: learning rate

Need to choose carefully.

• Too small: gradient descent can be slow
• Too large: it can be overshoot the minimum. It may be fail to converge, or even diverge

Gradient descent can converge to a local minimum, even with learning rate a fixed
As we approach a local minimum, gradient descent will automatically take smaller steps(because the partial derivative will become smaller). So there is no need to decrease $\alpha$ overtime.

Gradient Descent for Univariate Linear Regression

Problem: susceptible to local optima
It’s okay because the cost function for linear regression is a convex function

Batch Gradient Descent

Each step uses all the training examples.