4.1 群的概念
群的定义
给定一个集合G={a,b,c,…}和集合G上的二元运算∙\bullet∙,并且满足以下4个条件:
- 封闭性
- 满足结合律
- 存在一个单位元素e
- 对于任意元素a都存在逆元素
称集合G在运算∙\bullet∙之下是一个群,也称G是一个群。元素a∙ba\bullet ba∙b简记为ab。
##子群的定义
设G是群,H是G的子集,若H在G的原来定义的运算下也构成群,则称H为群G的子群。
群的基本性质
- 群的单位元是唯一的
- ab=ac => b=c,ba=ca => b=c
- G中每一个元素的逆元素是唯一的
4.2 置换群
##置换的定义
有限集合S到自身的一一对应(替换)称为S上的一个置换。

置换群的定义
n个文字有n!个置换,这n!个置换一定构成一个群,称为n个文字的对称群,记作Sn;Sn的任一子群称为置换群;
#4.3 循环
【定理】任何一个置换都可以表示成若干不相交的循环的乘积。
【例】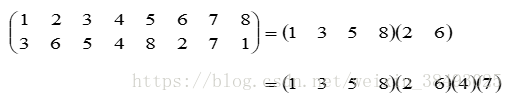
4.4 贝恩赛德引理
共轭类

【例】
文字k的k不动置换类
设G是1,2,…,n的置换群,当然G是Sn的一个子群,若k是1到n中的某个文字,G中使文字k保持不变的置换全体,叫做G中使k保持不动的置换类,或简称k不动置换类,记以Zk 。
【例】

【定理】置换群G中任意文字k的不动置换类Zk一定是G的一个子群。
【例】G={e,(12),(34),(12)(34)}
- 在群G作用下1能变为2,2能变为1,3能变为4,4能变为3.
- 1与2属于同一类,3和4属于另一类
等价类:在群G的作用下能够与文字k相互转化的文字我们称为同一类,这样的类我们称作是一个等价类,记为Ek 。
【定理】|Ek||Zk|=|G|,k=1,2,…,n
- 例如G={e,(12),(34),(12)(34)},|G|=4
- 文字1的等价类为:E1={1,2},|E1|=2
- 使1不动置换类为:Z1={e,(34)},|Z1|=2
【推论】若文字i,j属于同一个等价类,则|Zi|=|Zj|
1阶循环的个数及记法

贝恩塞特(Burnside)引理

【例】
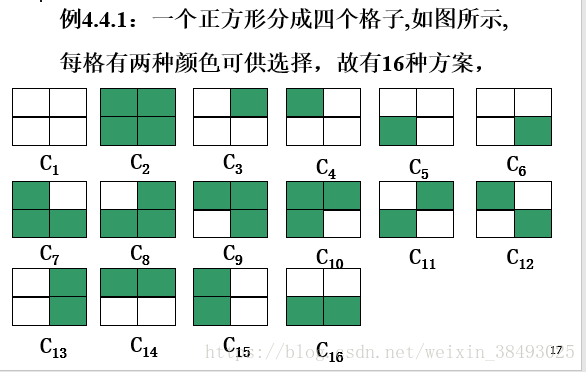

#4.5 波利亚定理

- 波利亚Polya定理中的 G‾\overline GG群是作用在__n个对象__上的置换群
- 贝恩赛德Burnside定理中的G群是在这n个对象上用m种颜色进行染色后__mnm^nmnn个染色方案__集合上的置换群
- 两个置换群是在同样的变化下得到的:∣G∣=∣G‾∣|G|=|\overline G|∣G∣=∣G∣
- c1(ai)=mc(a‾i)c_1(a_i)=m^{c(\overline a_i)}c1(ai)=mc(ai)
【例】
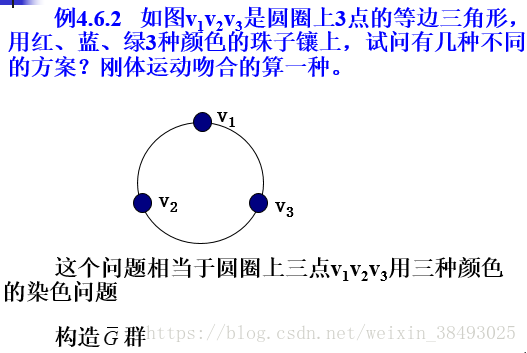 =
=
























 1134
1134

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








