组合数学第二章复习

#2.1 递推关系
对于数列a1,a2,…,an,…,除了前面的若干数外,其余各项an与它前面的若干个数关联起来的方程叫做递推关系。
在求解递推关系时，前面必须知道若干个数，这若干个已知的数称为初始条件，或边界条件。

#2.2 母函数
对于序列a0,a1,a2,… 构造函数：G(x)= a0+a1x+a2x2+… ,称函数G(x)是序列a0,a1,a2,…的母函数。

【例】有红球两个，白球、黄球各一个，试求有多少种不同的组合方案，假设两个红球没有区别。
第一种解法：组合方法

• 一个都不选：1种方案
• 选1个球：3种方案
• 选2个球：4种方案
• 选3个球：3种方案
• 选4个球：1种方案
• 共1+3+4+3+1=12种组合方案

第二种解法：母函数法

• 设r，w，y分别代表红球，白球，黄球
• 单独红球的组合方式为1，1，1，构造函数：1+r+r2
• 单独白球与单独黄球的组合方式分别为： 1,1和 1,1，分别构造函数1+w和1+y
• (1+r+r2) (1+w)(1+y)，把r,w,y都用x来表示，可得
• (1+x+x2)(1+x)(1+x)=$1+3x+4x^2+3x^3+x^4$
• 系数相加，共1+3+4+3+1=12种方案

##几个基本的母函数

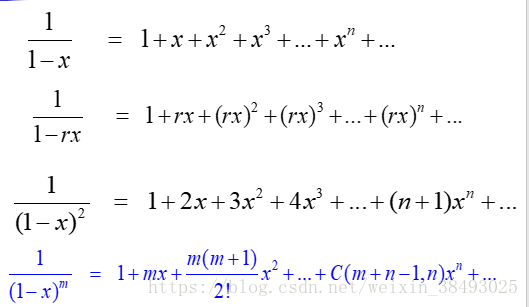
#2.3 母函数求解递推关系
【例】已知边界条件$h_0=0,h_1=1$，用母函数求解递推关系$h_n=2h_{n-1}+1$

• 假设$h_1,h_2,...,h_n$的母函数为$G(x)=h_0+h_{1}x+h_2{x}^2+...$

• 利用递推关系得，$G(x)=\frac{x}{(1-x)(1-2x)}=\frac{A}{1-x}+\frac{B}{1-2x}=A(1+x+x^2+...)+B(1+2x+2^2{x}^2+...)$

• 第n项是$A+B{2}^n$，代入边界条件$h_0=0,h_1=1$，解得A=-1，B=1

• 答案：$h_n=-1+2^n$
  #2.5 母函数的性质
  
  
  
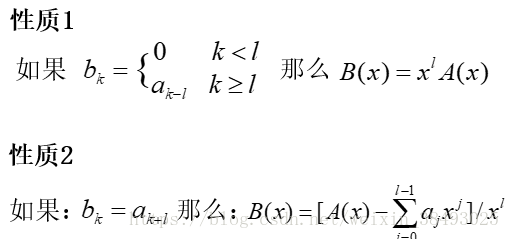
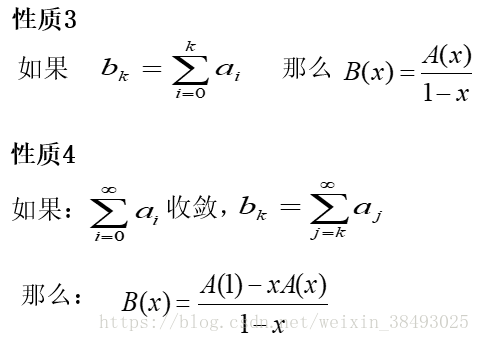
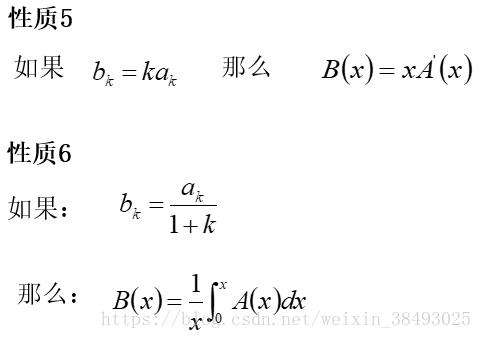
  #2.6 线性常系数齐次递推关系
  ##二阶线性常系数齐次递推关系总结
  $a_n+b{a}_{n-1}+c{a}_{n-2}=0,c̸=0$
  针对特征方程$x^2+bx+c=0$的根的情况有：

• 两个不同的实根：$a_n=A(r_1{)}^n+B(r_2{)}^n$

• 一对共轭的复根：$a_n=k_1{\rho }^{n}cos(n\theta )+k_2{\rho }^{n}sin(n\theta )$

• 两个相同的实根：$a_n=(h+kn)r^n$

【例】




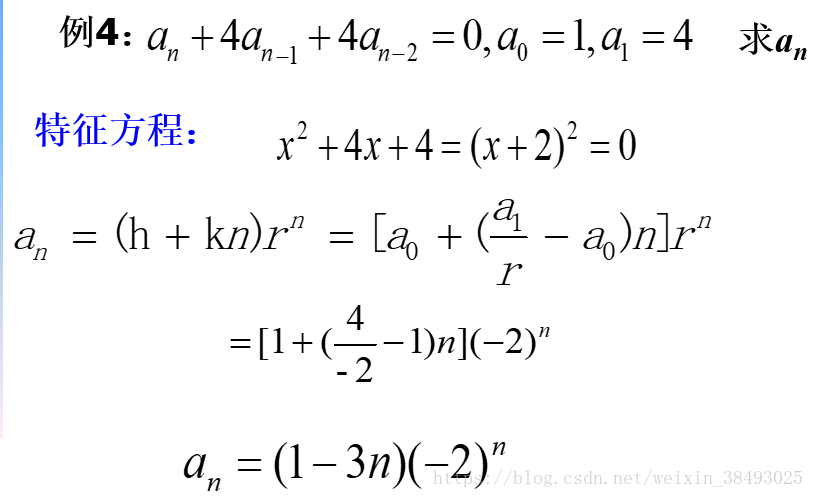
##K阶线性常系数齐次递推关系总结
$a_n+c_1{a}_{n-1}+c_2{a}_{n-2}+...+c_k{a}_{n-k}=0$
针对特征方程$x^k+c_1{x}^{k-1}+...+c_k=0$的根的情况有：

• k个不同的实根：$a_n=A_1(r_1{)}^n+A_2(r_2{)}^n+...+A_k(r_k{)}^n$
• h重根：$a_n=(k_1+k_{2}n+...+k_h{n}^{h-1})r^n$
• $h_i$是$r_i$的重根数：$a_n=(A_0+A_{1}n+...+A_{h_1}{n}^{h_1-1})r_1^n+(B_0+B_{1}n+...+B_{h_2}{n}^{h_2-1})r_2^n+...+(T_0+T_{1}n+...+T_{h_s}{n}^{h_s-1})r_s^n$

【例】


#2.7 关于线性常系数非齐次递推关系

$a_n+c_1{a}_{n-1}+c_2{a}_{n-2}+...+c_k{a}_{n-k}=b_n$

• 若$c_k̸=0$,称为k阶线性递推关系
• 若$c_1,c_2,\dots ,c_k$都是常数，则称为k阶线性常系数递推关系
• 若$b_n=0$，则称为是齐次的，否则为非齐次的。

【定理】若${\alpha }_n$ 是线性常系数非齐次递推关系的某个特解，则这个线性常系数非齐次递推关系的一般解有如下形式：
$ a_n$(非齐次的一般解)=$ α_n$ (非齐次的某个特解)+$ β_n$ (对应的齐次的一般解)
##二阶线性常系数非齐次递推关系
$a_n+c_1{a}_{n-1}+c_2{a}_{n-2}=C(n),C(n)=h{r}^n$，h是常数，r是非零整数。

• 猜解法：设$a_n=k{r}^n$
• 将非齐次递推关系化为更高阶齐次递推关系，通过比较推测出递推关系的特解

【定理】对于如下非齐次递推关系：
$$a_n+c_1{a}_{n-1}+c_2{a}_{n-2}+...+c_k{a}_{n-k}=r^{n}h(n)$$

h(n) 是n的p次多项式，线性齐次递推关系的特征方程为：
$$C(x)=x^k+c_1{x}^{k-1}+...+c_k$$

• 若r是C(x)的m重根，则递推关系的特解为如下形式：$$r^n(k_0{n}^m+k_1{n}^{m+1}+...+k_p{n}^{m+p})$$
• 若r不是C(x)=0的根，则特解是上式m=0时的形式