VINS初始化

         系统的初始化主要恢复出尺度、重力、速度以及IMU的bias.因为视觉(SFM)在初始化的过程中有着较好的表现，所以在初始化的过程中主要以SFM为主，然后将IMU的预积分结果与其对齐，即可得到较好的初始化结果。
    系统的初始化主要包括三个环节：求取相机与IMU之间的相对旋转、相机初始化(局部滑窗内的SFM，包括没有尺度的BA)、IMU与视觉的对齐(IMU预积分中的 α等和相机的translation)。

          纯视觉初始化，首先构建一个滑动窗口，包含一组数据帧。论文中提及使用的是对极几何模型的5点法求解单目相机的相对变换，包括相对旋转和无尺度信息的位移。其实基本上每个单目模型都是使用对极几何在初始化中求解两帧的相对变换，这里需要注意的是旋转是具有尺度不变性的（其实就是单位旋转，不会有尺度信息，你仔细想想是不是？）。然后三角化得到相应的3d点坐标，有这些3d点和滑动窗口中其他的帧的2d点就可以进行PNP求解获得滑动窗口中的所有的位姿和特征点3d坐标，至此，纯视觉初始化就完成了。

       一    相对旋转部分

         相机部分通过本质矩阵恢复出,IMU部分通过预积分得到的旋转矩阵,

      这两个测量满足：

                      (个人理解是左侧是R bk+1到 ck+1的转换,右侧是R bk到 ck的)

     

        

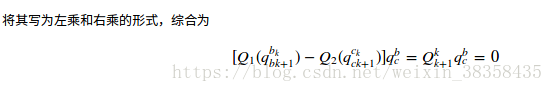
 然后多组数据获得一个方程组:

      

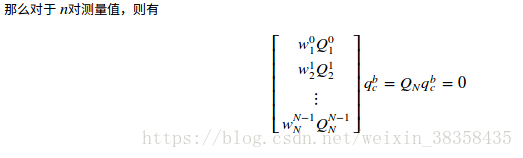
  可以获得解 .

求解过程中,涉及到w

         

 

       二   视觉与IMU对齐

           （1）      陀螺仪偏置标定

                 通过两种测量:陀螺仪的预积分和跟视觉的SFM计算出的旋转之间的误差做最小二乘,得到陀螺仪的偏置(忽略噪声的影响).

            即:

                  

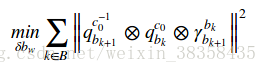
           其中:

                  

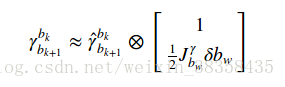
           两种旋转测量几乎相等:

                     

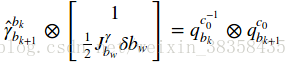
           移项得:

                    

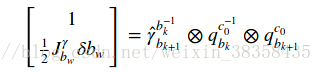
            取虚部,在进行最小二乘求解,即可得到 δbw:

                    

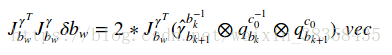
          注意这个地方得到的只是Bias的变化量，需要在滑窗内累加得到Bias的准确值.(这句话待理解)

         算出陀螺仪的偏移以后，对于每一幅图像，利用缓存的每一个IMU数据，重新计算这一段时间的每帧图像对应的预积分，雅克比矩阵和协方差矩阵。

          (2)       初始化速度、重力向量 g和尺度因子

               在这个步骤中,要估计系统的速度、重力向量以及尺度因子。所以系统的状态量可以写为:

                   

     上面的状态量都是在 c0 相机坐标系下.

              预积分的测量:

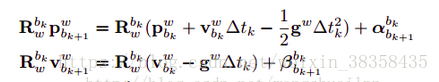                                    (1)

           前面已经得到了IMU相对于相机的旋转,假设IMU到相机的平移量(这个等看完代码再补充.不太理解的地方),那么可以很容易地将相机坐标系下的位姿转换到IMU坐标系下:

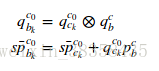                                    (2)

              由(1)公式转到c0坐标系下可得:

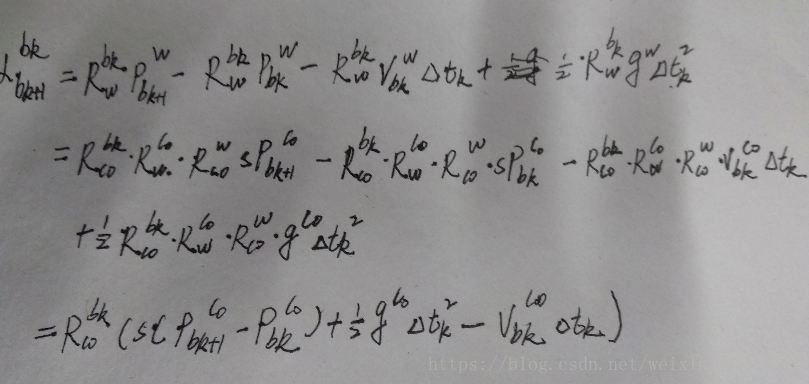                 (3)

              由(2)公式可得:

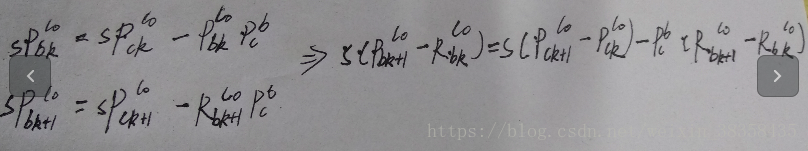              (4)

               将(4)代入到(3)可得:

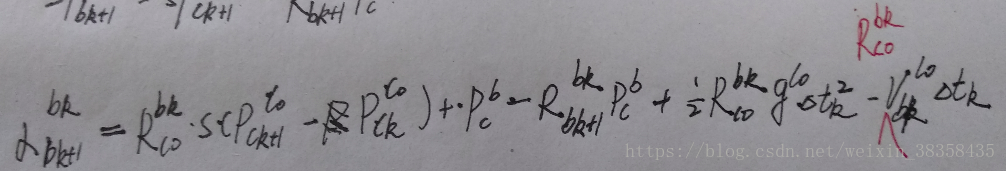                    (5)

             同理可得:

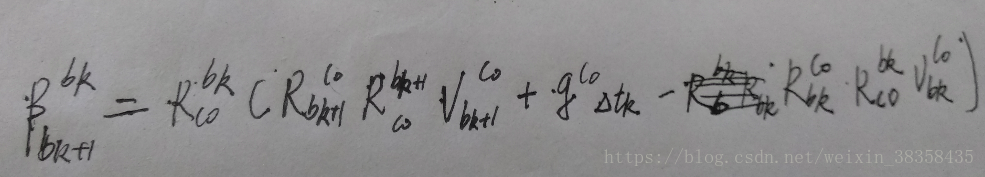                     (6)

            将(5)(6)公式移项可得:

             

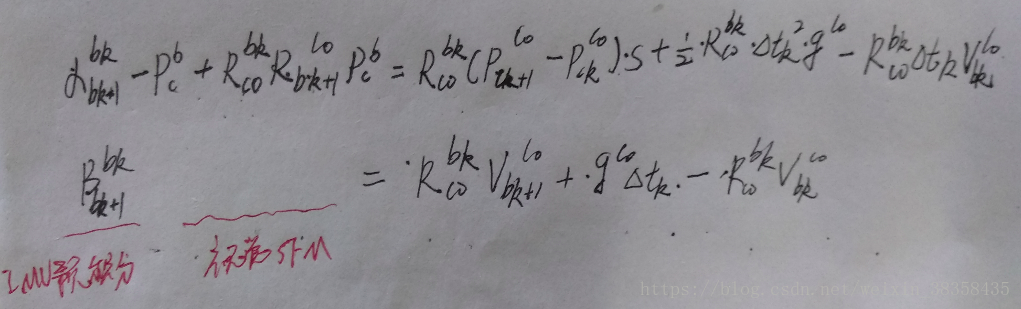
             然后写成矩阵形式:

               

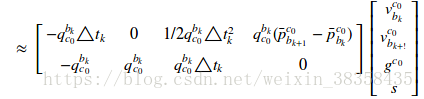
          稍加转换就是论文中的形式啦:

             

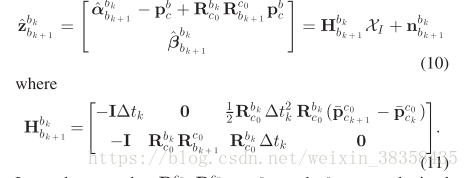
           最后求解最小二乘问题:

          

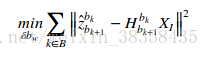
       这个最小二乘的问题是:每一帧对下一帧的IMU预测的误差与视觉SFM的误差的和

     

           (3)重力优化

            

           

       参考:

            wangshuailpp的博客-初始化部分

            VINS-Mono代码分析总结

            VINS-mono详细解读