入出栈序列的种数—递归及卡特兰数（Catalan）实现

最新推荐文章于 2022-09-27 22:23:29 发布

原创最新推荐文章于 2022-09-27 22:23:29 发布 · 2.1k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#卡特兰数 #进出栈序列的种数 #递归

递归同时被 2 个专栏收录

3 篇文章

订阅专栏

算法公式

1 篇文章

订阅专栏

本文探讨了给定元素依次进栈时所有可能的出栈序列数量问题，并给出了递归算法及Catalan数的公式，通过实例展示了如何计算不同数量元素的所有可能出栈序列。

问题描述：

上学期数据结构课讲栈的时候，老师曾出过这样一个问题，将1,2,3这三个数依次进栈，问出栈的序列有多少种？嘻嘻，大家不妨先在草稿纸上先写一下所能想到的序列，看来大家都很聪明，一共是有5种，即123、132、213、231、321。

解题思路：

首先想到的是用递归实现，一共有三种操作 ①栈为空时，必须入栈而不能出栈 ②入栈 ③出栈这里要注意的是，当全部元素入栈后，出栈序列其实就已经定了

递归代码如下：

#include<iostream>
using namespace std;
int stack(int n,int m){  //n是准备入栈的个数  m是在栈中的个数 
	if(n==0)return 1;   //全部元素都入栈了 出栈序列也就决定了 返回1种结果 
	if(m==0)return stack(n-1,1);  //栈为空 必须入栈 
	return stack(n-1,m+1)+stack(n,m-1);  //入栈 和 出栈 
}
int main(){
	for(int i=1;i<=10;i++){
		printf("1~%d依次进栈的出栈序列有:%d种\n",i,stack(i,0));
	}
	return 0;
}

输出结果如下：

1~1依次进栈的出栈序列有:1种
1~2依次进栈的出栈序列有:2种
1~3依次进栈的出栈序列有:5种
1~4依次进栈的出栈序列有:14种
1~5依次进栈的出栈序列有:42种
1~6依次进栈的出栈序列有:132种
1~7依次进栈的出栈序列有:429种
1~8依次进栈的出栈序列有:1430种
1~9依次进栈的出栈序列有:4862种
1~10依次进栈的出栈序列有:16796种

这种递归的效果如下图（以1、2、3入栈为例）：

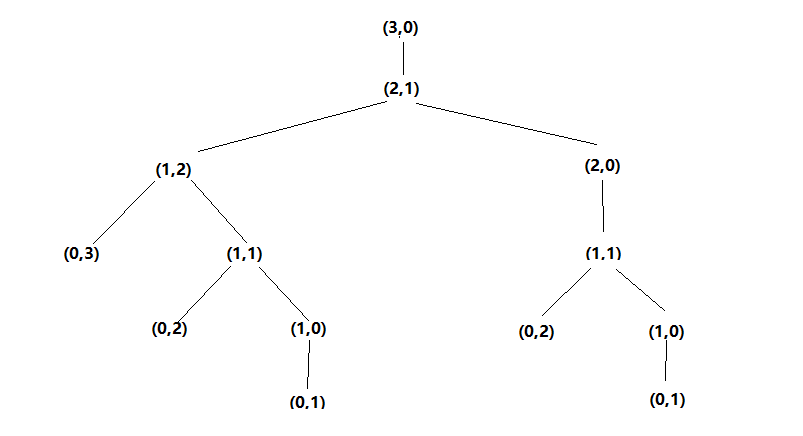
其实这道题是有公式的，叫Catalan数：是组合数学中一个常出现在各种计数问题中出现的数列。其递归式如下：

h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (其中n>=2，h(0) = h(1) = 1)

公式推导参考链接：https://blog.youkuaiyun.com/zyearn/article/details/7758716

根据递归式，写出相应的算法

#include<iostream>
using namespace std;
int main(){
	int h[1000]={0};
	h[0]=h[1]=1;  //这里假设h[0]也等于1 
	for(int i=2;i<=10;i++){
		for(int j=0;j<i;j++){
			h[i]+=h[j]*h[i-1-j];
		}
	} 
	for(int i=1;i<=10;i++)printf("1~%d依次进栈的出栈序列有:%d种\n",i,h[i]);
	return 0;
}

当然卡特兰树还有其他应用领域：

具体参考相应链接：https://blog.youkuaiyun.com/wuzhekai1985/article/details/6764858