网络流及建模专题(上)

前言

不断更新中……
这几天新坑填不下去了，回来回顾一些经典的模型套路，先拿网络流开刀，窃以为洛谷这几道网络流的题目还是非常具有代表性的，涵盖了网络流调整、多解计数、最小割、最大权闭合子图问题。
还涵盖了图论（二分图）中的一些结论和：最小不相交路径覆盖、最小可相交路径覆盖、二分图最大点权独立集、二分图最小点权覆盖集等问题，这里将简略介绍一下。

本专题包含六道题：P2765、P2764、P2763、P2766、P2774、P2805

P2765 网络流调整技巧
P2763 二分图多重匹配问题
P2764 最小不相交路径覆盖、最小可相交路径覆盖
P2766 一类dp计数问题、最多不相交路径
P2774 二分图最大点权独立集、二分图最小点权覆盖集
P2805 最大权闭合子图

前提

• 知道网络流的基本用法。
• 知道最大流最小割定理。
• 知道二分图的定义。
• 有一个稳定好用的Dinic求网络流的板子。

---

P2765 魔术球问题

前言

这道题应该可以通过贪心的方法过，不过既然放在了网络流专题里面，我们就认真的用网络流试一试并总结一下经验。

题解

添加一个小球相当于在网络中出现了一个从源点$S$到汇点$T$的流量。

分析一下题目：同一个柱子的小球要求可以与前一个小球形成和为完全平方数的情况，当一个新的小球到来的时候，可以加入其中的一根柱子，当然也可以另外开启一个新的柱子，使用的柱子的总数不得超过$n$。

我们另开一个节点$T^{\prime }$用来表示柱子的上限，连接一条容量为$n$的边$(T^{\prime },T)$。

我们尝试把小球拆成两个点$B$和$B^{\prime }$，并且由$S$向$B$连接一条容量为$1$的边。由$B^{\prime }$向$T$连接一条容量为$1$的边，为什么容量为$1$？这限制了每个球后面都只能紧邻地放一个球。

如果数大的小球与某个数小的小球之间组合满足和为完全平方数(即大球可以放在小球后面)，我们就从连接一条容量为$1$的边$(B_{大球},B_{小球}^{\prime })$。这代表该大球可以放在小球后面不需要开启新的柱子。

每个球都可以连接一条容量为$1$的边$(B,T^{\prime })$。代表该小球独立开启了一个新的柱子。

如下图所示：

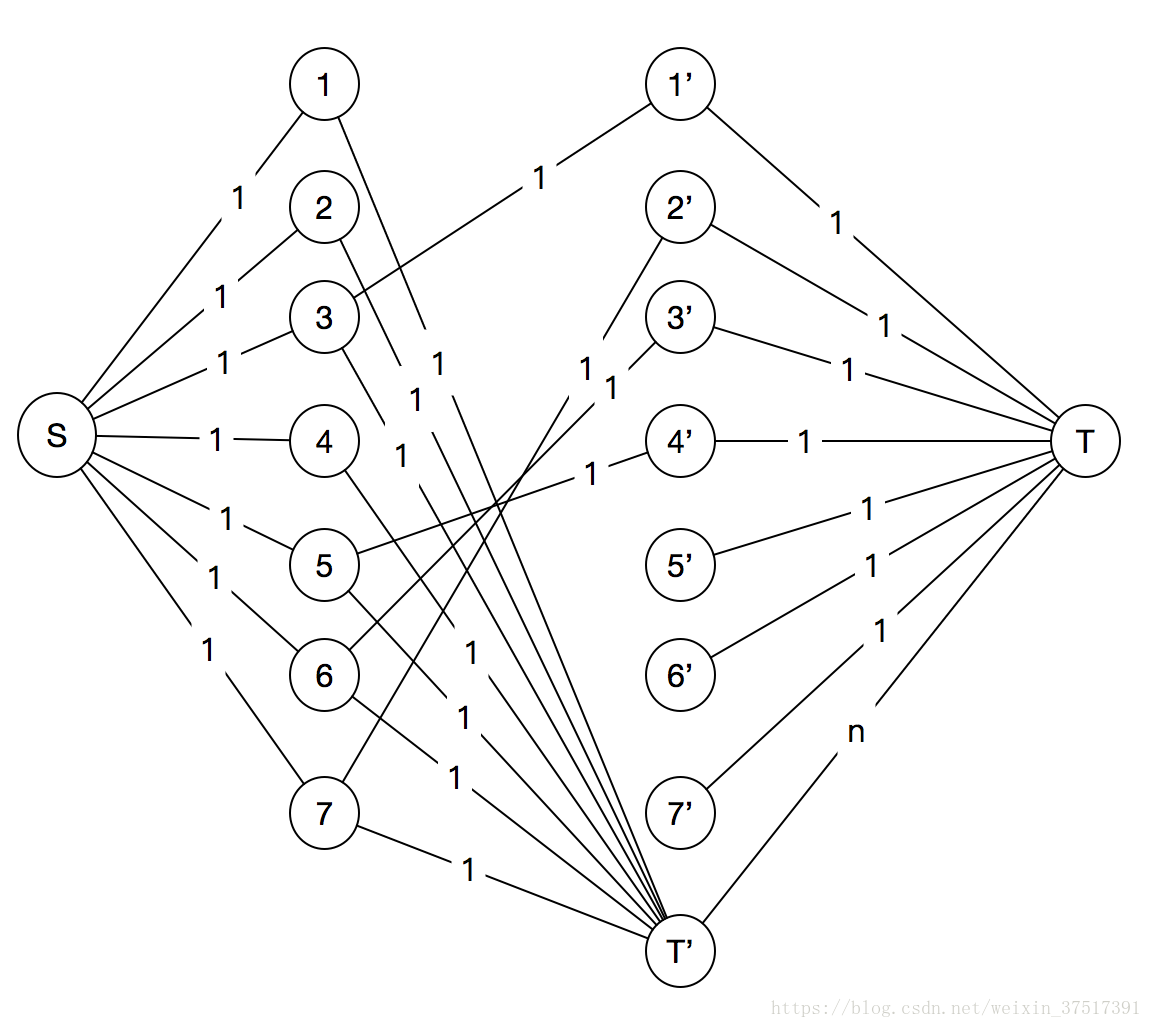
回顾一下这张图：
从$B$流向$T^{\prime }$的流量代表$B$球开启了一个新的柱子，而从$B_{大球}$到$B_{小球}^{\prime }$的流量代表$B_{大球}$放在了$B_{小球}$的后面。

这只是建图模型，我们在解决这道题的时候不能跑一遍网络流完事，而是需要使用迭代加深搜索的思想，增量式建图，每次加入一个球，然后在残余网络中跑最大流，判断能否跑满，如果跑不满，那么答案就是上次跑满时候的结果。

最后，这道题要求输出方案，我们只需要在残余网络里面遍历去边的容量，然后就可以得到方案了，这里不必细说，看我的代码就可以了。

参考代码 见附录

放置、匹配的问题，都可以往网络流方面思考。

---

P2764 最小路径覆盖

什么是最小路径覆盖？

最小路径覆盖分为两种

• 最小不相交路径覆盖
• 最小可相交路径覆盖

最小不相交路径覆盖的做法

构造一个新图，将一个点$B$拆成$B_1$和$B_2$两个点，在原图中如果有边$(A,B)$那么在新图中连接边$(A_1,B_2)$。
然后形成了一张二分图，结论就是最小不相交路径覆盖=原图节点数-二分图的最大匹配。

如何理解这个过程呢？

一开始每个点都是一条路径。
在二分图中，每形成一个匹配，就相当于一条路径将匹配两边的点给合并了，也就是合并了两个路径，这样一直匹配下去，路径数就在不断的减少，所以最终形成的就是最小路径覆盖，最后的路径数就是一开始原图的节点数-匹配数。

最小可相交路径覆盖的做法

这个问题与本题没有关系，只是扩展，可以暂时跳过。
解这个小问的方法是把这个问题化归到最小不相交路径覆盖上去。

可相交也就是说如果两点可达，那么不管这两点中间有多少节点，我都可以去经过。

先跑出可达矩阵，用Floyd算法，算出两两点之间的可达性。
然后如果两两可达，则建边。建成新图以后，就变成了最小不相交路径覆盖问题了。

理解

但是如果两个点a和b是连通的，只不过中间需要经过其它的点，那么可以在这两个点之间加边，那么a就可以直达b，不必经过中点的，那么就转化成了最小不相交路径覆盖。

这道题同样需要输出方案，在残余网络中遍历边处理就可以了。

参考代码 见附录

---

P2763 试题库问题

我觉得这是一个非常典型的二分图问题。

$k$种类型是二分图左侧的$k$个点。

$n$个试题是二分图右侧的$n$个点。

如果某试题属于某种类型，就在试题和类型之间连接一条边，容量为$1$。

要求选出$num$个$t$类型的题目，那么就在源点$S$和$t$类型点之间加入一条容量为$num$的边。

而每道题目只能使用一次，因此在题目$p$和汇点$T$之间连接一条容量为$1$的边。

然后跑一遍最大流就可以得到答案了。

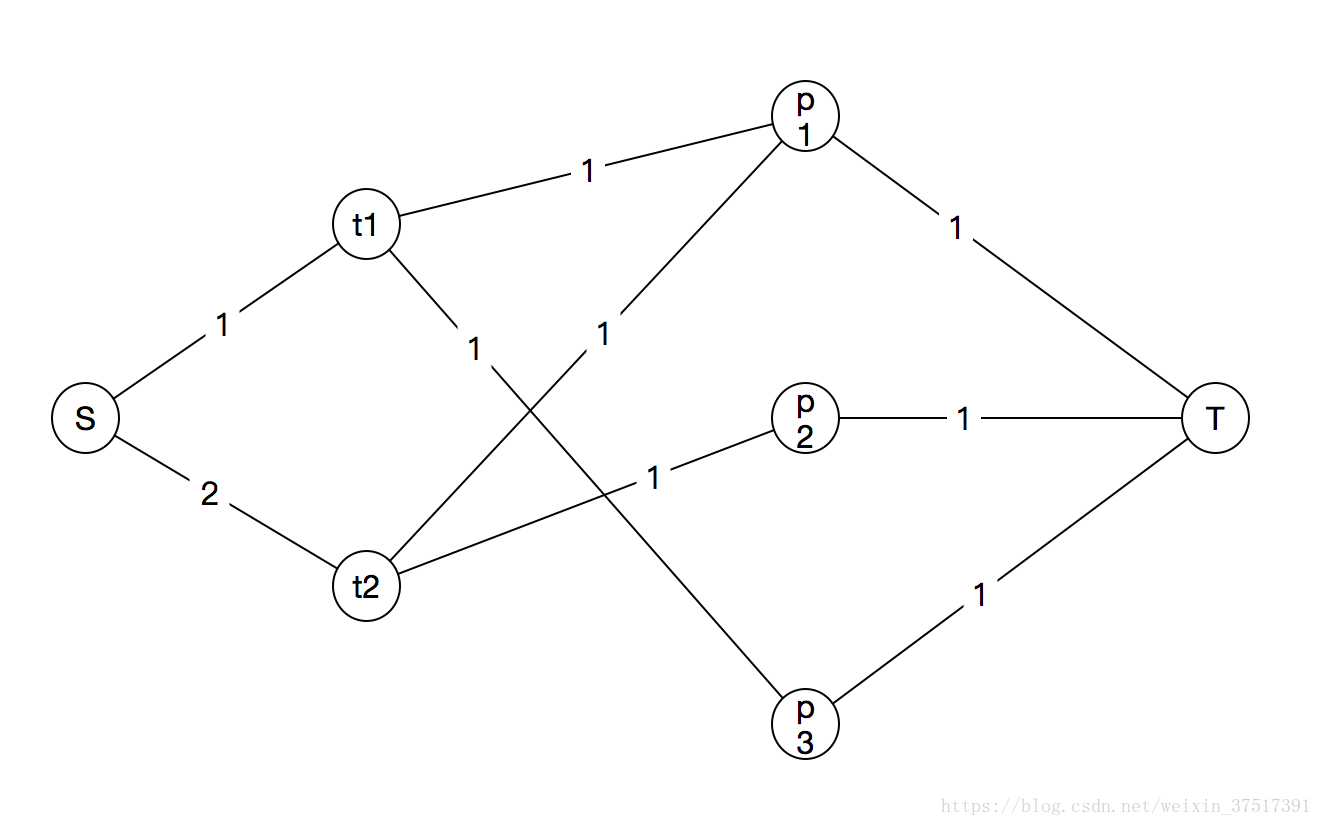
参考代码见附录

---

P2766 最长不下降子序列问题

这类问题属于动态规划方程已知，对解方案计数的问题。
还有的是要求最短路的数量的问题，我之前有在我的博客里写过，感兴趣的各位可以找找看。

第一问

要求求出最长不下降子序列长度，这个使用动态规划很容易解决，但是我们必须要在这一步中处理出以$a[i]$元素为结尾的最长非降子序列的长度数组$f[i]$。

第二问

要求在所有的点都不能重复使用的时候，能找到多少个最长非减子序列。

在网络流处理问题的模型中，如果一个点不能重复利用，那么我们可以将这个点$P$拆成两个点$P_s$和$P_t$，并由$P_s$向$P_t$连接一条容量为$1$的边。所有流入这个点的边都与$P_s$相连，所有流出这个点的边都与$P_t$相连。

在这个题中，我们从f[i]f[i]