前言
不断更新中…
专题的(下)篇将介绍网络流的一些奇奇怪怪的应用和费用流有关的一些套路。
本专题暂时包含三道题:
洛谷P1251 餐巾计划问题: 费用流的基本应用
Trade Gym - 100212I: 使用网络流对图论中的边进行调整
codeforces 818G - Four Melodies: 费用流压缩建图
洛谷P1251餐巾计划问题
题意
题解
这道题我们把选取一张餐巾纸当作是一个单位的流量,那么显然来源部不同的餐巾纸,他们的费用是不相同的,这就引出了费用流(最小费用最大流)的模型。
每一天可以在早上接受 r[i] r [ i ] 数量的餐巾纸,同时也可以将 r[i] r [ i ] 数量的餐巾纸送去清洗,所以我们需要将每一天拆成两个点,分别表示需要餐巾纸的点和送走餐巾纸的点。
需要餐巾纸的点与汇点
T
T
连边,容量为,费用为
0
0
。还要和源点连边,容量为
r[i]
r
[
i
]
,费用为
p
p
,这代表购买新的餐巾纸的方式。
送走餐巾纸的点需要和两个点进行连边:
- 送去慢洗,则需要和天以后的需求点连边,容量为
inf
i
n
f
,费用为慢洗一条的费用。
- 送去快洗,则需要和 m m 天以后的需求点连边,容量为,费用为快洗一条的费用。
注意,由于一条餐巾纸洗完了可以存放任意时间,所以我们需要在相邻需求点之间连立一条费用为 0 0 ,容量为的边,代表的含义就是餐巾纸在存放。
如图所示:
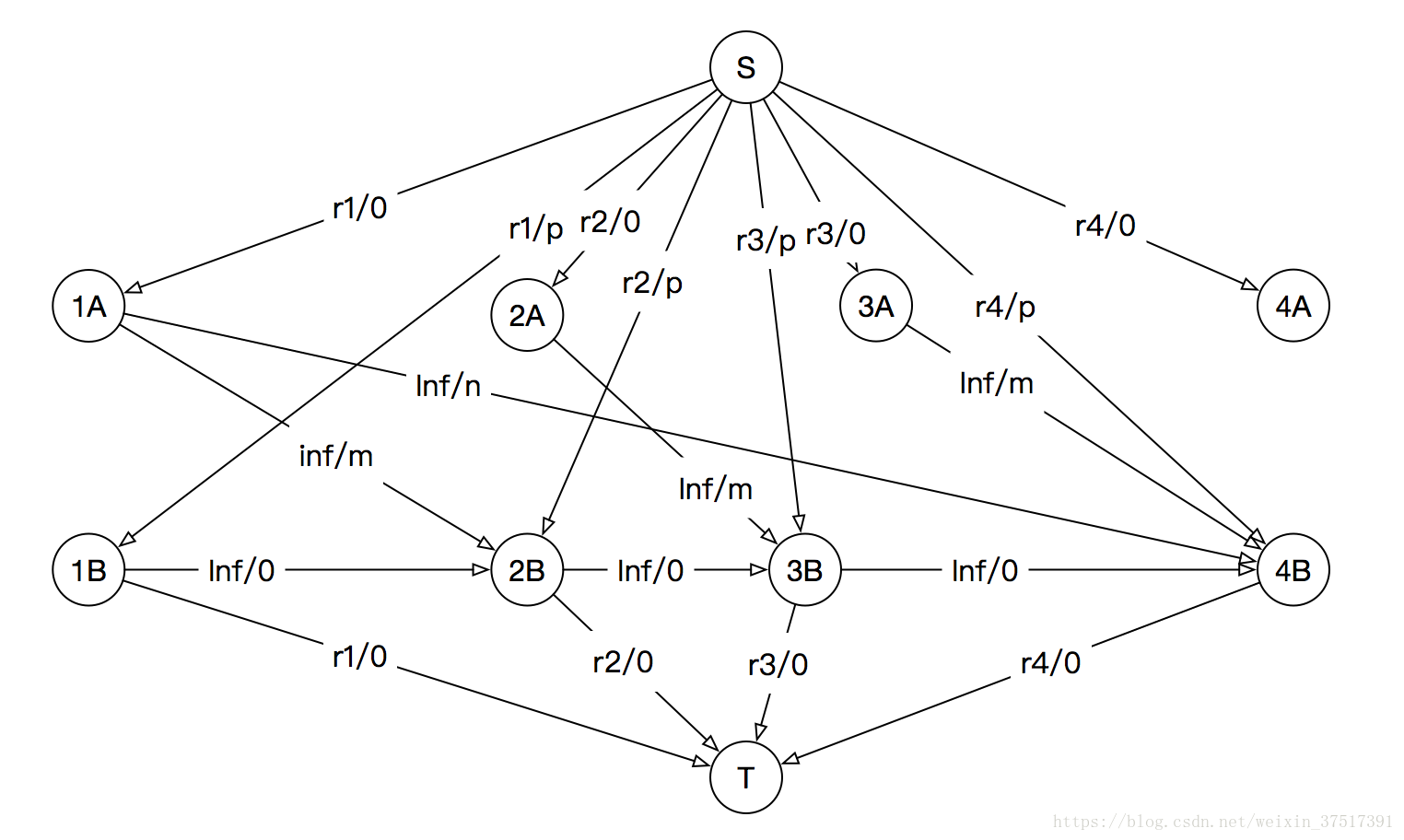
优化:由于 B B 累点之间有边相连,表示餐巾纸可以存放到下一天,那么,我们可以把的边省略掉,只保留 S−>1B S − > 1 B 这条边,表示所有新购买的餐巾纸都在第一天买好,然后存放到需要的那一天再使用。
优化图如下:
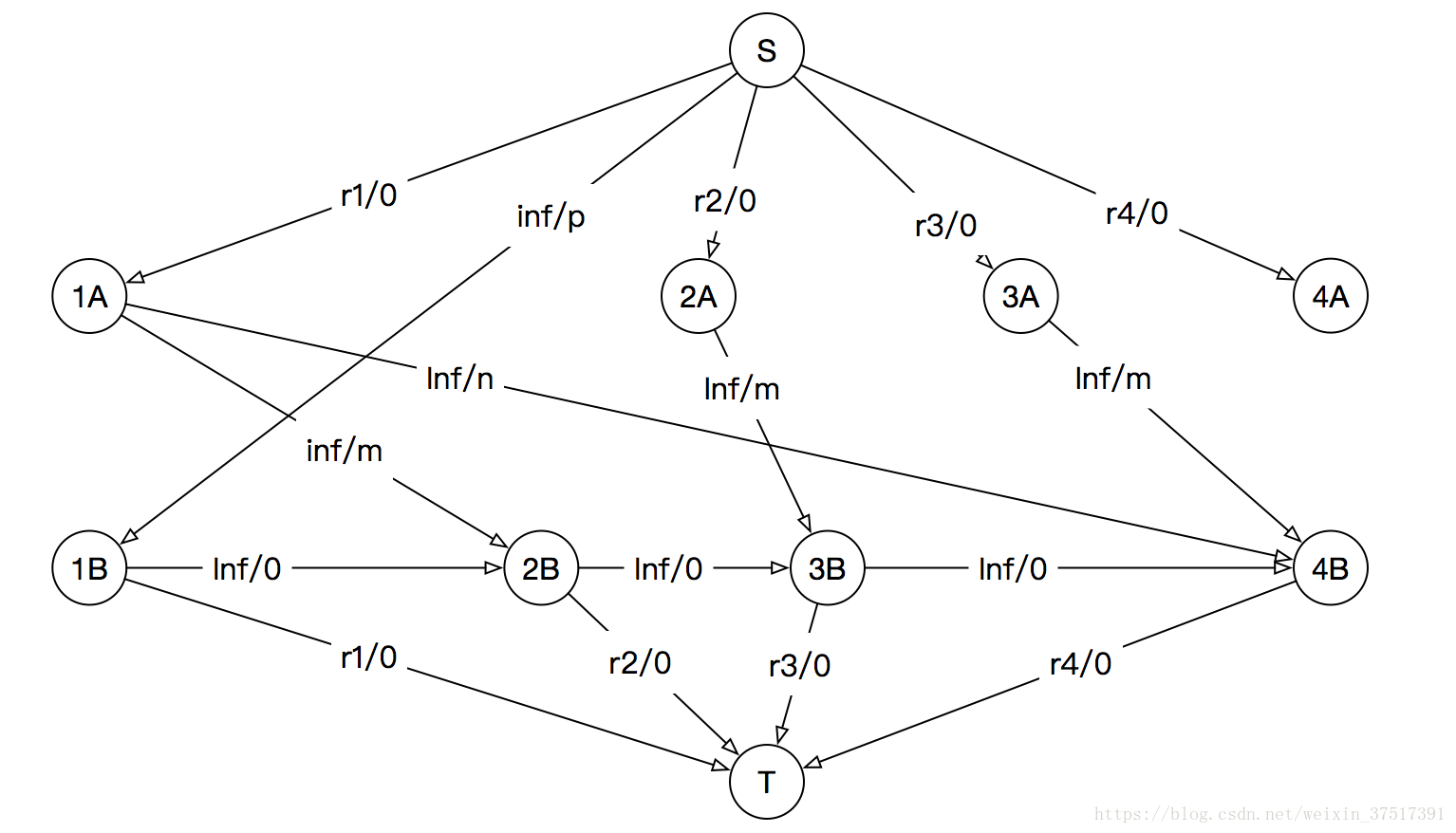
这样建图完成以后,跑一个最小费用最大流就可以了。
注意:请检查你的板子速度是否可行,我的板子速度就太慢了,zkw费用流模板了解一下。参考代码 略
Trade Gym - 100212I
题意
给出A、B两个点集,A、B之间有边相连,而A和B的内部均无边相连。
题目要求求出最多删除A、B之间的多少边,才能使得A中点的度数至少都为2,B中点的度数也至少都为2。题解
先求出每个点的度数,从每个点v出发,最多能删除 deg[v]−2 d e g [ v ] − 2 条边(注意这里是理想情况下,不一定能删除这么多)。
那么我们就可以建立一个超级源点 S S 和超级汇点,从 S S 往点集连边,边的容量为 deg[v]−2 d e g [ v ] − 2 ,从 B B 点集往点连边,边的容量为 deg[u]−2 d e g [ u ] − 2
A A 和之间的边流量全为 1 1 。
从点流到 T T 的每一个为的流量,都相当于在原图里面删除了这条边。
跑一边最大流,就可以得到最多能删除多少边了。在残余网络中做一些小操作就可以把剩余的边输出出来。
网络图如下:
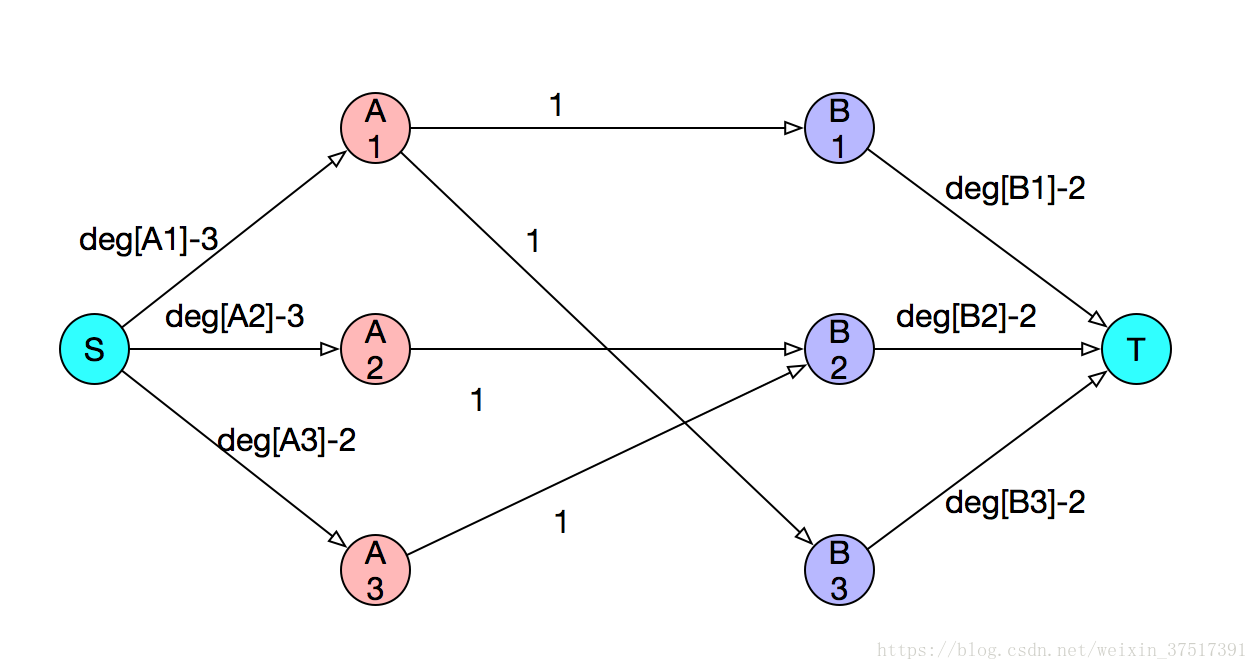
总结
网络流可以用于对图论中的边进行调整,当图论中的一条边存在流量流过的时候,代表该边被“调整”了,调整可以具有很多含义,比如本题中的“删除”也算“调整”。
参考代码 略
Four Melodies
题意
给出 n n 个数,输出选四个不相交的melody的所有情况中,4个melody长度总和的最大值。
要形成Melody,要求相邻的数字要么相差,要么相差 7 7 的倍数。
题解
一种很直观的建图方法就是把每个数字拆成2个点和 out o u t ,然后源点也拆成2个点 s s 和,并把 s′ s ′ 作为费用流的源点。
从 s′−>s s ′ − > s 建立一条容量为 4 4 费用为的边。然后从 s s 点向每个建立一条容量为 1 1 ,费用为的边。
再从 in i n 向 out o u t 建立一条容量为 1 1 ,费用为的边。从 out o u t 向汇点 t t 建立一条容量为,费用为 0 0 的边。
然后对于任意两个如果 i i 到符合相邻的 2 2 个条件,那么就从i的点向j的 in i n 点连接一条容量为 1 1 费用为的边,表示他们可以串起来。
这样的话,建图的复杂度为 O(n2) O ( n 2 ) ,边的个数也为 O(n2) O ( n 2 ) ,复杂度太高了,因此需要压缩建图。
奇技淫巧:当你找不到任何优化的点的时候,可以考虑搞一个出错率极小的做法,有一个想法就是每个点仅向后面50个点连边。
怎么压缩建图呢?
把每个点都扩充成3个点 in,mid,out i n , m i d , o u t ,其中 in i n 往 mid m i d 连边容量为 1 1 ,费用为, mid m i d 往 out o u t 连边,容量为 1 1 ,费用为。
从 in i n 往 out o u t 连边容量为 inf i n f ,费用为 0 0 ,表示途径这个点。
关键的一步来了:
从i这个点往后找第一个使得的点 j j ,从向 j.in j . i n 连接一条容量为 1 1 ,费用为的边。
从 i i 这个点往后找第一个使得的点 j j ,从向 j.in j . i n 连接一条容量为 1 1 ,费用为的边。
从i这个点往后找第一个使得 (val[i]−val[j])%7==0 ( v a l [ i ] − v a l [ j ] ) % 7 == 0 的点 j j ,从向 j.in j . i n 连接一条容量为 1 1 ,费用为的边。
这样的话,图就算压缩完成了(不需要两两比较建图)。
图举例:
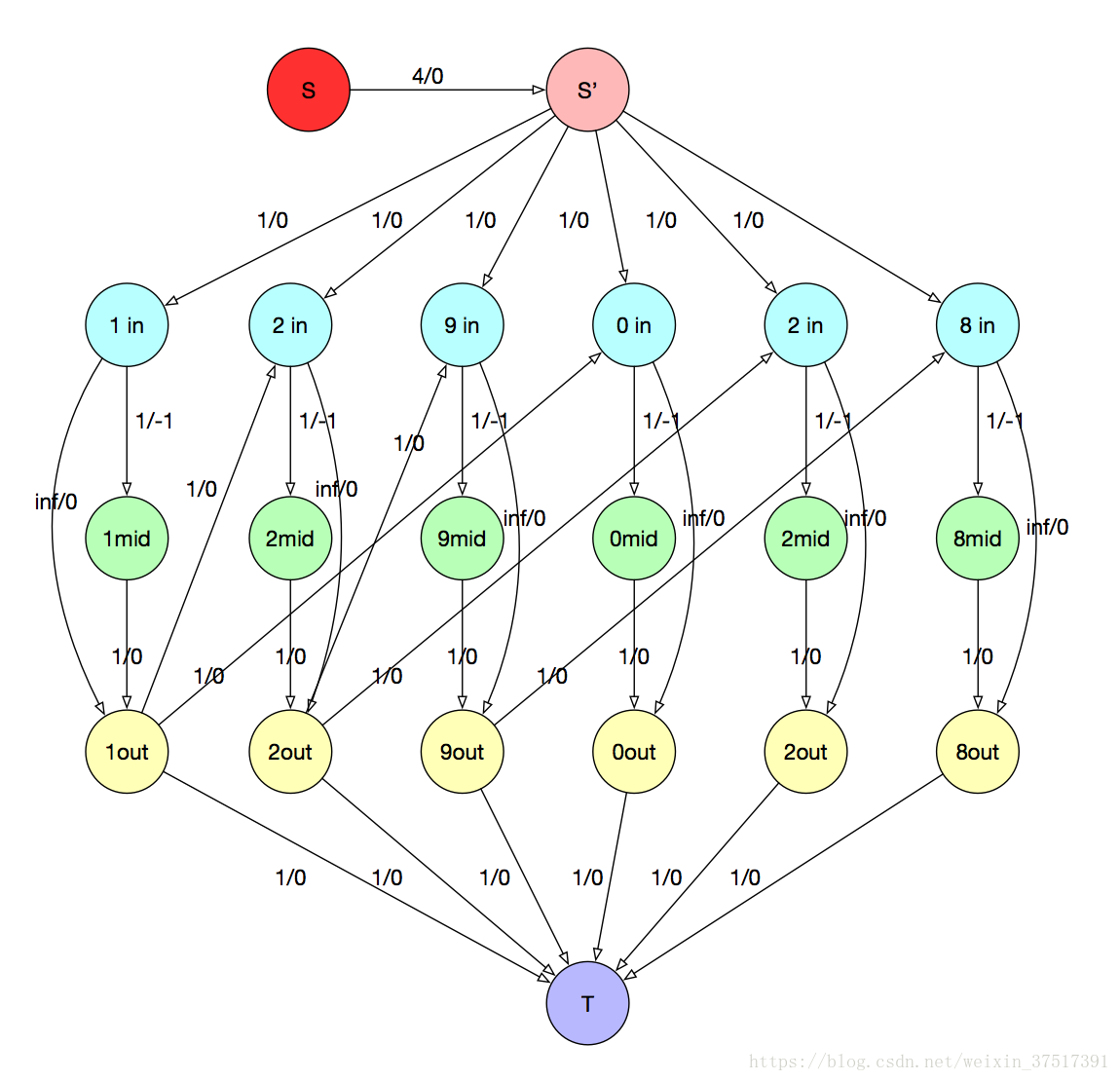

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








