均匀分布的概率密度函数_理解概率密度函数

原创声明：本文为 SIGAI 原创文章，仅供个人学习使用，未经允许，不能用于商业目的。

其它机器学习、深度学习算法的全面系统讲解可以阅读《机器学习-原理、算法与应用》，清华大学出版社，雷明著，由SIGAI公众号作者倾力打造。

• 书的购买链接
• 书的勘误，优化，源代码资源

概率密度函数是概率论中的核心概念之一，用于描述连续型随机变量所服从的概率分布。在机器学习中，我们经常对样本向量x的概率分布进行建模，往往是连续型随机变量。很多同学对于概率论中学习的这一抽象概念是模糊的。在今天的文章中，SIGAI将直观的解释概率密度函数的概念，帮你更深刻的理解它。

从随机事件说起

回忆我们在学习概率论时的经历，随机事件是第一个核心的概念，它定义为可能发生也可能不发生的事件，因此是否发生具有随机性。例如，抛一枚硬币，可能正面朝上，也可能反面朝上，正面朝上或者反面朝上都是随机事件。掷骰子，1到6这6种点数都可能朝上，每种点数朝上，都是随机事件。

与每个随机事件a关联的有一个概率值，它表示该事件发生的可能性：p(a)这个概率值必须在0到1之间，22即满足下面的不等式约束：

0<= p(a)<=1

另外，对于一次实验中所有可能出现的结果，即所有可能的随机事件，它们的概率之和必须为1：

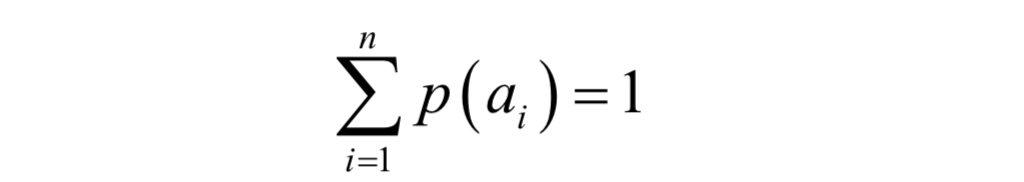
这些随机事件不会同时发生，但必须有一件会发生。例如，对于抛硬币，不是正面朝上就是反面朝上，不会出现其他情况（这里假设硬币抛出去后不会立着），因此有：

p(正面朝上)+p(反面朝上)=1

很多时候，我们假设这些基本的随机事件发生的概率都是相等的，因此，如果有n个基本的随机事件，要使得它们发生的概率之和为1，则它们各自发生的概率都为：