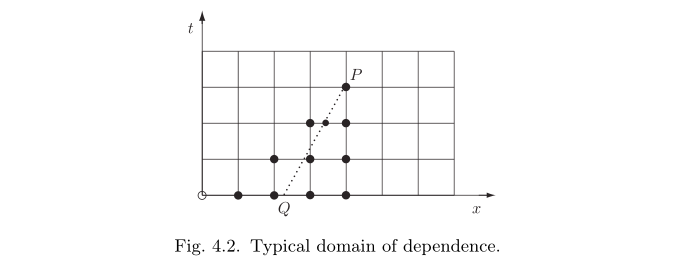
从今天开始进入双曲型方程的差分方法构造. 主要介绍几个常见的常系数对流方程的构造方法以及CFL方法。下一次我们来复习常系数对流方程差分格式的其他研究手段。
与抛物型方程相比, 双曲线方程缺乏耗散机制, 相应数值困难更为突出.
参考书:
(1) J.W. Thomas - Numerical Partial Differential Equations_ Finite Difference Methods (1995, Springer)
(2) 张强《偏微分方程的有限差分方法》科学出版社,2019年1月版。
(3) K. W. Morton, D. F. Mayers - Numerical solution of partial differential equations (2005, Cambridge University Press)
今天内容:
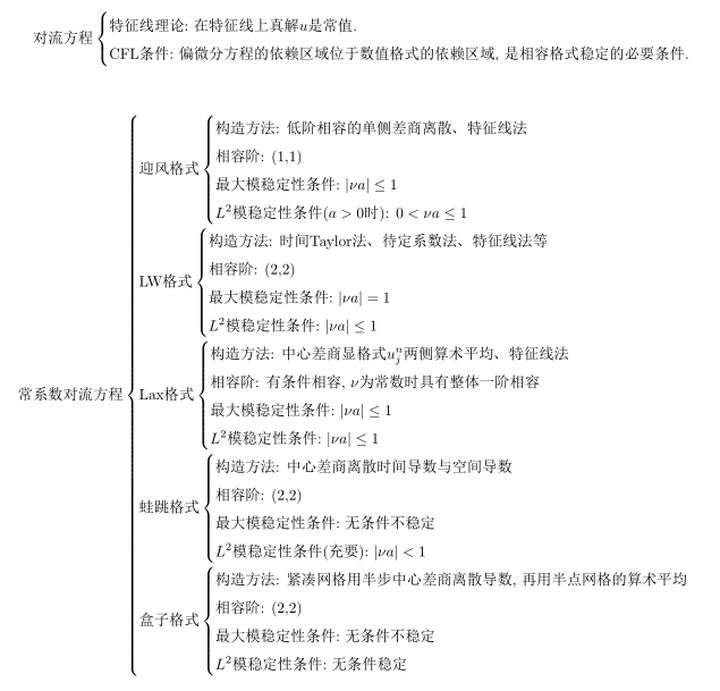
1 对流方程的特征线
考虑最简单的对流方程
的纯初值问题或周期边值问题, 初值为
特征线就是下面ODE的所有解:
在每条特征线上, 解
利用初值, 可以选择一系列合适的点
如果
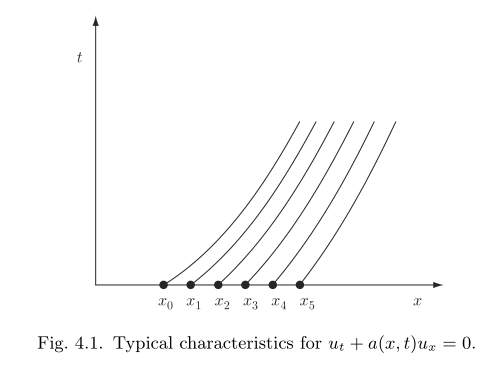
当
特征线为一束平行直线
对于非线性问题, 如果
但是此时特征线可能会相交.
2 基本格式、CFL条件
设








 本文深入探讨了常系数对流方程的差分方法,包括中心差商显格式、迎风格式、Lax-Wendroff格式,并详细阐述了CFL条件及其在各种格式中的应用。同时,介绍了Lax-Friedrichs、蛙跳和盒子格式,分析了它们的稳定性和阶数。
本文深入探讨了常系数对流方程的差分方法,包括中心差商显格式、迎风格式、Lax-Wendroff格式,并详细阐述了CFL条件及其在各种格式中的应用。同时,介绍了Lax-Friedrichs、蛙跳和盒子格式,分析了它们的稳定性和阶数。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 15
15

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








