各层作用_楼面阻尼器作用下高层钢框架结构抗震控制研究

随着高层建筑的发展，人们对于结构振动控制的要求也越来越高。传统设计方法仅仅通过增加结构的刚度、阻尼以及改变结构的质量分布来提升结构的性能，以抵抗强风和强震对于结构的影响^[1]。而振动控制是通过由结构-抗风抗震控制系统主动控制结构的动力反应^[2]。为了更好地实现结构振动控制系统在实际工程中的使用，SADEK等^[3]提出了一种以结构-调谐质量阻尼器(tuned mass damper，TMD)系统前二阶模态的阻尼比相等且最大为目标并适用于有阻尼结构的最优参数公式，实现对阻尼器参数的优化。秦丽等^[4]自编计算程序，对比分析了四种TMD参数的优化准则，对这四种方法确定的参数在地震动作用下的控制效果进行了分析比较。徐怀兵等^[5]、欧进萍等^[6]研究了TMD结构振动控制的理论、参数与试验的设计方法，对设置了TMD的结构进行振动控制分析，并提出多TMD作用下振动控制的优化方法。

虽然国内外学者都对结构耗能减震控制进行了研究，但各国对此类问题都没有充分的设计依据和统一标准，对耗能减震阻尼器的最优化设计研究力度不够，特别是对耗能减震阻尼器的布置优化和参数优化的研究相对缺乏。随着调频质量阻尼器在高层建筑结构中的运用越来越普遍，研究其对结构振动的控制具有较为重要的意义。

01

工程实例

1.1 工程背景

该工程为新建的湖南广播电视台节目生产基地演播厅F及漂浮办公室，建筑高度为50.11m，由演播厅、支撑筒、漂浮办公室三部分组成，如图1所示。1~6层为演播厅F，是普通钢框架结构；8~9层的漂浮办公室为钢框架结构，由钢梁、钢柱以及斜支撑组成，支承在两排总共10个支撑筒结构上，最大跨度为33.6m，最大悬挑达12m。结构抗震设防烈度为7度，由于其特殊的结构形式，受到风荷载和地震作用时，极易产生振动。因此，在漂浮办公室楼面上设置TMD对结构的振动进行控制，以提高结构的舒适度和安全性。

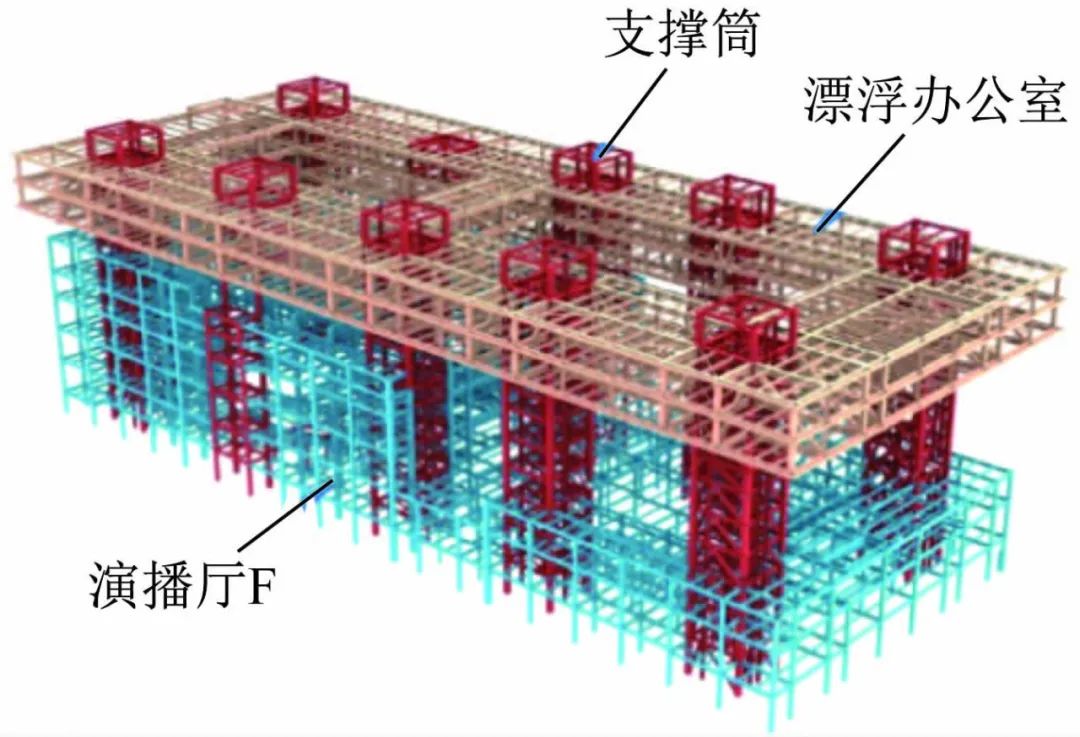
图1 项目结构组成

Fig.1 Project structure composition

1.2 有限元模型的建立

运用SAP2000建立布置了楼面阻尼器的结构空间三维有限元模型，梁柱利用框架单元模拟，楼板采用壳单元模拟。该工程调频质量阻尼器由质量系统、弹簧系统和阻尼系统组成，3个组成系统分别采用点质量、Linear单元和Damper单元来模拟^[7]。阻尼器通过槽钢与主体结构的框架钢梁相连，如图2所示。为比较阻尼器不同布置方式对其振动控制效果的影响，本文预设了三种阻尼器布置方案，如图3所示。

方案1：在漂浮办公室8层和9层两端内侧设置4个楼面阻尼器；

方案2：在每个支撑筒的顶端设置2个阻尼器；

方案3：在漂浮办公室8层和9层两端外侧设置4个楼面阻尼器。

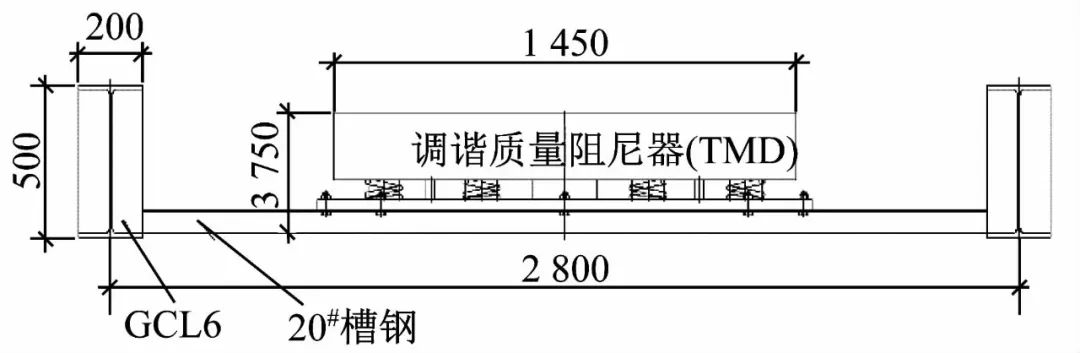
图2 TMD与主体结构连接(单位：mm)

Fig.2 Connection between TMD and main structure(Unit：mm)

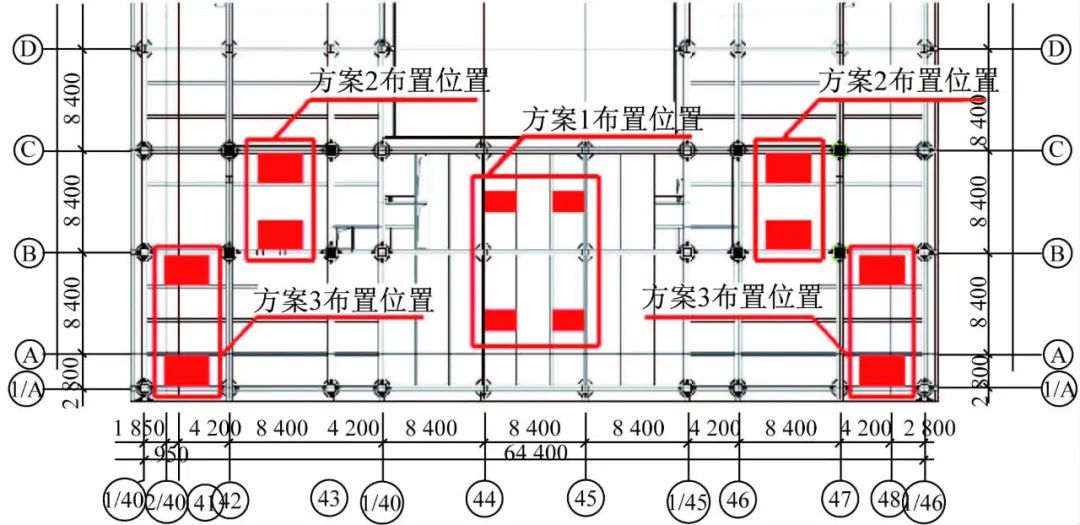
图3 TMD布置方案

Fig.3 Scheme of TMD layout

三种方案阻尼器的布置位置不同，但阻尼器总个数相同，都为16个，且每个阻尼器各项参数也相同，排除其他因素对结构振动控制效果的影响。由于篇幅有限，本文主要研究阻尼器的布置位置对楼面振动控制的效果。

1.3 阻尼器设计及模态分析

为最优化阻尼器的各项参数达到其最佳控制效果，本文引用文献[3]公式对阻尼器各项参数进行优化。TMD的频率比和阻尼比可分别由式(1)、式(2)计算：

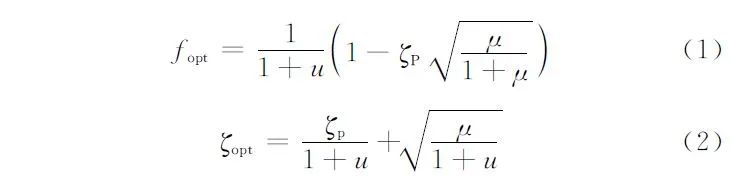
该工程为纯钢框架结构，结构阻尼比取0.02，TMD的质量比取0.01，通过模态分析得到结构第1阶自振频率为1.695Hz。采用上述公式和参数优化后的TMD参数如表1所示。

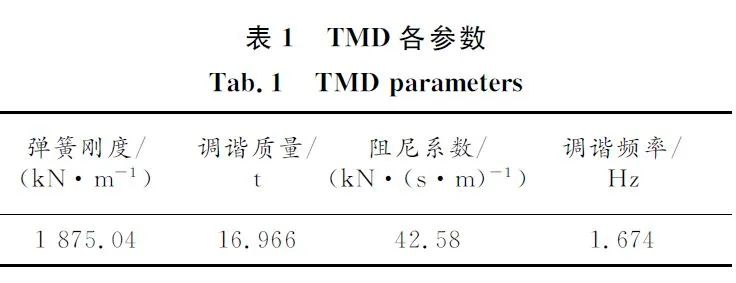
将参数优化后的阻尼器施加于结构，利用SAP2000对施加阻尼器和未施加阻尼器结构进行模态分析得到结构前五阶自振周期，如表2所示。

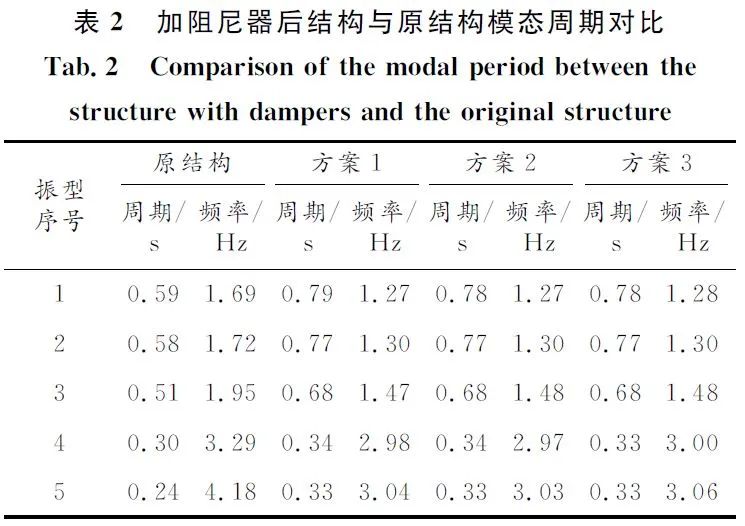
可以看出，布置阻尼器后结构的一阶周期较原结构延长率都为34%，周期有明显的增加。结构自振周期的延长，可有效避免共振现象的发生，使结构远离场地土的卓越周期^[8]，减小地震对结构的破坏。由于结构的自振周期与结构的质量及刚度有关，本结构三种方案的阻尼器各参数相同，结构的总质量和刚度基本一致，因此三种方案作用下结构的周期变化不大。

02

地震动力特性分析

2.1 地震波的选取

该工程位于湖南省长沙市，为二类地区，根据《建筑抗震设计规范》(GB 50011—2010)^[9](简称《抗规》)要求，采用时程分析法时，实际强震记录数量不可以小于总数的2/3，为满足上述要求，本文选取3条波：El Centro波、唐山波与人工波4。本文时程分析所使用的罕遇地震加速时程最大值为220cm·s^-2，通过系数将3条波的加速度峰值都调整为220cm·s^-2，如表3所示。

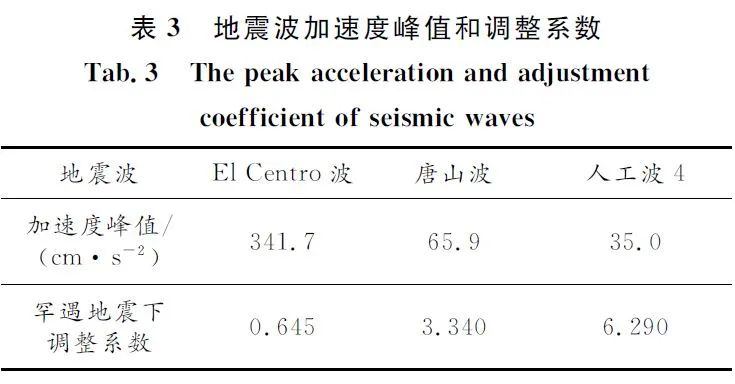
根据结构布置，可知本结构y向刚度远远大于x向刚度，故x向受地震激励时振动响应会更加剧烈。本文仅研究结构受x向地震作用下的动力响应。

2.2 层间剪力分析

结构受水平地震荷载作用时，层间剪力的大小直接影响结构的破坏形态，因此层间剪力是度量结构抗震性能的重要指标^[10]。对安装了楼面TMD的结构，可以直接用层间剪力的大小衡量阻尼器的抗震效果。通过时程分析，提取不同地震波作用下各方案结构的层间剪力最大值，绘制各结构的层间最大剪力变化曲线如图4所示。

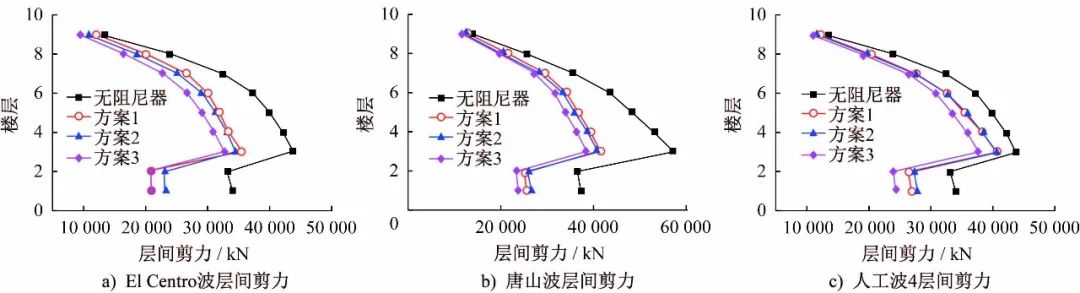
图4 四种方案结构地震波下各层最大层间剪力

Fig.4 Maximum inter-story shear of four schemes  under seismic waves

可以看出，与原结构相比，受楼面TMD控制下的结构各层层间剪力最大值都有了较大幅度的减小。从分析数据可知，水平地震荷载作用下，原结构3层处层间剪力为结构最大层间剪力，其值为56,993kN，方案3楼面TMD控制下的结构3层处层间剪力为38,384kN，最大层间剪力减小了近33%，阻尼器对结构层间剪力的控制效果较好。对比分析各方案在3条波作用下底层层间剪力，结果表明方案3对底层层间剪力的减小量分别达到37.0%、36.2%、28.4%，为最佳层间剪力控制方案。

2.3 顶层加速度分析

顶层加速度值和位移值直接反映了结构受地震作用时的振动程度，是衡量楼面TMD抗震效果的重要参数。统计有限元分析结果，将楼面TMD对结构顶层加速度和位移减小率统计列于表4~6。结果表明，在罕遇地震作用下，楼面TMD对结构顶层加速度的最大减小率为56.1%，对结构顶层位移的最大减小率为38.1%，阻尼器减振效果较好，且方案3为最佳控制方案。

表4 El Centro波作用下TMD对结构振动的减小率

Tab.4 Reduction rate of TMD for structural vibration under EI Centro wave  % 

表5 唐山波作用下TMD对结构振动的减小率

Tab.5 Reduction rate of TMD for structural vibration under Tangshan wave  %

表6 人工波4作用下TMD对结构振动的减小率

Tab.6 Reduction rate of TMD for structural vibration under artificial wave 4  %

2.4 层位移分析

层位移的大小直观地反映了结构变形的幅度，是判别结构在地震作用下动力响应的重要指标。通过时程分析，得到三种方案下结构各层的最大层位移值，如图5所示。

可以看出，随着楼层的增加，结构的层位移也越大，而楼面TMD对结构层间位移的减小率随结构楼层的增加而增加，三种阻尼器布置方案对结构顶层的位移控制率均为30%左右。对位移的有效控制使结构更趋向于整体平动，有效地减小了在地震作用下楼层之间位移产生的内应力。对比三种方案，方案3对结构层间位移的控制效果最好，因此为最佳振动控制方案。

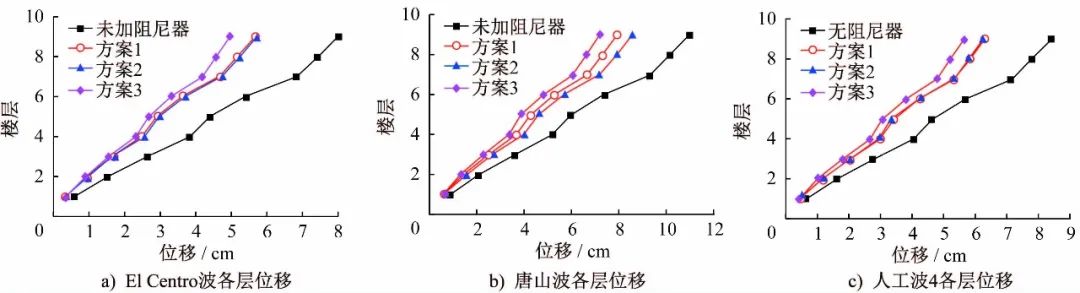
图5 四种方案结构地震波下各层最大层位移

Fig.5 Maximum story displacement of four schemes under seismic waves

2.5 质量比对TMD振动控制效果影响分析

层间位移角是结构使用功能的重要指标^[11]，可以有效地反映结构的变形程度。在方案3的基础上，预设五种不同质量比的TMD布置在楼面结构，质量比分别为0.5%、1%、1.5%、2%、2.5%。通过有限元分析，得到结构在不同地震波作用下各层的层间位移角，如图6所示。

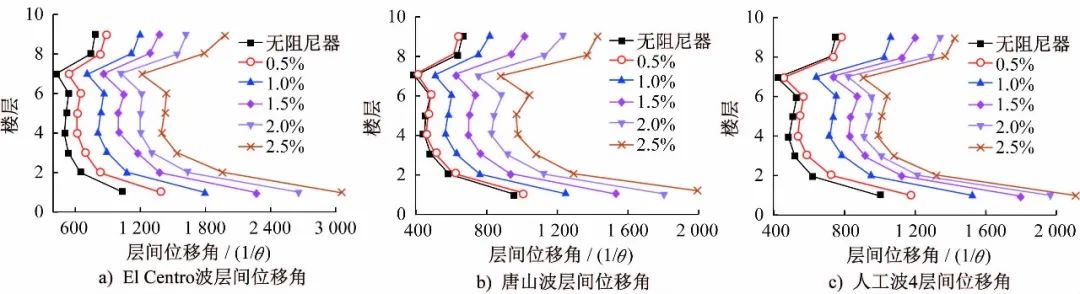
图6 不同质量比TMD作用下结构各层层间位移角对比

Fig.6 Comparison of inter-story drift of structures under TMD with different mass ratio

可以看出，当质量比为0.5%时，楼面TMD对结构的振动控制效果较差，甚至不起作用。而1%及以上质量比的TMD阻尼器可以有效地控制结构的层间位移角，使结构地震作用下的变形更加平稳，有效减小了结构在地震作用下的应力集中。随着质量比的增加，楼面TMD对振动的控制效果也逐渐提高，使结构层间位移角小于《抗规》要求的抗震性能指标。

03

结  论

本文通过时程分析验证了楼面TMD对高层钢框架结构振动控制的有效性，可以得出以下主要结论：

(1)在质量比为1%的楼面阻尼器作用下，结构周期增加34%，有效避免了共振现象的发生，可减轻地震灾害。同时随着楼层的增加，楼面TMD对结构的控制效果会越好，使结构变形更趋向于平动，结构的振动得到有效控制。

(2)阻尼器系统布置在楼面外侧效果较好，结构顶层最大加速度减小率约为50%，最大位移减小率约为20%，层间最大剪力减小率约为37%。

(3)TMD的质量比过小会影响其控制效果，当质量比不大于2.5%时，随着质量比的增加，TMD对于结构振动控制效果会越佳。

综上所述，类似本文工程顶部——带有大悬挑的高层钢框架结构，可将楼面阻尼器布置在结构的靠外侧，同时适当增加楼面阻尼器的质量比以达到最佳的振动控制效果。

参考文献

[1]周福霖.工程结构减震控制[M].北京:地震出版社,1997.ZHOU Fulin.Seismic control of engineering structures [M].Beijing:Seismological Press,1997.(in Chinese)

[2]李宏男,孙丽.结构在多维地震动作用下抗震计算组合方法[J].大连理工大学学报,2003,43(3):338-343.LI Hongnan,SUN Li.Modal combination method for earthquake-resistant design of structures to multiple seismic excitations[J].Journal of Dalian University of Technology,2003,43(3):338-343.(in Chinese)

[3]SADEK F,MOHRAZ B,TAYLOR A W,et al.A method of estimating the parameters of tuned mass dampers for seismic applications[J].Earthquake Engineering Structural Dynamics,1997,26(6):617-635.DOI:10.1002/(SICI)1096-9845(199706)26∶6<617∶∶AID-EQE664>3.0.CO.

[4]秦丽,闫维明,呼学军,等.河南艺术中心标志塔TMD地震控制[J].北京工业大学学报,2009,35(6):761-768.QIN Li,YAN Weiming,HU Xuejun,et al.Study on seismic control effectiveness of TMD system of symbolic tower of Henan Art Center [J].Journal of Beijing University of Technology,2009,35(6):761-768.(in Chinese)

[5]徐怀兵,欧进萍.设置混合调谐质量阻尼器的高层建筑风振控制实用设计方法[J].建筑结构学报,2017,38(6):144-154.DOI:10.14006/j.jzjgxb.2017.06.016.XU Huaibin,OU Jinping.Design method for wind-induced vibration control of high-rise buildings with hybrid tuned mass damper [J].Journal of Building Structures,2017,38(6):144-154.DOI:10.14006/j.jzjgxb.2017.06.016.(in Chinese)

[6]欧进萍,王永富.设置TMD、TLD控制系统的高层建筑风振分析与设计方法[J].地震工程与工程振动,1994,14(2):61-75.DOI:10.13197/j.eeev.1994.02.005.OU Jinping,WANG Yongfu.Wind induced vibration analyses and design methods of tall buildings with tuned mass dampers or tuned liquid dampers[J].Earthquake Engineering and Engineering Vibration,1994,14(2):61-75.DOI:10.13197/j.eeev.1994.02.005.(in Chinese)

[7]北京金土木软件技术有限公司,中国建筑标准设计研究院.SAP2000 中文版使用指南[M].2 版.北京:人民交通出版社,2012.Beijing Golden Civil Software Technology Co.,Ltd.,China Institute of Building Standard Design & Research Co.,Ltd.SAP2000 Chinese version use guide[M].2nd ed.Beijing:China Communications Press,2012.(in Chinese)

[8]郝冰,张彦,曲淑英,等.场地卓越周期的计算及其工程应用[J].水利与建筑工程学报,2016,14(5):144-150.DOI:10.3969/j.issn.1672-1144.2016.05.028.HAO Bing,ZHANG Yan,QU Shuying,et al.Calculation of site predominant period and its engineering applications[J].Journal of Water Resources and Architectural Engineering,2016,14(5):144-150.DOI:10.3969/j.issn.1672-1144.2016.05.028.(in Chinese)

[9]中华人民共和国住房和城乡建设部.建筑抗震设计规范:GB 50011—2010[S].2016版.北京:中国建筑工业出版社,2016.Ministry of Housing and Urban-Rural Development of the People’s Republic of China.Code for Seismic Design of Buildings:GB 50011—2010 [S].2016 ed.Beijing:China Architecture & Building Press,2016.(in Chinese)

[10]张彬,苏鹏,于冬冬.层间隔震地震响应分析[J] .中国地质灾害与防治学报,2014,25(3):121-126.DOI:10.16031/j.cnki.issn.1003-8035.2014.03.052.ZHANG Bin,SU Peng,YU Dongdong.The earthquake response analysis of layer interval shock[J].The Chinese Journal of Geological Hazard and Control,2014,25(3):121-126.DOI:10.16031/j.cnki.issn.1003-8035.2014.03.052.(in Chinese)

[11]王峰,史庆轩,王朋,等.高层斜交网格筒结构受力层间位移的计算及其应用[J].建筑结构学报,2019,40(8):181-190.DOI:10.14006/j.jzjgxb.2017.0542.WANG Feng,SHI Qingxuan,WANG Peng,et al.Calculation and application of physical story drift in high-rise diagrid tube structure[J].Journal of Building Structures,2019,40(8):181-190.DOI:10.14006/j.jzjgxb.2017.0542.(in Chinese)

免责提示：文章及图片均转自网络，版权归原作者及原出处所有，如有侵权或原版权所有者不同意转载，请及时联系我们，以便立即删除。