常用的收敛级数整理_微积分本质(10)--泰勒级数

❤️总结❤️

泰勒级数是数学中极其强大的数学近似工具，利用泰勒级数可以在某点用多项式来近似函数，使得多项式的表达比函数的形式更加友好。

• 泰勒多项式/级数的思想是将函数在某一点的值，利用函数的高阶导数的信息来近似
• 泰勒多项式中的每一项都有明确的含义，可以通过图像的函数来找到其对应的含义
• 泰勒级数在一定的取值范围内收敛，收敛的这个范围称为“收敛半径”。与此同时，超过这个取值范围函数值不收敛，我们称其为发散。

✿✿ヽ(°▽°)ノ✿正文✿✿ヽ(°▽°)ノ✿

主要包含以下三部分的内容

10.1 利用导数信息来构建多项式函数

10.2用几何的方式来解释泰勒展开式的第二项

10.3能不能将多项式累加到无限多项

接下来就是正文了~~

10.1 利用导数信息来构建多项式函数

我们看一下

是如何近似的？假设我们想用二次函数来表达

,那么如何选择合适的

才能使得多项式函数差不多与

的图像重合。

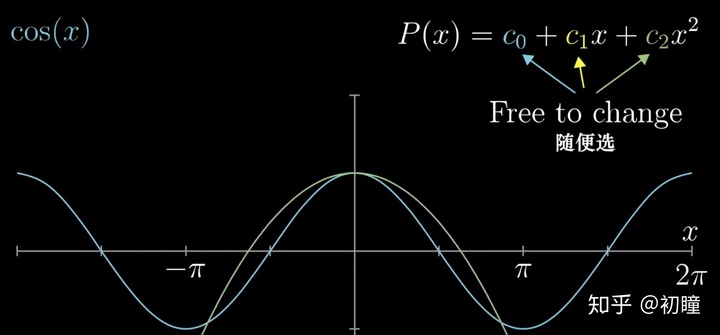
• ①
  处的函数值相等，进而推导出
  
• ②在
  处的
  切线的斜率也能与