马尔科夫链

最新推荐文章于 2025-09-05 14:01:23 发布

转载最新推荐文章于 2025-09-05 14:01:23 发布 · 220 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：https://my.oschina.net/xueyang/blog/387220

文章标签：

#python

2019独角兽企业重金招聘Python工程师标准>>>

马尔科夫链是马尔科夫过程的一个特例，为具备马尔科夫性质与离散时间状态的随机过程。

在马尔科夫链的每一步，系统根据概率分布可以从一个状态到另一个状态，也可以维持当前状态。状态的改变叫做过渡，相应的概率称为过渡概率。随机漫步中移动到每一个点的概率都是相同的，与之前的状态无关。

定义：
- 马尔科夫链是随机变量的一个数列。这些变量的范围，即他们所有可能去治的集合称为状态空间，而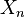得值则是在时间n的状态。用x表示某个状态，则马尔科夫性质可以表示为如下的恒等式。

$P(X_{n+1}=x|X_0, X_1, X_2, \ldots, X_n) = P(X_{n+1}=x|X_n). \,$

性质：
- 可还原性：
  马尔科夫链式有一个条件分布来表示的，称为（一步）转移概率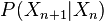， $P(X_{n+1}| X_n)\,$ 。推而广之，二步： $P(X_{n+2}|X_n) = \int P(X_{n+2},X_{n+1}|X_n)\,dX_{n+1} = \int P(X_{n+2}|X_{n+1}) \, P(X_{n+1}|X_n) \, dX_{n+1}$ 三步 $P(X_{n+3}|X_n) = \int P(X_{n+3}|X_{n+2}) \int P(X_{n+2}|X_{n+1}) \, P(X_{n+1}|X_n) \, dX_{n+1} \, dX_{n+2}$
  这些式子可以通过乘以转移概率并求k-1次积分来一般化到任意的将来时间n+k。（换句话说，就是分步累加/积分每一步到下一步的转移概率）。
- 周期性：
  如果状态i每k的整数倍步就会发生一次则称k是i的周期， $k = \gcd\{ n: \Pr(X_n = i \mid X_0 = i) > 0\}$ （值得注意的是，即使该状态周期为k，也有可能不能通过k步到达该状态，比如一个状态可以通过 {6, 8, 10, 12, ...}步到达，虽然周期为2，但是经过2步并不能到达。
  设初始分布为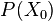，该过程的变化可以用下一个时间步幅表示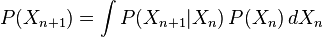： $P(X_{n+1}) = \int P(X_{n+1}|X_n)\,P(X_n)\,dX_n$ ，这时可能存在一个或多个状态分布 $\pi$ 满足 $\pi(X) = \int P(X|Y)\,\pi(Y)\,dY$ ，也就是说存在这样的分布使得其成为平稳分布。当存在至少一个状态经过一个固定的时间段后连续返回，则这个过程被称为是“周期的”。
- 暂返性：（瞎叫的，英文为Transience）: 如果该状态不能返回的概率大于零。
  正式地说，如果存在一个随机变量 T_i 是第一次返回状态i的时间， $T_i = \inf \{ n\ge1: X_n = i \mid X_0 = i\}.$ ， $f_{ii}^{(n)} = \Pr(T_i = n)$ 是n步后第一次返回状态i的概率。如果 $\Pr(T_i < {\infty}) = \sum_{n=1}^{\infty} f_{ii}^{(n)} < 1.$ ，那么状态i是无常的。
- 常返性：如果不是暂返的就是常返的。
- 可约性：如果所有状态都是互通的，那么不可约。
- 遍历性：如果一个状态是非周期的并且是正向递归的，那么这个状态具有遍历性。
有限状态空间：