某曲线上的点到两点距离和最小的问题都可以用做椭圆解决

最新推荐文章于 2021-03-30 15:31:33 发布
最新推荐文章于 2021-03-30 15:31:33 发布
阅读量369 收藏
点赞数
CC 4.0 BY-SA版权
原文链接：http://www.cnblogs.com/yeluqing/archive/2012/10/07/3828253.html
本文探讨了求解两点到直线上一点的距离和最小值的经典几何问题。介绍了传统做法及利用椭圆特性求解的新思路，并解释了背后的数学原理。

先看一道中学里常见的题目，如图，

已知直线CD，直线CD一侧有两个点A,B.求CD上的一点P，使得|AP|+|BP|最小.

 

通常的做法是:如图，

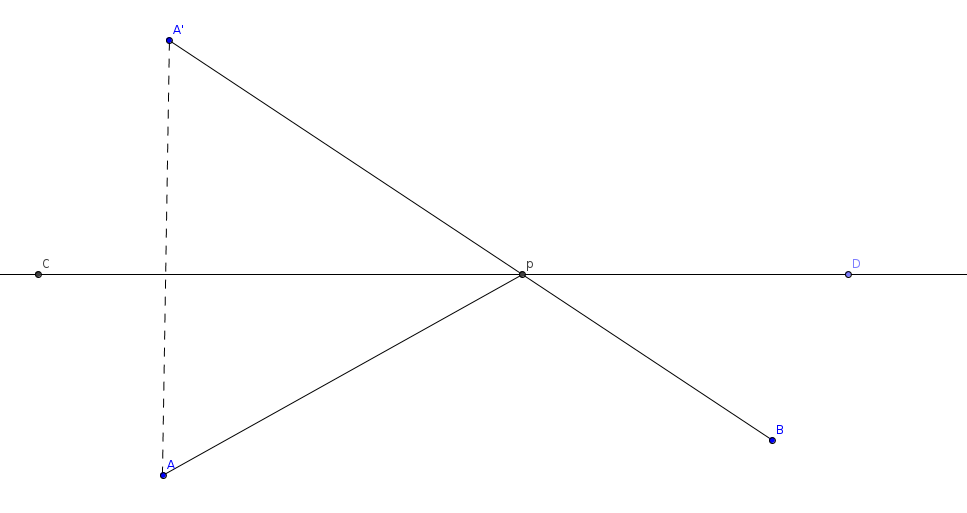
做点A关于CD的对称点A'.连接A‘B，与CD相交于P.则P点即为满足条件的点.这是因为，|AP|+|BP|=|A‘P|+|PB|=|A’B|.如果是直线CD上的其它除P外的点E的话，则AEB会形成一个三角形，由于三角形的两边之和大于第三边，即|AE|+|EB|>|A'B|,因此除去P外的其它点都不是满足条件的.

 

 

受我的博文两点到圆的最小距离的启发，我发现还有一种方法求满足条件的点P.方法如下:如图,

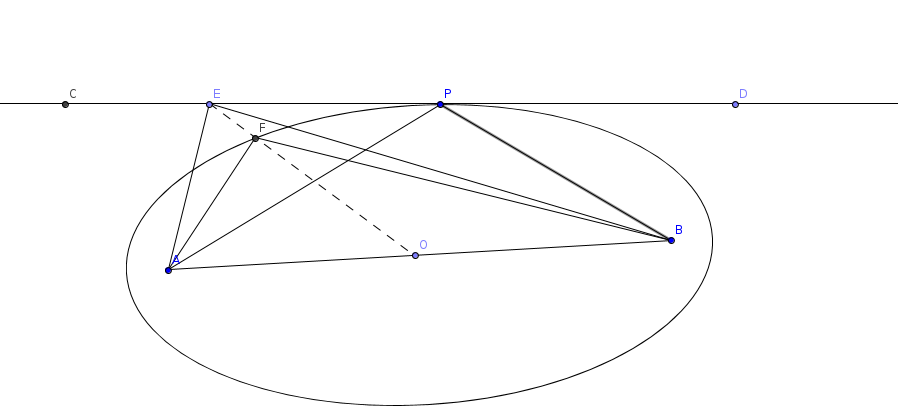
做以A,B为焦点的椭圆，且椭圆与直线CD相切于P，则切点P即为满足条件的点.至于为什么，请读者参考我的博文两点到圆的最小距离 ,两者的论证过程是完全一样的.

 

由此可见，求某曲线上的点到两点距离和最小的问题都可以用做椭圆解决.

转载于:https://www.cnblogs.com/yeluqing/archive/2012/10/07/3828253.html

matlab点到曲线的距离视频,在MATLAB中找到点与曲线之间的最小距离
weixin_28744601的博客
03-16 1917
小智..5当有人说“它很复杂”时，答案也总是很复杂，因为我不知道您到底拥有什么。因此，我将介绍一些基本思想。如果曲线是已知的非线性函数，则使用符号工具箱开始。例如，考虑函数y = x ^ 3-3 * x + 5，并且在x，y平面上的点(x0，y0)=(4,3)。写下距离的平方。欧几里得距离很容易写。(x - x0)^2 + (y - y0)^2 = (x - 4)^2 + (x^3 - 3*x +...
python寻找距离最近的点_python – 找到从点到复杂曲线的最小距离
weixin_39967405的博客
12-03 1409
如果您开放使用图书馆,请查看：https://github.com/Toblerity/Shapely作为一个快速的例子(points.txt包含你在你的问题链接的数据)：import shapely.geometry as geomimport numpy as npcoords = np.loadtxt('points.txt')line = geom.LineString(coords)po...
距离之和最小
xbgdzj的博客
02-24 5095
距离之和最小 Description X轴上有N个点，求X轴上一点使它到这N个点的距离之和最小，输出这个最小的距离之和。 Input 第1行：点的数量N。(2 <= N <= 10000) 第2 - N + 1行：点的位置。（-10^9 <= Pii <= 10^9) Output 输出最小距离之和 Sample Input ...
hdu 6097 Mindis（圆上一点到圆内(距圆心相等的)两点的距离和最短）
Darkarts
08-12 5121
Mindis题目链接：Mindis题意：圆内或者圆周上有两个点pp和qq，圆心为oo，并且op=oqop=oq，让你在圆上找一点dd，使得dp+dqdp+dq最小官方题解： 为什么是中垂线上的点取得最小值？ 个人理解应该是类似于这种情况吧，不过任谁做这道题时首先想到的应该都是中垂线吧。。 还有就是极端情况，做出反演点（什么是反演点）如果直线p′q′p'q'与圆有交点，则答案为两点间距离 否则
点到椭圆的最短距离
stereohomology
09-02 8748
Minimum Distance to an EllipseDate: 06/10/99 at 11:18:23 From: Christian Gauthier Subject: Geometry Conic EllipseWhat is the minimum distance between a point inside or outside an ellipse and the el
经典算法 | 给定数轴上点，寻找一个点到其他点的距离之和最小
u012737193的博客
01-13 2万+
给你一个数轴上的许多个点，让你寻找一个点A，使得A到其他所有数轴上的点的距离之和最短  毫无疑问，当数轴上的点的数量是偶数的时候，A取在数轴上所有点按照其坐标排列，排在最中间的两个点中间，  当数轴上的点的数量是奇数的时候，A取这些所有点按照其坐标排列，排在最中间的点 当取好A之后求所有点到其距离之和即可   代码如下 class Solution { public: int m
将一组点投影到椭圆上，并返回椭圆上最近的对应点Matlab代码.rar
01-08
在数学和计算机科学领域，特别是在图像处理、数据分析和计算机图形学中，将一组点投影到椭圆上并返回椭圆上最近的对应点是一个常见的问题。这个问题的解决对于许多应用至关重要，比如物体边界提取、路径优化和模式...
matlab求椭圆的弧长,用MATLAB实现求椭球上任意两点的最短弧长
weixin_42466331的博客
03-17 2560
基于法向矢量导向的求椭球上两点的最短弧长问题分析求椭球上任意两点间的最短弧长用数学来推算解析解的话十分复杂，因此考虑通过使用计算机来近似求解。问题的难点在于怎样让每一步都是处在最优的状态，以及怎样使每一步的方向都尽量处在该点能够选择的最优方向上。求椭球上两点的最短路，很容易想到用传统的最短路算法如迪杰斯特拉算法或弗洛伊德算法求解，但是在椭球将步长离散化后，构造以及运用邻接矩阵十分复杂，在保证一定精...
距两点距离之比恒定点的轨迹
TMS_LI的专栏
03-30 4022
距两点距离之比恒定点的轨迹 问题 到两点的距离之和不变的点轨迹是椭圆，到两点距离之差不变的点轨迹是又曲线，那么到两点距离之比不变点的轨迹是什么呢？ 由于角平分线的特性，问题可以这样描述： AB之间有一点D，在AB之外找一点C，所得CD是∠ACB\angle{ACB}∠ACB的角平分线，求C的轨迹。 三角形两腰的比例为：ACBC=ADDB\frac{AC}{BC} = \frac{AD}{DB}BCAC​=DBAD​ 而这个比例固定，容易用解析几何的方法求出C的轨迹方程。结果是一个圆。 这里使用几何的方法证
点到曲线的距离
lcydhr的专栏
05-27 1万+
1、正交   正交是直观概念中垂直的推广，如果两个向量正交，则这两个向量垂直，其点乘为0. 2、点到隐曲线的距离   假设点坐标为（dx,dy）, 曲线方程为f(x,y)=0, 从隐曲线最近点（u,v）到该点的向量必垂直于曲线，因此可以通过寻找满足下式的点获得最近点：                       1)（u，v）是曲线上的一点，满足f(u,v)=0；  
数轴上一个点到其他点距离之和最小问题
wyg1997
03-24 8211
这是一类问题，好多题要用到这个知识。 问题让求数轴上的一个点到其他点的距离之和，使这个和最小。 当然这里可以用 [-sum,sum] 来枚举求解，但是这里有更简单的方法，就是取这些点的中位数。
过椭圆外一点引两条切线方程_椭圆外一点引椭圆的两条切线互相垂直问题巧解 -...
weixin_39915505的博客
12-30 2588
椭圆外一点引椭圆的两条切线互相垂直问题巧解x2y2 问题： 已知椭圆c: 2?2?1(a?b?0)，点P(x0 ，y0)是椭圆外一点，且由点P引椭ab圆的两条切线互相垂直，则点P(x0，y0)的轨迹方程为解：设两切点为A(x1，y1)，B(x2，y2)，则pA?PB?0,即：(x1-x0)(x2-x0)+(y1-y0)(y2-y0)=022所以，x1x2?x0(x1?x2)?x0?y1y2?(y1...
椭圆公式
热门推荐
mjiansun的专栏
10-17 3万+
第一定义 平面内与两定点  、  的距离的和等于常数  （  ）的动点的轨迹叫做椭圆。 即： 其中两定点  、  叫做椭圆的焦点，两焦点的距离  叫做椭圆的焦距。  为椭圆的动点。 椭圆截与两焦点连线重合的直线所得的弦为长轴，长为 。 椭圆截垂直平分两焦点连线的直线所得弦为短轴，长为   。 可变为   第二定义 椭圆平面内到定点 （c，0）的距离和到定直线 ：  （  不在 ...
如何求曲线上任意点到端点的距离
nj198624的专栏
11-08 2089
现在在网上找到了一段代码，利用它可以求曲线上任意点到端点的距离，应该可以满足求曲线上任意两点沿曲线的距离的要求，大家可以看一下，希望能提出宝贵的意见 具体做法如下： 1、在ARCMAP中加载点图层和对应的线图层，注意只能加载这两个图层，且点图层必须在线图层之上，为了便于大家更清楚地看清起点，我把符号改为指向末端的方向箭头 2、在点图层属性表中新加到端点的字段如aa，类型为double，如
线上到指定点的距离最短的一点
weixin_34353714的博客
05-29 354
在ArcEngine中可以通过两种方式实现： 第一种：由ICurve和IPolyline接口的QueryPointAndDistance方法实现。              该方法中有七个参数，下面对这些参数进行详细说明：           1.extension参数：esriSegmentExtension枚举类型，用于指定曲线段延伸的方式，主要有esriNoExtension（曲线段不...
两点到圆的最小距离
weixin_34166472的博客
10-02 1010
有人在哆嗒网提了一道问题.我觉得挺有意思.问题如下:有一动点在圆$(x+a)^2+(y+b)^2=c^2,c>0$上运动，圆外有两点$C(d,e),D(f,g)$，两点到动点的距离之和最小，求此时动点的坐标. 如图. 解决方案如下:当线段CD与圆不相交时， 做以C,D为焦点，且与圆相切的椭圆.椭圆与圆的切点即为满足条件的点.这是因为，若不然，如图，...
点到曲线最短距离
最新发布
07-02
<think>我们正在讨论如何计算点到曲线的最短距离。根据引用[^1]和引用[^2]，我们可以采用穷举法（即枚举曲线上的点）或者利用优化算法（如梯度下降）来求解。然而，对于解析表达式已知的曲线，我们可以使用微积分的方法，通过求解导数为零的点来找到最短距离。设曲线为$y=f(x)$，点为$(x_0,y_0)$。则点到曲线上任一点$(x,f(x))$的距离为： $$d =\sqrt{(x-x_0)^2+ (f(x)-y_0)^2}$$为了简化计算，我们通常最小化距离的平方： $$s(x) =(x-x_0)^2 +(f(x)-y_0)^2$$然后求$s(x)$的最小值。这可以通过求导并令导数为零：$$s'(x) =2(x-x_0) +2(f(x)-y_0)f'(x)=0$$即： $$(x-x_0)+ (f(x)-y_0)f'(x)=0$$这是一个关于$x$的方程，解这个方程得到候选点，然后比较这些候选点以及曲线端点处的距离，即可得到最短距离。但是，如果曲线是由参数方程给出，例如$x=g(t),y=h(t)$，则距离平方函数为：$$s(t)= (g(t)-x_0)^2 +(h(t)-y_0)^2$$求导：$$s'(t) =2(g(t)-x_0)g'(t)+2(h(t)-y_0)h'(t)=0$$即： $$(g(t)-x_0)g'(t) +(h(t)-y_0)h'(t)=0$$同样需要解这个关于$t$的方程。然而，解析解往往难以求得，因此在实际应用中，我们常采用数值方法。例如，可以使用梯度下降法、牛顿迭代法或者直接使用优化库。另外，引用[^2]提到，如果曲线是离散点集，那么我们可以使用穷举法（即计算点到每个离散点的距离）或者更高效的方法如KD树来加速搜索。引用[^3]提到Hough变换可以用于检测直线和曲线，但这里我们关注的是点到曲线的最短距离，所以Hough变换可能不直接适用。引用[^4]给出了一个计算两个经纬度点之间距离的公式（大圆距离），这适用于地球表面上的点，但同样不直接适用于一般曲线。因此，针对点到曲线的最短距离计算，我们可以总结如下：1.如果曲线有解析表达式且可导，则通过求解方程（导数等于零）得到候选点，然后比较这些点处的距离。2.如果曲线由参数方程给出，同样通过求解导数等于零的方程（关于参数的方程）得到候选点。3.如果曲线是离散点集，则使用穷举法（或者用KD树优化）计算点到每个点的距离，取最小值。4.如果曲线是连续的但难以解析求解，则使用数值优化方法（如梯度下降、牛顿法）来最小化距离函数。下面我们给出一个使用数值方法求解的示例（使用MATLAB的fminsearch函数）：假设曲线为$y=x^2$，点为$(1,3)$，我们求点到曲线的最短距离。步骤：1.定义距离平方函数：s=@(x)(x-1).^2 +(x.^2-3).^2;2.使用fminsearch寻找最小值点：x_min= fminsearch(s,0); （0是初始猜测值）3.计算最小距离：d_min =sqrt(s(x_min));注意：由于fminsearch寻找的是局部最小值，所以初始猜测值很重要，可能需要尝试多个初始值。对于离散点集，我们可以使用以下MATLAB代码（假设曲线点集为P，点为Q）：distances= sqrt(sum((P -Q).^2,2)); %计算Q到P中每点的距离min_distance =min(distances);如果点集很大，考虑使用KDTree加速：kdtree= KDTreeSearcher(P);[idx, min_distance]= knnsearch(kdtree,Q);在Python中，我们可以使用scipy的优化函数或scikit-learn的KDTree。因此，具体方法的选择取决于曲线的表示形式（解析式、参数式、离散点）以及是否可导。最后，需要注意的是，当曲线比较复杂（比如有多个局部最小值）时，可能需要全局优化算法或者多个初始点尝试。相关问题：1.如何计算点到直线的最短距离？（直线是特殊的曲线，有解析公式）2.如何计算点到多段线（由多条线段组成）的最短距离？3.如何计算点到封闭曲线（如圆、椭圆）的最短距离？4.在三维空间中，如何计算点到空间曲线的最短距离？5.当曲线由隐式方程给出（如F(x,y)=0）时，如何计算点到曲线的最短距离？希望这些信息对你有帮助。</think>### 点到曲线最短距离计算方法 点到曲线的最短距离计算核心是**寻找曲线上离给定点最近的点的位置**。根据曲线表示形式（函数方程、参数方程、离散点）和需求精度，主要方法如下： #### 一、解析法（适用于可导函数） 若曲线为显函数 $y=f(x)$，给定点 $P(x_0,y_0)$： 1. **距离函数**：点到曲线的距离平方为 $$s(x) = (x - x_0)^2 + (f(x) - y_0)^2$$ 2. **求导归零**：最小距离需满足 $$\frac{ds}{dx} = 2(x - x_0) + 2(f(x) - y_0)f'(x) = 0$$ 3. **解方程**：求解非线性方程 $(x - x_0) + (f(x) - y_0)f'(x) = 0$ 的根，验证后取最小值点[^1]。 > **示例**：点 $P(1,2)$ 到曲线 $y=x^2$ > 解方程：$(x-1) + (x^2-2) \cdot 2x = 0$ → $2x^3 - 3x -1=0$ > 得实根 $x≈1.618$，最短距离 $d=\sqrt{(1.618-1)^2+(2.618-2)^2}≈1.249$ #### 二、数值优化法（通用方法） 当解析解困难时（如复杂函数或离散点）： 1. **梯度下降法**：沿距离函数的负梯度方向迭代搜索 $$x_{n+1} = x_n - \alpha \nabla s(x_n)$$ 2. **牛顿法**：利用二阶导数加速收敛 $$x_{n+1} = x_n - \frac{s'(x_n)}{s''(x_n)}$$ 3. **MATLAB/Python工具**： ```matlab % MATLAB 示例 f = @(x) x.^2; % 曲线函数 dist_func = @(x) (x-1).^2 + (f(x)-2).^2; % 距离函数 x_min = fminsearch(dist_func, 0); % 数值优化 ``` #### 三、离散点曲线处理 若曲线由点集 $\{Q_i(x_i,y_i)\}$ 表示： 1. **穷举法**：计算点到所有 $Q_i$ 的欧氏距离 $$d_i = \sqrt{(x_i-x_0)^2 + (y_i-y_0)^2}$$ 取 $d_{\text{min}} = \min\{d_i\}$（适用于少量点）[^1] 2. **KD-Tree加速**：对海量点预处理空间索引，快速近邻搜索（复杂度 $O(\log n)$） ```python # Python 示例 from sklearn.neighbors import KDTree points = np.array([[x1,y1], [x2,y2], ...]) # 曲线点集 kdtree = KDTree(points) d_min, idx = kdtree.query([[x0, y0]], k=1) # 返回最近距离和索引 ``` #### 四、特殊曲线场景 1. **参数方程曲线** $x=g(t), y=h(t)$： 最小化 $s(t)=(g(t)-x_0)^2 + (h(t)-y_0)^2$，求 $\frac{ds}{dt}=0$ 2. **空间曲线**：将二维方法扩展到三维坐标 3. **大圆距离**（地球表面）：用Haversine公式计算经纬度距离[^4] $$a = \sin^2(\Delta\phi/2) + \cos\phi_1\cos\phi_2\sin^2(\Delta\lambda/2)$$ $$d = 2R \cdot \atan2(\sqrt{a}, \sqrt{1-a})$$ #### 注意事项 1. **多极值点**：曲线复杂时需多次迭代避免陷入局部最优解[^2] 2. **不可导点**：分段处理（如折线在顶点处单独计算） 3. **精度权衡**：数值法需平衡计算效率与精度要求 --- ### 相关问题 1. **如何高效计算点到三维空间曲线的最短距离？** 2. **当曲线由隐函数 $F(x,y)=0$ 表示时，最短距离如何求解？** 3. **离散点曲线简化（如Ramer-Douglas-Peucker算法）对距离计算精度有何影响？** 4. **如何利用Hough变换检测直线/圆并计算点到它们的距离？**[^3] [^1]: 穷举法通过枚举曲线上的所有点对计算距离，适用于离散点曲线。 [^2]: 对于噪声或不可微曲线，需选择在平滑近似或插值曲线上计算距离。 [^3]: Hough变换可检测图像中的直线和圆等几何形状。 [^4]: 大圆距离公式适用于地球表面两点间的最短路径计算。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值