统计学概念基础---数学期望,方差,标准差,协方差，自协方差，自相关

2019独角兽企业重金招聘Python工程师标准>>>

1.基本概念

数学期望就是平均值:

均值公式：

标准差：

方差：

均值描述的是样本集合的中间点，它告诉我们的信息是有限的，而标准差给我们描述的是样本集合的各个样本点到均值的距离之平均。

2.协方差

 

二、为什么需要协方差

 

标准差和方差一般是用来描述一维数据的，但现实生活中我们常常会遇到含有多维数据的数据集，最简单的是大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解更多，比如，一个男孩子的猥琐程度跟他受女孩子的欢迎程度是否存在一些联系。协方差就是这样一种用来度量两个随机变量关系的统计量，我们可以仿照方差的定义：

来度量各个维度偏离其均值的程度，协方差可以这样来定义：

协方差的结果有什么意义呢？如果结果为正值，则说明两者是正相关的（从协方差可以引出“相关系数”的定义），也就是说一个人越猥琐越受女孩欢迎。如果结果为负值， 就说明两者是负相关，越猥琐女孩子越讨厌。如果为0，则两者之间没有关系，猥琐不猥琐和女孩子喜不喜欢之间没有关联，就是统计上说的“相互独立”。

从协方差的定义上我们也可以看出一些显而易见的性质，如：

 

三、协方差矩阵

前面提到的猥琐和受欢迎的问题是典型的二维问题，而协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算个协方差，那自然而然我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

这个定义还是很容易理解的，我们可以举一个三维的例子，假设数据集有三个维度，则协方差矩阵为：

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度的方差。

 

理解协方差矩阵的关键就在于牢记它的计算是不同维度之间的协方差，而不是不同样本之间。拿到一个样本矩阵，最先要明确的就是一行是一个样本还是一个维度，心中明确整个计算过程就会顺流而下，这么一来就不会迷茫了。

四 自协方差与自相关函数

在给出自相关函数定义之前先介绍自协方差函数概念。随机过程 {xt} 中的每一个元素xt，t = 1, 2, … 都是随机变量。对于平稳的随机过程，其期望为常数。这里用 m 表示，即

    E(xt) = m , t = 1, 2, …                     (10.27)

随机过程的取值将以 m 为中心上下变动。平稳随机过程的方差也是一个常量。

    

s x2用来度量随机过程中变量取值对其均值 m 的离散程度。

相隔k期的两个随机变量xt 与xt+k 的协方差，即滞后k期的自协方差，定义为

    

自协方差序列

    gk , k = 0, 1, …, K,                               (10.30)

称为随机过程 {xt} 的自协方差函数。当k = 0 时，

    

自协方差 g k是有量纲的，它的测量单位与变量的测量单位有关。为消除量纲，给出更方便的自相关系数定义，

    

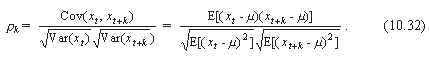
rk是无量纲的。

因为对于一个平稳过程有

Var(xt) = Var(xt+k) = sx2

所以上式可以改写为

    

由于 g 0 = sx2，上式可表示为

    

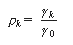
当 k = 0 时，有 r0 = 1。

以滞后期k为变量的自相关系数列

    rk , k = 0, 1, …, K                               (10.34)

称为自相关函数。因为 rk = r-k ，自相关函数是以零为对称的，所以实际研究中只需给出自相关函数的正半部分即可。

自相关函数是随机变量与其滞后变量的相关系数列，用以考察随机变量与其滞后变量的相关强度

转载于:https://my.oschina.net/zhiyonghe/blog/979311