三维空间两直线/线段最短距离、线段计算算法

最新推荐文章于 2023-10-24 09:18:14 发布

转载

最新推荐文章于 2023-10-24 09:18:14 发布 · 2.7k 阅读

5 ·

CC 4.0 BY-SA版权

原文链接：https://segmentfault.com/a/1190000006111226

文章标签：

#matlab #ux #c#

本文介绍了计算三维空间中两线段最短距离的算法，通过向量表示法建立数学模型，并推导出求解s_c、t_c的公式。当线段不平行时，使用公式求解最近点；若平行，则通过特定方式计算固定点距离。最后给出了C#实现代码。

设有两空间线段

$L_s$，其起点、终点坐标为$ s_0、s_1 $，方向向量$\vec u = s_1-s_0 $
$L_t$，其起点、终点坐标为$ t_0、t_1 $，方向向量$\vec v = t_1-t_0 $
记两线段对应的直线为$l_s、l_t$，采用向量表示法如下：

$$l_s = s_0+c_s\cdot\vec u$$
$$l_t = t_0+c_t\cdot\vec v$$
当$0\le c_s、c_t\le1$时，上述两式表达
设最短距离两点分别为$s_j$、$t_j$，则有
$$s_j = s_0+s_c\cdot\vec u$$
$$t_j = t_0+s_c\cdot\vec v$$
其中$s_c$、$t_c$为$s_j$、$t_j$两点所对应的标量。

记向量$\vec w$=$s_j-t_j$，记向量$\vec w_0$=$s_0-t_0$，根据下图可以得出：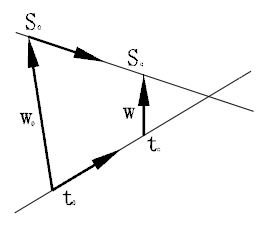
图片描述
$$\vec w=s_0+s_c\cdot\vec u-(t_0+t_c\cdot\vec v)$$ 即：
$$\vec w=\vec w_0+s_c\cdot\vec u-t_c\cdot\vec v\qquad(公式1)$$
如果$s、t$两条直线不平行、重合，则存在唯一的两点$s_c、t_c$使线段$\overrightarrow {s_ct_c}$为$l_s、l_t$最近两点的连线。同时，线段$\overrightarrow {s_ct_c}$也是唯一与两条直线同时垂直的线段。转换为向量表达即为：
$$\vec u\cdot\vec w=0\qquad\vec v\cdot\vec w=0$$