icp算法基本思想

Icp基本思想参考资料：http://www.cnblogs.com/jian-li/articles/4945676.html ，包括点-点，点-面的各种icp变种

Icp算法就是两个点云X、Y之间的匹配，最小化均方误差

其中R是旋转矩阵，t是平移矩阵。

方法：

 

 

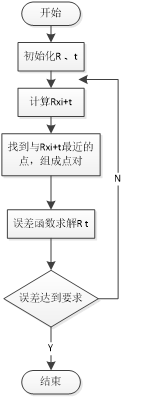
搜索策略

 

找到最近点，使用kd-tree，参考资料

http://www.cnblogs.com/xy123001/p/5831116.html

http://blog.sina.com.cn/s/blog_6f611c300101bysf.html

 

 

误差函数求解

常见的：基于奇异值分解的方法、四元数方法。

 

其他参考：

mrpt的icp

http://www.mrpt.org/Iterative_Closest_Point_%28ICP%29_and_other_matching_algorithms

 

 

 

 

用kd-tree来找最近点，是整个icp算法中最耗时的部分。所以，如果点云密集，就要下采样，下采样默认5

 

通过ini配置文件，还可以选择icp算法的种类，是经典算法还是LM算法，

经典算法和LM算法的区别就是 经典算法使用的最小二乘法，替换成了LM算法中的非线性最小二乘。

LM加大了计算量。

 

ICPfastSlam算法

 

Icp+粒子滤波

祝继华, 郑南宁, 袁泽剑,等. 基于ICP算法和粒子滤波的未知环境地图创建[J]. 自动化学报, 2009, 35(8):1107-1113.

 

 

点-平面

下图是点-切平面距离的示意图

 

 

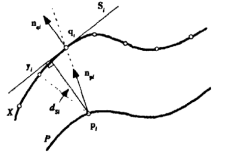
与点到点的ICP算法相比，运用点到平面的距离的方法大大减少了计算量以及迭代次数，但是该方法的鲁棒性并不是太好。

 

由icp迭代后的点求机器人位姿

 

举个例子。

下图中有两个坐标系A 和 B

B是由A经过平移和旋转得到的。平移矩阵为R，旋转矩阵T

A旋转sita= - 90度（逆时针为正），沿A的x轴平移3之后，得到了B坐标系。

R=[0,1; -1,0]   T=[3, 0]

M=[R T;0 1]

 

一个点在A下为[1;5],在B下为[-5;-2]

M*[-5;2] = [1;5]

Inv(M)*[1 ;5] = [-5;-2]

 

由此可知，激光扫描到的点，经过icp匹配之后，R 、t就已经得到了，sita tx ty也就知道了，这就相当于 机器人就是坐标原点。

 

转载于:https://www.cnblogs.com/xy123001/p/5844809.html