统计学习方法(李航)
第1章 统计学习方法概论
1.2监督学习
1、统计学习包括监督学习、非监督学习、半监督学习、强化学习。统计学习方法这本书主要讨论监督学习。
2、监督学习(supervised learning)的任务:学习一个模型,使得模型能够对任意给定的输入,对其相应的输出做出一个好的预测。
3、基本概念
(1)输入空间(input space):在监督学习中,所有可能输入的值的集合。
(2)输出空间(output space):在监督学习中,所有可能的输出的集合。
(3)特征空间(feature space):所有特征向量存在的空间。特征空间的每一维对应于一个特征。
(4)实例(instance):每个具体的输入。通常实例由特征向量表示。输入实例x的特征向量记作:
其中,x(i)是x的第i个特征。
监督学习从训练数据(training data)集合中学习模型,对测试数据(test data) 进行预测。训练数据由输入(或特征向量)与输出对组成,训练集通常表示为:
![]()
测试数据也由相应的输入与输出对组成。输入与输出对又称为样本(sample)或样本点。
(5)假设空间(hypothesis space):模型属于由输入空间到输出空间的映射的集合,这个集合就是假设空间。假设空间的确定意味着学习范围的确定。
4、输入变量与输出变量均为连续变量的预测问题为回归问题;输出变量为有限个离散变量的预测问题称为分类问题;输入变量与输出变量均为变量序列的预测问题称为标注问题。
1.3 统计学习三要素
统计学习方法由模型、策略和算法构成。
1.3.1 模型
1、模型就是所要学习的条件概率分布P(Y|X)或决策函数Y=f(x)。假设空间用![]() 表示。
表示。
(1)假设空间可以定义为决策函数的集合:
![]()
其中,X和Y是定义在输入空间![]() 和输出空间
和输出空间![]() 上的变量。
上的变量。![]() 通常是由一个参数向量θ决定的函数族:
通常是由一个参数向量θ决定的函数族:
![]()
参数向量θ取之于n维欧式空间Rn,称为参数空间。
(2)假设空间也可以定义为条件概率的集合:
![]()
其中,X和Y是定义在输入空间![]() 和输出空间
和输出空间![]() 上的随机变量。
上的随机变量。![]() 通常是由一个参数向量θ决定的条件概率分布族:
通常是由一个参数向量θ决定的条件概率分布族:
![]()
2、由决策函数表示的模型可以称为非概率模型,由条件概率表示的模型为概率模型。
1.3.2 策略
1、概念
(1)损失函数:度量模型一次预测的好坏。
(2)风险函数:度量平均意义下模型预测的好坏。
2、有了模型的假设空间后,接着需要考虑应该按照什么样的准则学习或选择最优的模型。
3、损失函数是f(X)和Y的非负实值函数,记作L(Y,f(x))。其中,f(X)是根据输入X得到的,是一个预测值。Y是真实值。损失函数值越小,模型就越好。
统计学习常用的损失函数有:
(1)0-1损失函数(0-1 loss function)
![]()
(2)平方损失函数(quadratic loss function)
![]()
(3)绝对损失函数(absolute loss function)
![]()
(4)对数损失函数(logarithmic loss function)或对数似然损失函数(log-likelihood loss function)
![]()
损失函数的期望是:![]() 。这是理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失,称为风险函数(risk function)。
。这是理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失,称为风险函数(risk function)。
经验风险:![]() 在假设空间、损失函数和训练数据集确定的情况下,该函数式就可以确定。
在假设空间、损失函数和训练数据集确定的情况下,该函数式就可以确定。
Remp(f)是模型f(X)关于训练数据集的平均损失。而Rexp(f)是模型关于联合分布的期望损失。当样本容量N趋于无穷,Remp(f)趋于Rexp(f)。所以理论上可以用经验风险估计期望风险,但在实际中,由于训练样本数量有限,往往行不通。由此对经验风险进行矫正,出现了两个基本策略:经验风险最小化和结构风险最小化。
4、关于经验风险最小化和结构风险最小化。
(1)经验风险最小化(empirical risk minimization,ERM)认为:经验风险最小的模型就是最优的模型,其实就是求解最优化问题:
![]()
当样本容量足够大时,可以保证有很好的学习效果,在现实中被广泛采用。例如:极大似然估计(maximum likelihood estimation)就是经验风险最小化的例子。当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化就是极大似然估计。
缺点:样本量很小时,经验风险最小化的学习效果不一定好,会产生“过拟合”现象。
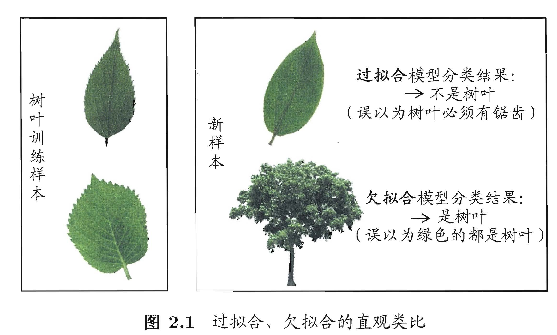
通常,欠拟合比较容易克服,例如:在决策树学习中扩展分支,在神经网络学习中增加训练轮数等。而过拟合则很麻烦,过拟合时机器学习面临的关键障碍,是无法彻底避免的,能做的只是“缓解”。
(2)结果风险最小化(structural risk minimization,SRM):是为了防止过拟合而提出的。结构风险最小化等价于正则化。
在假设空间、是你是函数和训练数据集确定的情况下,结构风险的定义是![]() ,结构风险是在经验风险上加上表示模型复杂度的正则化项或罚项。其中J(f)为模型的复杂度,模型越复杂,复杂度J(f)越大,反之越小。
,结构风险是在经验风险上加上表示模型复杂度的正则化项或罚项。其中J(f)为模型的复杂度,模型越复杂,复杂度J(f)越大,反之越小。
结构风险最小化的例子:贝叶斯估计中的最大后验概率估计(maximum posterior probability estimation,MAP)。当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化等价于最大后验概率估计。
结构风险最小化就是求解最优化问题:
![]()
这样,监督学习就变成了经验风险或结构风险函数的最优化问题。
1.3.3 算法
算法指学习模型的具体计算方法,也就是用什么样的计算方法求解最优模型。
1.4 模型评估与模型选择
1.4.1训练误差与测试误差
1、当损失函数给定时,基于损失函数的模型的训练误差(training error)和模型的测试误差(test error)就成为学习方法评估的标准。需要注意的是:统计学习方法中具体采用的损失函数未必是评估时使用的损失函数。







 本文介绍了监督学习的基本概念,包括输入空间、输出空间、特征空间等,并详细解释了统计学习的三要素:模型、策略和算法。同时探讨了模型评估与选择的方法。
本文介绍了监督学习的基本概念,包括输入空间、输出空间、特征空间等,并详细解释了统计学习的三要素:模型、策略和算法。同时探讨了模型评估与选择的方法。
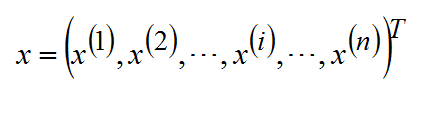
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








