计算圆周率π和显示进度条

最新推荐文章于 2024-11-09 10:22:04 发布

转载最新推荐文章于 2024-11-09 10:22:04 发布 · 188 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/xiayiLL/p/10569161.html

博客介绍了π的来历，它是圆的周长和直径之比，由琼斯首次使用，欧拉推广。还阐述了π的计算方法，如Wallis公式法和蒙特卡罗方法，并尝试代码实现，不过Wallis公式法因算法不熟悉无法正确输出，蒙特卡罗方法运行完成约需104s。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

π的计算

1.π的来历

π即圆周率，定义为：园的周长和直径之比，是一个常数。通常用希腊字母π来表示。π=3.14159265.....，通常用π=3.14进行计算。英国人琼斯在1706年首次使用π，代表圆周率，但是没有被采用，后来，欧拉予以提倡，才渐渐被推广开来。此后π成为圆周率的专用符号。π的历史是饶有趣味的。对于π的研究程度，在一定程度上反映一个地区和时代的数学水平。

2.π的计算方法

法1：Wallis公式的计算方法（沃利斯公式）

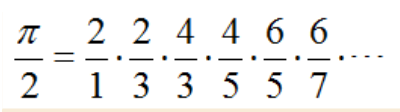
法2：蒙特卡罗方法（抛点法）

3.代码实现

法1：Wallis公式的计算方法（沃利斯公式）

 1 from time import perf_counter   
 2 def Dt(i):         
 3     N = pow(10,p)
 4     a = int((i/N)*50)
 5     b = 50 - a
 6     Y , N = '*' * a , '.' * b
 7     print("\r计算中：{:3.0f}% [{}->{}] {:.2f}s".format(2*a,Y,N,perf_counter()),end='')
 8 
 9 p = eval(input('计算Pi精确到小数点后几位数：'))
10 print('\n{:^70}'.format('计算开始'))
11 a,b,pi,chu,i,j=2,3,1,2,1,0
12 perf_counter()
13 while (i<=50000):     
14     chu=a/b
15     pi*=chu
16     i+=1
17     if i%2==0:
18         a+=2
19     else:
20         b+=2
21     Dt(j)
22 print('\n{:=^70}'.format('计算完成'))
23 print('\nPi的计算值为：{}'.format(round(pi*4,p)))

注：由于该算法并不熟悉，无法使其正确输出（循环停止的条件无法确定）

法2：蒙特卡罗方法（抛点法）

 1 from random import random
 2 from math import sqrt
 3 from time import perf_counter
 4 DARTS=100000000
 5 hits=0.0
 6 b=1
 7 perf_counter()
 8 for i in range(1,DARTS+1):
 9     x,y=random(),random()
10     dist=sqrt(x**2+y**2)
11     if dist<=1.0:
12         hits=hits+1
13     if i== DARTS*0.01*b :      
14         print("\r%{} [{}->{}]".format(b,'*'*b,'-'*(10-b)),end="")
15         b+=1
16 pi = 4* (hits/DARTS)
17 print("\nPi=={:.7f}".format(pi))
18 print("运行时间为:{:.5f}s".format(perf_counter()))

4.结果显示

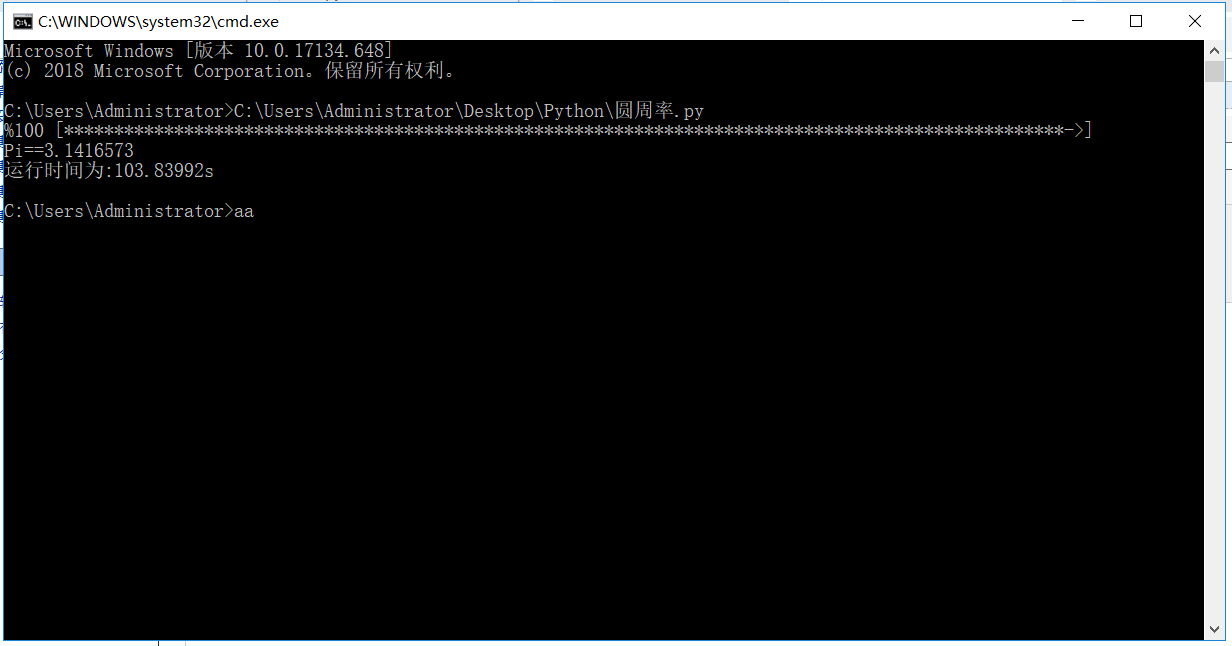
由图知：运行完成需要接近104s的时间

转载于:https://www.cnblogs.com/xiayiLL/p/10569161.html